测算数据离散程度的方差及其重要性

方差（variance）是在概率论和统计方差衡量随机变量或一组数据离散程度的度量。概率论中方差被用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是各个数据分别与其平均数之差的平方的和的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义。当数据分布比较分散（即数据在平均数附近波动较大）时，各个数据与平均数的差的平方和较大，方差就较大；当数据分布比较集中时，各个数据与平均数的差的平方和较小。因此方差越大，数据的波动越大；方差越小，数据的波动就越小。

样本中各数据与样本平均数的差的平方和的平均数叫作样本方差，样本方差的算术平方根叫作样本标准差。样本方差和样本标准差都是衡量一个样本波动大小的量，样本方差或样本标准差越大，样本数据的波动就越大。

方差和标准差是测算离散趋势最重要、最常用的指标。方差是各变量值与其均值离差平方的平均数，它是测算数值型数据离散程度的最重要的方法。标准差为方差的算术平方根，用S表示。方差相应的计算公式为：

其中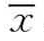表示样本的平均数，n表示样本的数量，xi表示个体，S2就表示方差。

标准差与方差不同的是，标准差和变量的计算单位相同，但在表现偏差时比方差清楚，因此我们分析时更多地使用的是标准差。

下面举一个电子商务实例：

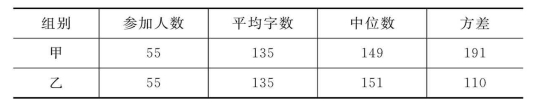
某农产品电子商务公司进行电脑汉字输入速度比赛，两个组参加比赛的选手每分钟输入汉字的个数，经统计和计算后结果如表3-1所示：(https://www.xing528.com)

表3-1　电脑汉字输入速度比赛结果统计表

有一位分析者根据表3-1得出如下结论：

①甲、乙两组选手的平均水平相同；

②乙组优秀的人数比甲组优秀的人数多（每分钟输入汉字达150个以上为优秀）；

③甲组选手比赛成绩的波动比乙组选手比赛成绩的波动大。

甲、乙的平均数相同，所以甲、乙两组选手的平均水平相同。根据中位数可知乙的中位数大，所以乙组优秀的人数比甲组优秀的人数多。根据方差数据可知，方差越大波动越大，反之越小，所以甲组选手比赛成绩的波动比乙组选手比赛成绩的波动大。要知道平均数和中位数反映的是数据的集中趋势，方差反映的是离散程度。