不同市场规模下三种模型运算结果比较

仍以算例“Test-184-4”为例，通过变化需求系数反应市场的规模。需求系数从0.4到10，表示的是市场需求规模是当前规模的0.4~10倍。小于系数0.4的市场规模产生的利润是负值应不安排航班，大于系数10的市场规模应考虑增加航班架次，所以这两者都不属于我们考察的范畴。假定市场竞争强度θ=0.5，表6-5记录了不同市场规模下三种不同模型BAFAM、CFAM、IDFAM的求解结果。这三种模型分别对应着θ=0、θ=0.5和θ=1。其中θ=0和θ=1下的“原始解”指的是直接求解BAFAM模型和IDFAM模型所得到的解，“实际收益”是指将上述求解结果作用于实际市场即θ=0.5时得到的实际收益。“时间”记录的是求解时间，以“秒”为单位。“Gap1”和“Gap2”分别是“原始解”和“实际解”的差值以及“实际收益”和“实际解”的差值，用百分比表示，即Gap1=（（原始解-实际解）/实际解）×100，Gap2=（（实际解-实际收益）/实际解）×100。

从表6-5可以看出，当市场规模较小的时候，BAFAM的Gap1和Gap2均明显高于IDFAM下的值，这是因为BAFAM假定所有的溢出需求会等比例地全部转移到其他替代品中去，所以航空公司会关闭一些价格较低的产品，以促使低价需求向高价需求转移，从而提高收益。但实际情况却是这些因低价票关闭而产生的溢出需求并没有按预期的全部转移，而是有更多的需求损失，导致实际收益的下降明显。这再次说明了BAFAM是对现实情况的过高估计，而且需求越少误差越大。在IDFAM和CFAM模型中，因为考虑到溢出需求会全部或大部分损失，所以在这两个模型中会开放部分低价票，以捕获全部需求，因此IDFAM下的Gap1和Gap2相对较小。但IDFAM假定所有的溢出需求全部损失，过于保守，开放了过多的低价票。随着需求的增多，BAFAM的Gap是不断减小，到需求足够大的时候，Gap2的值降为0。这是因为BAFAM一直在为高价票分配更多的座位，而当需求足够大时，BAFAM和CFAM的模型均只给最高价机票分配了同样的座位数，所以其收益是相等的。IDFAM的两个Gap值是随着需求的增加先增加后减小，直到为0。因为随着需求的增加，CFAM会选择关闭或给低价票分配较少的座位，期望低价需求向高价需求转移，以增加收益。而IDFAM则一直保持低价票开放直到高价需求达到座位容量，所以当需求在一定范围内增加时，IDFAM与CFAM的收益差会不断变大，但随着需求的越来越大，大到IDFAM最高价机票需求和座位容量相等时，它和CFAM能实现相同的期望收益。图6-8列出了三种模型在不同市场规模下的实际收益，从图中也能得到上述结论。

表6-5　不同市场规模下的结果比较

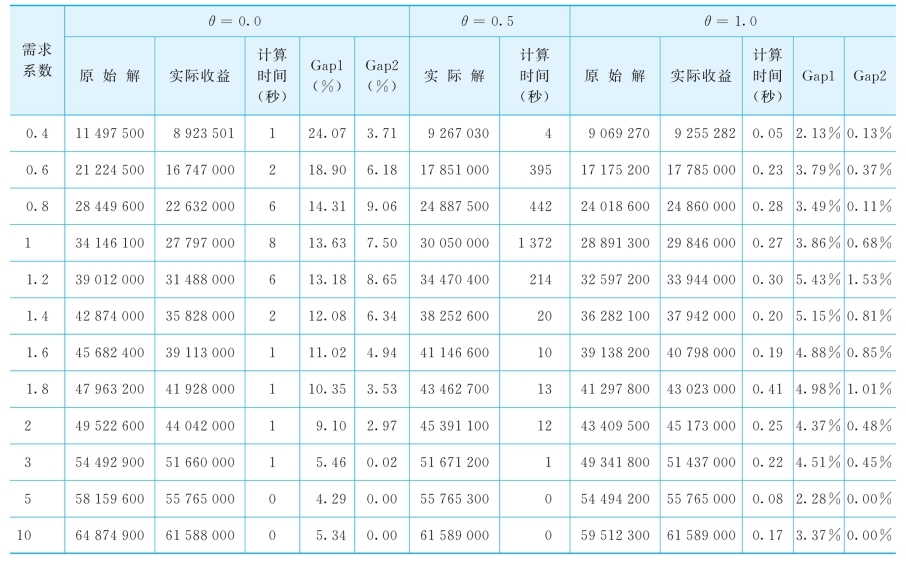
图6-8　不同市场规模下三类模型的实际收益比较

为了便于理解，下面给出一个简单的例子。(www.xing528.com)

例6.2 同例6.1一样，假设市场上有5个可替代的航空产品，分别用1，2，…，5表示，0表示不购买任何产品。vj的值是乘客对产品j的偏好。市场上竞争激烈，竞争系数θ=0.5。假设航班座位容量为C=20，各产品每售出一单位的期望收益如表6-6所示。

表6-6　可选产品集基本信息

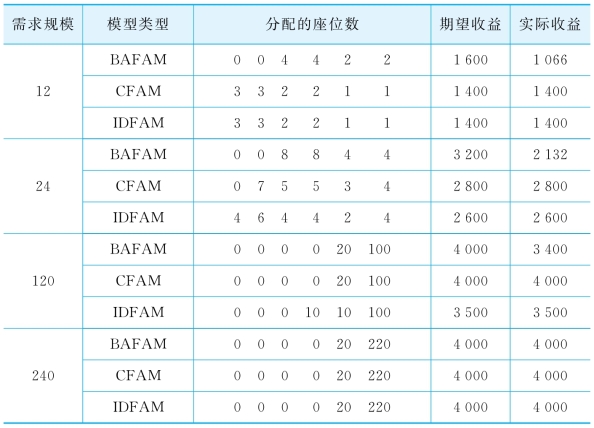
当需求D=12时，即D＜C，此时BAFAM的最优决策是关闭两个低价产品，则原来低价的6个需求分别有2个转移到3、4产品中，1个转移到5产品，损失1个，最大期望收益是1 600。而CFAM和IDFAM如果关闭低价票，则有更多的需求损失，且损失的收益大于转移的收益，故在这两种策略下的最优分配方案是开放所有的产品供乘客选择，且分配的座位数满足公式6-17，两种模型的最大期望收益均为1 400。当需求为D=24时，有部分需求溢出，此时CFAM会倾向向高价票提供较多的座位，BAFAM和CFAM的期望收益的差距在缩小，而IDFAM和CFAM的已经拉开差距。当需求为D=120时，BAFAM和CFAM均将座位分配给了最高价机票，两者的期望收益相等，而IDFAM和CFAM的期望收益差距进一步扩大。当需求为D=240时，最高价机票的原始需求大于等于C时，三者将所有的座位均分配给了最高价产品，所以获得了相同的收益，三者的差距为0（表6-7）。

表6-7　BAM、GAM和IDM三种模型下座位分配及收益的比较

上述例子证明了6.5.5中的结论。