不同竞争程度下的运算结果分析

对每一个基本算例，我们通过给定不同的θ值来反映市场的竞争程度：θ=0.0，0.3，0.5，0.7，1.0。

当θ=0时，意味着影子吸引力wj=θvj=0，即竞争企业的产品对产品j的用户的吸引力为0。这说明从产品j溢出的需求并不会转移到竞争对手提供的产品中去，而是全部转移到本公司提供的其他产品中去（包括不购买选项）。这种情况下模型就退化成了BAFAM模型。而当θ=1时，意味着影子吸引力wj=θvj=vj，即竞争企业的产品对产品j的用户的吸引力等于产品j本身的吸引力。这说明从产品j溢出的需求完全转移到竞争对手提供的可替代产品中去，即所有溢出的需求都损失了。这种情况下模型就退化成了IDFAM模型。θ∈（0，1）则表明会有部分的溢出需求转移到竞争对手，而部分的需求转移到本公司提供的其他替代品中，且损失的概率随着θ的增加而增加。这就是本书提出的CFAM模型，它更加符合实际。而θ也可以被看成是市场竞争激烈程度的指示器。θ越大，市场竞争越激烈，溢出的需求损失得越多，挽回得越少。

表6-4记录了CFAM模型的解。“列数”、“行数”分别记录了不同测试案例中的变量数和约束数。“整数变量”指的是模型中的0，1整数变量的个数，它的个数可以由机型类型数和航段数的乘积得到，即k×l。θ的取值如上述，分别取θ=0.0，0.3，0.5，0.7，1.0。“线性解”和“整数解”分别记录了模型的线性松弛解和计算结束时的整数解。“IP-LP的差值”等于（线性解-整数解）/线性解。“Opt差值”指的是最优解差值，它是当前结点的线性最优解和整数最优解的差值。“时间”是整个模型的求解时间。

表6-4　CFAM 模型的性能特征

续表(www.xing528.com)

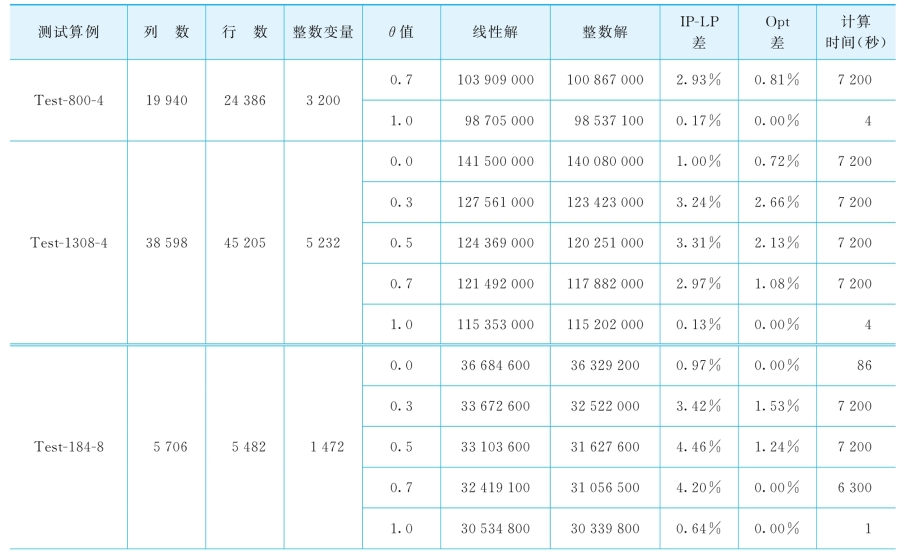
续表

从表6-4可以看出，求解CFAM模型非常耗时，甚至得不到最优解。当设定计算时间为2个小时，在所有的40个大小算例中，有18个算例得到了最优解，平均最优差值为1.0%。计算所耗时间跟跟模型中航段的数量和机型的数量相关，随着数量的增加，耗时呈指数级增长。所有算例中θ=1（对应于IDFAM）的算例都在较短的时间内得到了最优解，这是因为θ=1默认了所有的溢出需求不会被其他替代品重获，所以无须计算溢出需求在不同产品间的转移，这大大节约了运算的时间。

另外，在其他算例的求解过程中，我们注意到第一个整数可行解的产生用时很长。根据定理6.1，IDFAM的最优解是CFAM模型的一个可行解，其值是CFAM的一个下界。为了缩短求解的时间，把IDFAM的解设为CFAM的初始可行解，在此可行解的基础上对CFAM模型继续优化以求得最优解。通过设置初始解，在设定的2小时计算时间内，4个机型的算例中除θ=1之外的其余16个算例中有7个达到了最优解，在8个机型的案例中有3个达到了最优解。另外，值得注意的是，目标值随着θ值的增加而不断减小。因为θ代表着市场竞争的激烈程度，其值越大，预示着会有越多的溢出需求损失，相应的目标收益就会减少。