CFAM的计算结果：详细分析与解读

表6-3记录了有适度竞争情况下（θ=0.5）CFAM的运算情况。主要记录了以下内容：①问题的规模（列数、行数和0-1变量数）；②CFAM的计算结果（线性解、整数解、IP-LP差值、最优值差、运算时间）。

表6-3　CFAM的性能特征（θ=0.5）

续表(www.xing528.com)

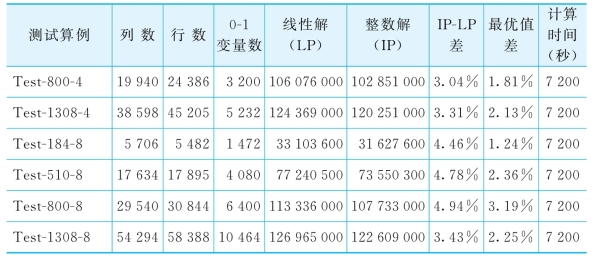
从表6-3可以看出，设定运算时间为2个小时，只有一个最小的算例得到了最优解，其他算例的最优值的差距在1.28%到3.19%，对于航空公司战略规划层面的优化问题，这个差值是可以接受的。同时我们还可以从倒数第三列看到整数解和线性松弛得到的解的平均差值小于4%，这说明我们的模型比较科学。另外，图6-6比较了四个算例在分别有4个机型和8个机型的情况下的利润情况。图6-6表明在8个机型的情况下，利润会比4个机型情况下平均要高4%，且市场规模越小，利润差越明显。这比较容易理解，因为机型越多，模型会根据航段的实际需求选择最经济的机型匹配，以实现利润的最大化；而机型越少，可选择的余地较小，势必会导致成本的上升或者需求的溢出，从而减少了利润。但是我们的模型中并没有考虑因增加机型而造成的运营成本的增加：比如由于机型的增多，相应的维护维修成本、机组成本等的投入增加明显。所以在实际的航空公司运营管理中，可以根据航空公司的规模、运营的线路，在做机型选择时通过平衡收益和成本确定恰当的机型投入类型。

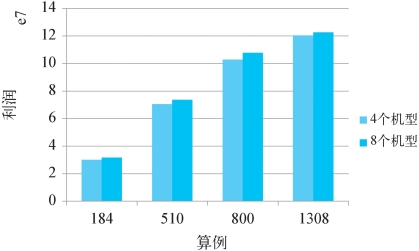
图6-6　四种算例在不同机型数量下的收益比较