机型分配模型优化解析

这一节主要介绍最基本的机型分配模型。机型分配的目的是通过为每一个航班分配最合适的机型从而实现利润的最大化。在基本的机型分配模型中，机型分配问题就是一个多产品网络流问题，如图6-1所示。这是一个两机型两机场的时空网络，横轴表示机场，分别是A、B机场；纵轴表示时间，从早上9∶00到晚上12∶00。机型1的线路用实线表示，机型2的线路用虚线表示，每一种机型包括三种弧，分别是在空中的航班弧、地面弧以及连接机场首尾节点的弧。网络中的节点表示某个机场在一天中某个特定时间航班的进出港情况。

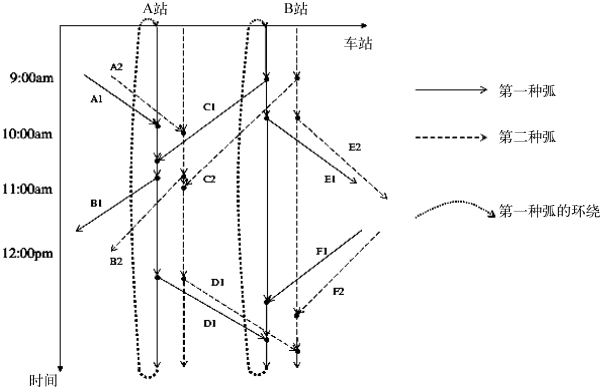
图6-1　机型流的时空网络图

Hane等人（1995）提出了基于时空网络的基础机型分配模型（Basic Fleet Assignment Model，BFAM）[153]。为了方便对BFAM讨论，首先给出以下参数和变量的定义：

集合

A：机场集合，下标用a表示。

L：航班表上所有的航班集合，下标用l表示。

K：不同的机型集合，下标用k表示。

T：所有机场中出发或到达时间的有序集合，下标用t表示。t时刻的事件发生比t+1时刻早。假定|T|=b，那么1是最早的事件发生的时间，而b是最后的事件发生的时刻。

N：时空网络中节点的集合，每一个节点n∈N由k，a和t唯一确定。

L+（kat）：节点nkat的流入航班集合。

L-（kat）：节点nkat的流出航班集合。

参数/数据

Fk：机型k的飞机数。

rkl：当把航班l分配给机型k时的期望收益。

ckl：当把航班l分配给机型k时的运营成本。

决策变量

fkl：二进制变量，如果航班l（l∈L）分配给机型k（k∈K），那么fkl=1，否则fkl=0。

ykat：在机场a∈A，t∈T时刻地面上的机型为k的飞机数量，同时ykat也可以看成是在机场a∈A，t+1∈T时刻前地面上的机型为k的飞机数量。

有了上述对参数和变量的定义，下面给出BFAM模型的表达式：

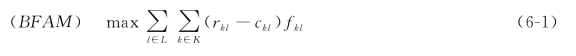
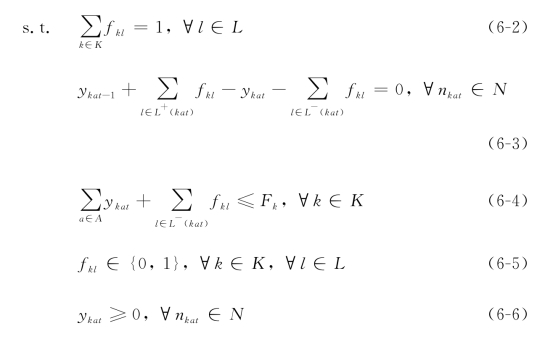
式（6-1）是目标函数，它是使总利润最大化，这里的总利润等于总收益减去总运营成本。式（6-2）是航班覆盖约束，它确保每一个航班只能分配到一个机型。式（6-3）是机型平衡约束，表示的是每一节点飞机机型的流量。式（6-4）是机队规模约束，确保所有被用到的机型数量应该不大于该机型的总数量。式（6-5）—式（6-6）是0-1变量约束和非负变量约束。

但BFAM是一个基于航段的模型，其中的系数rkl是航段的收益，它可以通过多种方式计算求得[166-167]。通常，一个包含多个航段的航程的价格会按一定的分配规则划分到各个航段。目前的分配规则主要包括两种：①航程的价格均等地分到它所包含的所有航段中，每一航段差别地均分航程价格；②航程的价格按不同航段里程长度的比例进行划分，即每航程分得的价格比例等于其在总航程的距离比例。然而，这种类型的收益估计可能很不准确[139]。对于多航段航程，如果某一航段座位全部售出，那么所有用到这一航段的航程将不能出售。而在BFAM模型中，航段可以看成是相对独立的，不受其他航段影响，这显然和实际不符。事实上，任一航段上的存量决策都直接或间接影响了其他航段的需求和存量决策，这一现象被称为网络效应[167-168]。

可以修改BFAM以覆盖网络效应的问题，只需要将模型中的基于航段的收益用基于航程的收益来代表即可。基于航程的模型还会用到以下一些符号。

J：航空公司提供的所有产品集合，下标用j或p来表示，可以是单航段产品也可以是包含多个航段的产品。

SEATSk：机型k的容量。

Dj：对航程产品j的不受限需求量。

rj：航程产品j的价格。(www.xing528.com)

alj：0-1指示参数，如果航程产品j用到航段l，那么alj=1，否则alj=0。

xj：航程产品j的销量。

通过对增加的符号的定义，改善的机型分配模型（Enhanced Fleet Assignment Model，EFAM）如下式所示：

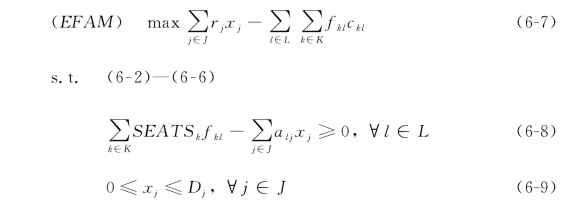
目标函数（6-7）是使总的利润最大化。式（6-2）—式（6-6）和BFAM中的约束意义相同。式（6-8）是容量约束，即保证所有用到该航段的航程销售出去的座位的总数不能大于该航段的座位容量。式（6-9）保证产品j的销售数量应该大于等于0小于等于对该产品的无约束需求。注意xj这里没有规定是整数，因为是在平均需求的基础上建立的上述模型，所以xj可以是分数。

EFAM是一个简单的基于航程的模型，但是从约束条件（6-8）和（6-9）可以看出，模型只满足了座位容量这么多的需求，而未被满足的需求则会溢出，EFAM假设所有溢出的需求都不能被再次挽回。然而，实际上，一部分的溢出需求有可能会被其他可替代的产品重新挽回。为了处理需求的溢出和挽回的问题，Barnhart在2002年[8]提出了一个基于航程的机型分配模型（Itinerary-based Fleet Assignment Model，IFAM）。IFAM模型的表达式我们将在下面给出，这里再定义两个要用到的参数。

：从产品p溢出的需求被产品j挽回的概率，它是被产品j成功挽回的转移需求占p的总溢出需求的比例。

Dl：对航段l的总需求，其中Dl=∑j∈JaljDj。

基于上面的符号，IFAM可以定义为：

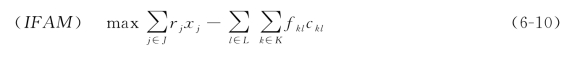
s.t.(6-2)—(6-6)

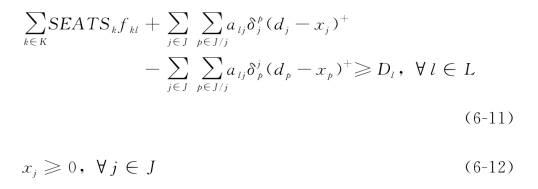
除了约束（6-11）—（6-12）外，IFAM的数学公式同EFAM中的一样，约束（6-11）是容量约束。对航段l来说，表达式是从产品j中溢出的旅客人数，而是被产品j挽回的旅客人数。式（6-12）是保证xj是一个大于0的正数。尽管约束条件（6-11）是非线性的，但是它通过引入其他变量可以很容易转化为线性的。

IFAM假设所有的溢出需求都能被其他替代品（包括不购买）按既定比例全部挽回。在IFAM中，乘客的挽回率可以用市场份额指数（Quantitative Share Index，QSI）来计算。但事实上，如果考虑市场上所有的产品，用QSI来准确计算挽回率的方法很难实现[8]。Barnhart等在其文章中对挽回率的计算及影响因素做了详细的分析，证明用QSI求得的挽回率只是一个粗略的估计。如果不考虑市场竞争，IFAM假定所有的溢出需求会被本公司提供的其他替代品全部挽回，是对市场的过于乐观的估计。而且，在文献[8]的模型中，作者还把IFAM中的挽回率认为是一个常量，不随替代产品的集合变化而变化，这样得到的结果可能并不准确。

Lohatepanont等2002年的文章[169]中考虑了挽回率随市场上在售产品变化的情况，部分解决了挽回率是常量的问题。图6-2为文献[169]中的一个例子。

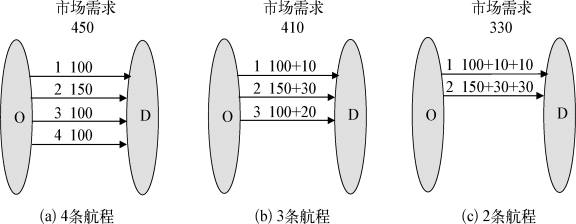
图6-2　供给和需求的相互作用

在这个例子中，假设有4条航程，在图6-2（a）中，除第二个航程有150个需求外，其他的每一个航程都是100个需求。如果删除第4条航程（如图6-2（b）所示），那么原来航程j4的100个需求中的10个会转移到j1，30个会转移到j2，20个会转移到j3，其他40个溢出需求将会不购买任何产品。所以有当航程j3和j4同时删除时，航程j1和j2增加的总需求分别是整个市场的有效需求估计是330。

但是在Lohatepanont等（2004）的文章中[169]，作者认为“330”是对市场需求的过高估计，因为市场占有的份额可能会比规模份额下降更快[170]。市场占有率同规模份额之间的关系可用以下式来表示[171]：

在这个等式中，MSf表示的是航空公司f的市场占有份额，FSg是航空公司g的市场规模份额，m是指市场上相互竞争的航空公司数量，β≥1代表的是市场规模对市场份额的影响，β越大，影响越大。对于大多数航空公司来说，其市场规模份额（FS）一般是小于0.5的，所以其市场占有率的下降会比规模份额的下降明显要快。这种关系如图6-3所示。在市场规模比例小于0.5时，市场占有率的下降要快于规模的下降。

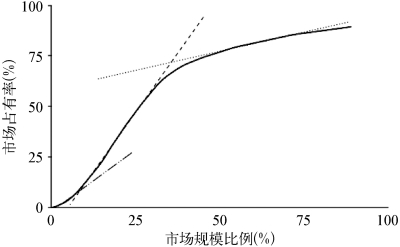
图6-3　市场占有率同市场规模比率之间的S曲线关系

根据上述公式及市场占有率同市场规模比率之间的S曲线关系，当两个航程同时取消时，为了更加准确地计算调整后的需求量，作者用到了二阶度修正项（second-order degree correction term）的概念。同理，作者证明如果有n个航程同时取消时，就要用到n阶度修正项（nth degree correction terms）[169]。但是，这个采用n阶度修正项的方法有两个难点。首先高阶的修正项很难计算；其次，即使采用了n阶修正项，其结果也可能是不准确的。

下面用一个简单的例子（图6-4）加以说明。图6-2和图6-4最大的不同是对溢出和挽回后的需求计算。简单来说，如果不考虑竞争，当航程j3和j4同时取消时，对航程j1来说，其从航程j3挽回的需求通常要比只有航程j3取消时的挽回需求要大。这是因为航程j3从航程j4挽回的一部分需求因为航程j3的取消而被j1挽回。航程j4到航程j1的需求转移有着相同的情形。所以，航程j1总需求的增加量应该是航程j2总需求的增加量为=+70。所以总的市场有效需求应该是350。

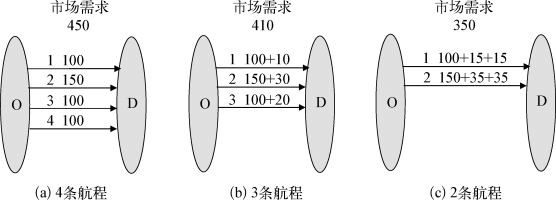
图6-4　供给和需求相互作用的另一种表示

最近，在收益管理领域中已经有人考虑到了这种情形[51]，作者用广义的吸引力模型极好地解决了溢出与挽回的计算。