基于需求转移的客运收益管理：计算结果比较

表5-5比较了基本模型、两阶段启发式算法和遗传算法的解。遗传算法（GA）被广泛地应用于大规模的组合优化问题求解，并且取得了相当大的成功。所以有必要把我们提出的两阶段的启发式算法和遗传算法进行一下比较。表5-5中两阶段启发式算法和遗传算法的差值的计算是和BM相对比得到的，比如两阶段启发式算法下的差值是通过下式计算得到的：。

从表5-5中可以看出，两阶段的启发式算法给出了最好的解。具体来讲，在两阶段启发式算法的18个测试算例中得到了16个算例的最好解（加粗的字体表示是该算例中的最好解）。平均比BM的解增加了1.65%。而剩下的2个测试算例中，BM和两阶段的差值很小，甚至不到0.1%。当测试算例规模较大时，两阶段算法表现要比BM明显要好，即使对小的算例来说，当总需求较低时，两阶段算法也会比BM表现明显要好。遗传算法在所有的测试算例中表现最差。另外，需要指出的是，对44阶段和66阶段的算例来说，两阶段启发式算法的运算时间要远远低于BM和GA。

图5-6对比了算例T-11-66-1.0在整个规划期内每一路段的累积座位数。BM所在的列表示的是在整个规划时间内通过BM模型求得的每个路段的累积分配座位数，可以用以下公式求得：∑t∈T∑j∈Jlxcjt+∑t∈T∑j∈Jl∑c′∈C/{c}yc′cjt。DM这一列代表的是在整个规划时间内通过DM模型求得的累积分配到每一路段的座位数，可以通过下面的式子计算得到：∑t∈Txclt+∑t∈T∑c′∈C/{c}yc′clt。DM→BM所在的列表示的是通过二阶段启发式算法，最后分配给各路段的座位数。(www.xing528.com)

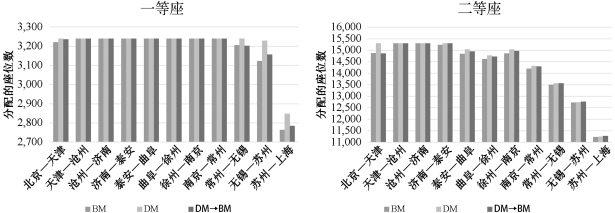
图5-6　不同路段的累积座位分配数

从图5-6可以看出，对大多数路段来讲，这三个列分配了大致相同的座位数量。其余不同的路段中，DM一直是数量最大，而BM是数量最小的列。这三列主要的不同体现在起点附近和终点附近的路段中。这一结论对其他的算例也同样成立。图5-6更加明确地表达了两阶段启发式算法能为每一路段分配更多的座位，所以它求得的解要比BM更好。