基于计划的模型和线性松弛分析简介

从上述的基本模型BM公式中可以看到，如果没有式（5-4）的约束条件的话，BM可以分解成|T|个相互独立的单阶段、多等级的问题。也就是说，众多的单阶段、多等级问题是靠需求的溢出和转移联结起来的。我们提出了一种表示MPMC-RPRM问题的新模型，在这个新模型中，每一个变量代表的是一个单阶段、多等级铁路客运收益管理（Single Period Multi Class Rail Passenger Revenue Management，SPMC-RPRM）问题的完整解，它们通过相邻阶段间的需求平衡约束链接起来。目的是通过选择每一个单阶段的解使利润达到最大。

令Pt表示在时刻t所有SPMC-RMRP问题可能解的集合。为了便于说明，下文中用术语“计划（plan）”来表示单个阶段的解。每一个计划p∈Pt中包含了以下详细信息：累积需求zcjt、分配给本等级原始需求和其他等级转移需求的座位数量xcjt、本阶段溢出到下一阶段的溢出需求δcjt。但是和BM不同的是，在BM中这些值是要求解的决策变量，在基于计划的模型（PBM）中，这些值对任一给定的计划p来说却是常量。为了使后面的讨论方便，我们对每一个计划p∈Pt中的一些符号做如下定义：

符号

up：0-1参数，如果计划p中的车次已经确定则有up=1，否则up=0。

xcjp：非负的整数参数，分配给计划p中旅程j的c等座座位数。

yc′cjp：非负的整数参数，计划p中旅程j的c′等座需求溢出到c等座的需求数。

zcjp：计划p中对旅程j的c等座的累加需求。

δcjp：整数变量，计划p中旅程j的c等座的溢出需求。

θp：0-1变量，如果计划p被选中则有θp=1，否则θp=0。(www.xing528.com)

那么计划p的利润可通过下式计算求得

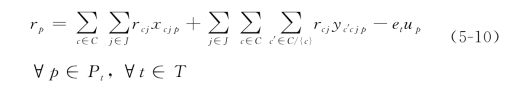
基于计划的模型其数学公式可表示为

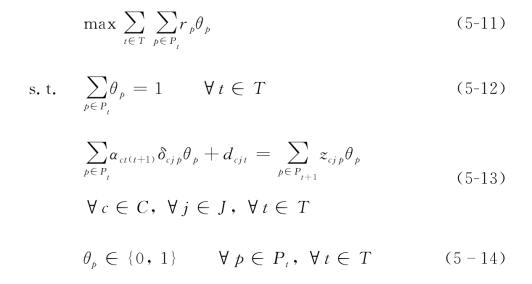
其中目标函数（5-11）是使总的利润最大化。式（5-12）中的约束条件确保每一个阶段t都有且仅有一个计划被选中。式（5-13）是溢出需求的约束，它表明累积需求主要来自两个方面，即前一阶段的溢出需求和当前阶段的原始需求。在这个模型中，共有O（|C||S|2|T|）约束条件，比BM中的约束条件少了很多，但是PBM中的计划变量却非常庞大。实际上，基于计划的需求模型PBM是BM的一个Dantzig-Wolfe分解。对于变量庞大的模型来讲，利用Dantzig-Wolfe分解一般都能为原整数规划问题找到较好的线性规划松弛，得到近似最优解。但是在问题中，这个线性松弛模型PBM却并不理想。

例　假设一个仅包含单个座位等级、单个旅程和单个阶段的问题。需求d=70，火车座位数n=100，车票价格r=10，固定运营成本e=800。有三种可能的计划p1、p2和p3，如表5-2所示。

表5-2　最优线性规划松弛和最优整数规划解的对比

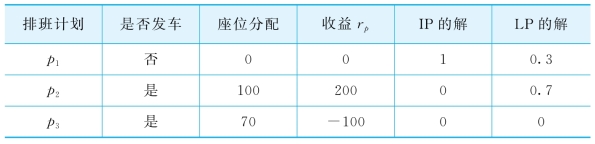
因为总收益小于固定成本，最优的整数规划解应该是θp1=1且总收益为0。但是，线性规划松弛的最优解却是θp2=0.7，θp1=0.3，总收益为140。这是因为线性规划松弛的收益受需求数量d的影响非常大。当时，线性规划松弛的最优解和整数规划的最优解的差等于且IP-LP的差值永远为1。所以当d稍小于时，PBM的线性规划松弛为最优整数规划解所提供的信息很少（甚至可能是误导）。同样，BM也面临着这样的问题。