MPMC-RPRM问题的基本模型：需求平衡与利润最大化

为了方便后面的讨论，先定义一些变量：

变量

ut：0-1变量，如果车次t在结果中被选中ut=1，否则ut=0。

xcjt：整数变量，分配给对车次t中旅程j的c等座需求的c等座位数。

vc′cjt：0-1变量，如果c等座的座位分配给了车次t中旅程j的c′等座的溢出需求，则vc′cjt=1；否则vc′cjt=0。

yc′cjt：整数变量，分配给车次t中旅程j的c′等座的溢出需求的c等座位数。

zcjt：对车次t中旅程j的c等座的累加需求。如果前一时段t-1没有溢出需求，则zcjt=dcjt；否则zcjt＞dcjt。

δcjt：整数变量，车次t中旅程j的c等座在t时段的溢出需求。

给定上述变量的定义，MPMC-RPRM问题的基本模型（BM）可表示如下：(www.xing528.com)

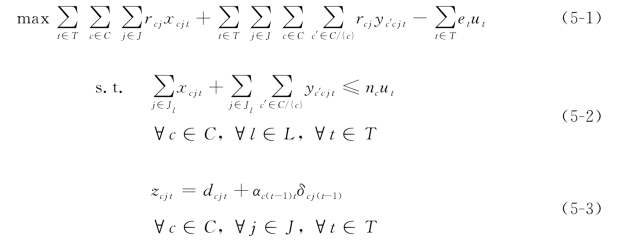
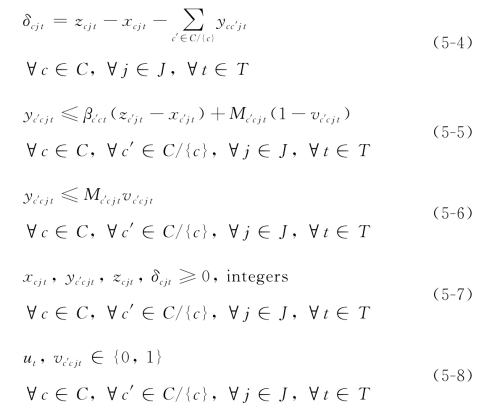
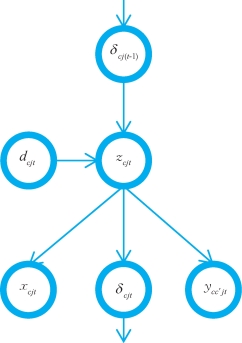
图5-4　不同变量间的需求平衡图

目标函数（5-1）是使总的利润最大，总利润等于总的售票收益减去总的运营成本。式（5-2）的约束条件是确保任一路段l的c等级座位的售出数应小于等于c等级的总座位容量。式（5-3）的约束条件是指对时刻t旅程j的c等级的累积需求包括两部分：一部分是t时刻的原始需求，另一部分是来自前一阶段t-1的溢出需求。式（5-4）的约束条件是用来计算c等级的溢出需求。结合对变量δcjt的非负约束，还要确保时刻t旅程j的c等级的座位数应小于等于t时刻的累积需求zcjt。当t=0时，为了避免与边界条件的混淆，假定δcjt=0。式（5-3）—式（5-4）可以视为需求的平衡约束，可以用图5-4来描述。

对每一个累积需求节点zcjt，有两个输入流：dcjt和αc（t-1）tδcj（t-1），即原始需求和上一时段到这一时段的转移需求。同样地，每个zcjt节点还有三个输出流：分别是xcjt、yc′cjt和δcjt，即被满足的需求、转移到其他等级的溢出需求和到其他时段的溢出需求。式（5-6）—式（5-8）是计算从其他等级转移到c等级的需求数，即yc′cjt=βc′ctmax{zc′cjt-xc′jt，0}。如果vc′cjt=0，yc′cjt也应等于0；否则yc′cjt=βc′ct（zc′jt-xc′jt）。Mc′cjt的最小值可以通过下式计算得到。

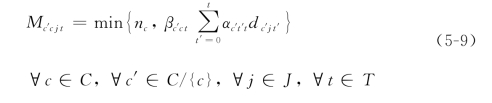
其中，αc′t′t是对c′等级的座位而言，从t′时刻到t时刻的需求转移率，是计算了从0时刻到t时刻对旅程j的总累积需求。所以Mc′cjt是t时刻旅程j能从c′等座到c等座的最大可能的转移需求。式（5-7）—式（5-8）是对变量的整数约束和0-1约束。

因为BM模型中有大量的0-1整数变量和大M约束，所以在解决大规模的算例时，很难求得它的最优解。求解时，放松了对变量（x，y，z，δ）的整数约束，把这个放松了整数约束的松弛模型称为R（BM）。R（BM）模型的空间复杂度非常大，约有O（|C|2|S|2|T|）个0-1变量和O（|C|2|S|2|T|）个约束条件。