根据4.3节的模型，通过编写matlab程序可计算出停止销售低价票的最佳停止点。如图4-5所示，假定航班B是违约者，在某一点首先停止销售低价票，航班A检查自己的剩余座位数，根据对需求的预测确定自己的最佳对策。例如航班B在第60阶段剩余座位为4时停止销售低价票，航班A如果剩余座位数小于或等于2，则在下一阶段也关闭低价票，否则继续开放直到剩余座位为2再关闭。
图4-5中上面两条线是考虑需求双向转移的最佳停止线，比下面两条只考虑需求水平转移的停止线高。说明考虑需求双向转移时保留给高价票的座位数较高。
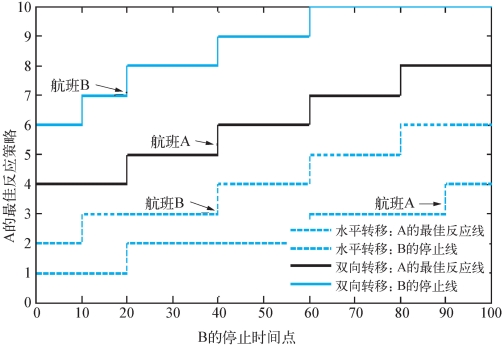
图4-5 最佳停止线
表4-2 最佳停止点与β的关系(www.xing528.com)
表4-2揭示了最佳停止点与各变量间的关系。首先令选择系数β从0逐渐增加到1，β的值越大意味着在价格相等时有更多的旅客会选择航班A，所以航班A的最佳停止点处的剩余座位数y
（n）是随β非减的，而航班B的y
（n）随β非增。除价格因素外，如果旅客更偏好于某公司，则该公司应为高价票保留更多的座位。
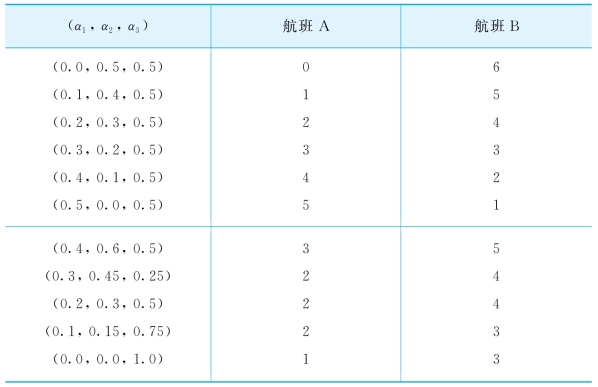
保持弹性旅客的比例和偏好系数不变，即α3=0.5，β=0.4，改变类型1和类型2的旅客比例。表4-3右上方结果表明停止点是航空公司忠诚顾客比例的增函数。在表4-3的右下方，改变α3的值，保持β=0.4，类型1和类型2的旅客比例α1∶α2=2∶3。由结果可知，弹性旅客的比例越高，即价格敏感的休闲旅客越多，最佳停止点保留给高价票的座位数越少。航班A的最佳停止点座位数随着α1（忠诚顾客的比例）和β（弹性顾客购买航班A的比例）的增加而递增，但是，随α1的改变幅度要比随β改变幅度大。所以，航空公司应当设法通过非价格手段来增加忠诚顾客的比例，通过灵活定价吸引更多的弹性顾客。
表4-3 最佳停止点与（α1，α2，α3）的关系
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
