个子航空公司纳什均衡决策,最优控制策略

时间：2023-05-22 理论教育版权反馈

【摘要】：两个博弈方知道并严格遵守这一约定，保证了报复机制的可信性。采取绝不宽恕的触发策略，且制定的报复机制是可信的。□定理4.2考虑需求双向转移下停止点剩余机票数比仅考虑水平转移下的机票数要多。证明目前的文献仅考虑了需求在相同产品间的水平转移，忽略了不同航班的不同等级间的纵向和斜向转移。这意味着低价票开放时，考虑需求双向转移对低价票的需求率更高。

个子航空公司纳什均衡决策,最优控制策略

两个航空公司座位分配决策模型是个双人有限次重复博弈，在每一回合的博弈中，博弈方都有两种策略选择：开放低价票和关闭低价票。原博弈的收益矩阵如图4-3所示，数组中第一个数为航班B的收益，第二个数为航班A的收益，它是一个完全信息的静态博弈，双方同时选择对策。

pagenumber_ebook=80,pagenumber_book=64

图4-3　原博弈的收益矩阵

原博弈中，如果一方选择关闭低价票，而另一方选择开放低价票，则依据前面的假设，所有类型3的旅客会流向开放低价票的航班，因此，另一方也会选择开放低价票，所以，（开放，开放）是原博弈的一个纯策略纳什均衡。然而当只有少数机票剩余且需求充足时，理性的决策者都会选择关闭低价票以获得更大的收益，所以，（关闭，关闭）也是一个纳什均衡。我们还假定低价票一旦关闭将不再开放，所以，（开放，关闭）和（关闭，开放）也会是另外的两个纳什均衡。原博弈是一个有多个动态纳什均衡的博弈模型。

重复博弈是原博弈在每一个销售时间段的重复进行，共进行N个回合的博弈。重复博弈的收益矩阵如图4-4所示，与图4-3相似，不同之处在于在重复博弈中，其收益是由式（4-7）、式（4-8）、式（4-13）、式（4-14）计算求得，是从当前销售阶段到飞机起飞这一时间段的最大期望收益之和（不考虑贴现）。

pagenumber_ebook=81,pagenumber_book=65

图4-4　重复博弈的收益矩阵

假设两个博弈方都是理性的，依据当前剩余座位和对将来需求的预测，决定是否关闭低价票以实现自身收益的最大化。两博弈方首先采取试探合作的策略，开始时双方都采取（开放，开放）的策略组合，一旦发现对方不合作则也用不合作相报复的策略，即触发策略。

航班A：开始时选择开放，如上一阶段博弈的结果是（开放，开放），则在本阶段决策是否依然选择开放，且一旦选择关闭，则启动触发策略，即到销售期结束一直保持关闭。如果上一阶段博弈的结果是（开放，关闭），即B如果在上一阶段选择了关闭低价票，那么触发策略对B生效，B只能保持关闭直到销售结束，而A可以比较关闭和开放低价票时的收益，当且仅当GA（n，yA）＞FA（n，yA）时，选择关闭，否则选择开放。

航班B：其策略同航班A。

这个重复博弈模型中用到了触发策略，即一旦有博弈方背叛了原来的合作策略，守约方将在下一轮采取策略进行报复。在上面的重复博弈模型中，“低价票一旦关闭将不允许再次开放”就是对违约者的惩罚，即守约方可以根据自身收益情况选择开放或关闭的策略，而违约方只能保持关闭直到博弈结束。两个博弈方知道并严格遵守这一约定，保证了报复机制的可信性。

我们用逆推归纳法来分析这个重复博弈，先分析最后一个阶段，依次向前逆推。博弈方了解整个博弈过程，本轮决策前各航班所剩机票数为（yA，yB），假设在上一回合的决策中低价票依然开放（如果上一轮低价票已经关闭，则本轮依然关闭），航空公司需要决策的问题是在本轮是否继续开放低价票。选择关闭低价票的充分必要条件是：GB（n，yB）＞FB（n，yB）或GA（n，yA）＞FA（n，yA），最佳停止点y*（n）可由下式得到：

pagenumber_ebook=82,pagenumber_book=66

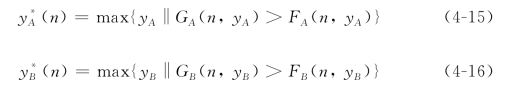
定理4.1　博弈方的上述触发策略组合是该重复博弈的一个子博弈完美纳什均衡。(www.xing528.com)

证明　由前面的分析可知，每一个阶段的原博弈是有多个纯策略纳什均衡。采取绝不宽恕的触发策略，且制定的报复机制是可信的。假设某次合作中，航班B首先违约，在当期关闭低价票，航班A只有在本期合作结束后才能观测到航班B的选择，所以航班A的当期选择是开放，在接下来的所有策略中，选择有利于自己的策略，而航班B只能保持关闭直到结束。

各博弈方的最佳停止点满足式（4-15）和式（4-16），该重复博弈的均衡路径如下：

●max（n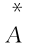 pagenumber_ebook=83,pagenumber_book=67 ，n）≤n≤N，选择策略组合（开放，开放）。