本章讨论的问题是竞争环境下单航段的多个航班的动态舱位分配策略。每个航班提供多个价格等级,旅客依据自身偏好选择不同产品,但当旅客的初始需求不能得到满足时,其需求会在不同产品间自由转移。包括在不同航空公司相同等级间的溢出转移即水平转移,同一航班间不同等级间的纵向转移,不同航班、不同等级间的斜向转移。在这种市场环境下,航空公司制定座位分配策略时,要综合考虑竞争对手的策略。为了简化问题,这里只考虑两个竞争航班的情况(图4-1)。假设两个航班的起飞时间非常接近,即销售期可近似相等,等分为N个阶段,其中,N是开始售票时间点,0是销售结束时间点,即飞机起飞时间。各自的容量分别为C1和C2(C1可以等于C2),不考虑取消和超售的情况。假设两航班都提供两种不同的价格等级r1和r2,且r1>r2。假设相同价格等级的机票是同质的,不同价格等级的机票是异质的,不考虑旅客在机型、机上服务等其他因素感知效用上的差异。假设潜在旅客购买机票的一个基本前提是其心理价位高于机票的实际价格,否则会放弃购买。旅客的心理价位(记为v)是独立同分布的,其累积分布函数为F(v),不失一般性,该函数连续可微且严格递增。

图4-1 竞争环境下两航班两等级的需求转移
为了建模的需要,做如下假设:
假设1 所有旅客划分为三类,类型1、类型2和类型3。其中类型1和类型2分别为航班A、航班B的忠实旅客,只购买航空公司A或航空公司B的航班。类型3是弹性旅客。
类型1和类型2的旅客只会购买认定航空公司的航班,即使另一航班提供的机票价格更低,他们也不会改变自己的选择。比如因公出差的商务旅客、航空公司VIP旅客等,他们为了获得积分或里程奖励,往往会选择指定航空公司的航班。类型3这类旅客对价格高度敏感,他们只选择价格最低航班。休闲旅客大多都属于这种类型。基于上述分类和假设,图4-1中所示复杂的多向需求转移可简化为图4-2中所示的水平转移和纵向转移的双向转移情况。
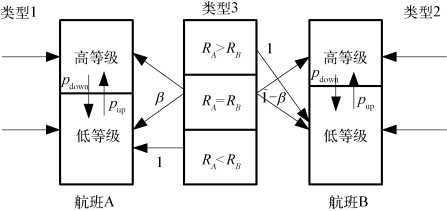
图4-2 三类旅客的需求转移(https://www.xing528.com)
假设上述三类旅客的比重分别为αk(0<αk<1),k=1,2,3且∑αk=1,旅客到达服从齐次泊松分布,总到达率为λ,则每类旅客的到达率为λk=αkλ(k=1,2,3)。
航空公司遵循嵌套的价格机制,在销售期开始时同时开放高低价票。RA和RB分别表示航空公司A和航空公司B的当前可售机票中的低价,当旅客需求到达且其心理价位v≥RA(或v≥RB)时,机票售出的概率为
Pr(v≥RA)=1-F(RA) 或 Pr(v≥RB)=1-F(RB)
假设2 如果低价票开放,即RA=RB=r2,类型1和类型2的低价票需求(r2≤v≤r1)和类型3(v≥r2)的旅客购买低价票,类型1和类型2的高价票需求(v≥r1)会以相同的概率p12降级购买;如果低价票关闭,即RA=RB=r1,所有的高价票需求购买高价票,低价票需求会以相同的概率p21升级购买。
假设3 类型3的旅客购买机票服从以下规律:
●RA≠RB,且v≥(RA∧RB)((RA∧RB)=min(RA,RB))时,选择购买票价更低的航班;
●RA=RB,且v≥(RA=RB)时以概率β购买航班A,以概率1-β购买航班B。
假设4 低价票一旦关闭,在接下来的销售时期内不再开放。这一假设非常重要,它可以避免由策略性顾客的选择行为造成的收益下降,而且被行业广泛接受。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




