嵌套保护水平的重要性

为了探讨期望总收益与决策变量yi的关系，对式（3-6）求关于yi的偏导：

式（3-7）随着yi的增加而减小，是yi的减函数。表达式（3-4）是yi的凹函数，且在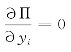时取得最大值。存在一个最优保护水平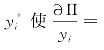0，当且仅当yi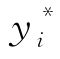＞时，继续接受更低等级的订票需求，否则拒绝，保留给等级i。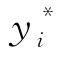满足以下条件：

即

因为Dk服从均值为μk标准差为σk的正态分布，所以，表达式服从均值为hkjpkj））×μk、标准差为的正态分布，所以有

为简化起见，令

则保护水平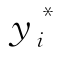可由下式得到

定理3.1　保护水平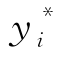是降级转移概率pij（i＜j）的单调减函数，是升级购买概率p（i+1）i的单调递增凹函数。

证明　首先来证明保护水平同降级转移概率之间的关系。

仅考虑i及其以上等级到i+1等级的降级购买概率和保护水平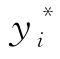之间的关系，所以到其他等级的降级购买概率可看为常数。

对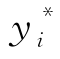求关于pij（i＜j）的偏导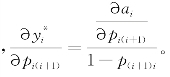因为1-p（i+1）i≥0，所以此处仅考虑分子部分。

其中，

因为对于任一等级来说，hkjpkj＜1，所以

令(www.xing528.com)

由上述假设可知，g是一个量，所以该项的增减性同f（pkj）的增减性。对f（pkj）求导，则有

由此可以得到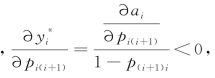所以，保护水平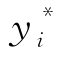是i以上等级的降级购买概率的单调减函数。

同理，证明保护水平同升级转移概率的关系。

因为假定升级转移只发生在相邻的两等级间，所以对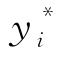求关于升级购买概率p（i+1）i的偏导：

为方便讨论，令

令

首先，证明f（p（i+1）i）＞0。

因为ai是p（i+1）i的增函数，所以有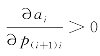。0＜P（i+1）i＜1，所以。

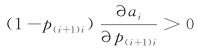根据式（3-10），把ai代入到f（p（i+1）i）中，有下式成立：

根据前面的介绍，yi+1-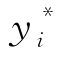=bi+1是第i+1等级的预订限制，且对折扣票的需求往往大于为折扣票分配的预订限制，所以综上，我们证明了f（p（i+1）i）＞0，且是p（i+1）i的增函数。

显然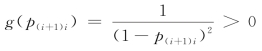，且是p（i+1）i的增函数。所以f（p（i+1）i）×g（p（i+1）i）＞0，即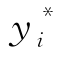是p（i+1）i的单调递增凹函数。　□

定理3.1　说明保护水平随降级购买概率的增加而减小。在实际应用中，要求航空公司应当为不同等级票设置相应的价格栅栏，防止较高等级需求向较低等级需求的转移。同时，定理3.1还说明保护水平是升级购买概率的单调递增凹函数，随着升级购买概率的增加而增加。航空公司为使收益最大化，要尽量提升升级购买的转移概率。降级转移概率和升级转移概率的计算在下面详细给出。