模型用到的参数和变量说明如下:
变量
yi:整数变量,嵌套机制下的各等级保护水平。
bi:整数变量,嵌套机制下的各等级的预订限制,其中,bi=C-yi-1。
参数
C:航班容量。
Di:各等级的原始需求,服从均值为μi方差σi的正态分布。
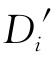 :需求双向转移后的各等级需求。
:需求双向转移后的各等级需求。
pij:如果i<j,pij为降级购买的概率,其中,i=1,2,…,n-1,j=2,3,…,n;如果i>j,pij为升级购买的概率,其中,i=2,3,…,n,j=1,2,…,n-1。
hij(i<j):i等级顾客在销售时段j到达的概率,其中,i=1,2,…,n-1,j=2,3,…,n。
ri:i等级机票价格。
b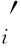 :非嵌套的预订限制,b
:非嵌套的预订限制,b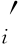 =yi-yi-1。
=yi-yi-1。
需求和容量都是离散的,但通常为了方便建模和简化分析,当需求和容量很大时,也可以把它们看成是连续的变量。当低等级j的需求未被满足时,这些未被满足的低等级需求有可能会放弃购买,也有一部分乘客会提高自己的支付愿望升级购买。理论上,升级购买的需求可以购买任意较高等级i(1≤i≤j-1)的机票(图3-1),但在实际操作中,低等级的需求往往都是价格敏感的,如果等级j关闭,未被满足的需求会考虑当前开放的最低价机票,即升级到相邻的高等级j-1。实际的销售流程如图3-2所示。
根据图3-2所示的转移规律,双向转移后的实际需求D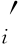 可用下式计算求得:(https://www.xing528.com)
可用下式计算求得:(https://www.xing528.com)
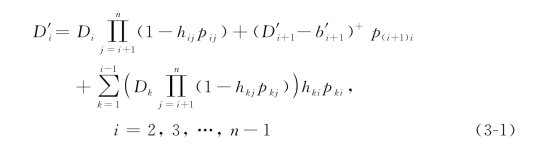
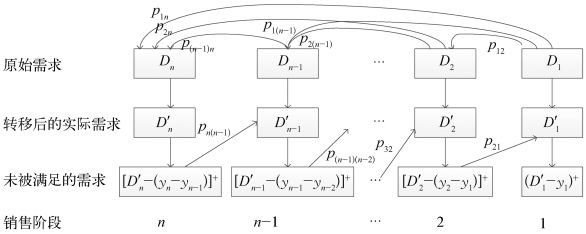
图3-2 实际的升级转移情况
i=1时,最高等级的需求D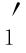 没有从更高等级降级来的需求,i=n时,最低等级的实际需求D
没有从更高等级降级来的需求,i=n时,最低等级的实际需求D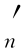 没有从更低等级升级而来的需求,所以,D
没有从更低等级升级而来的需求,所以,D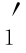 和D
和D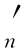 是式(3-1)的特殊情况,可用式(3-2)和式(3-3)分别表示:
是式(3-1)的特殊情况,可用式(3-2)和式(3-3)分别表示:
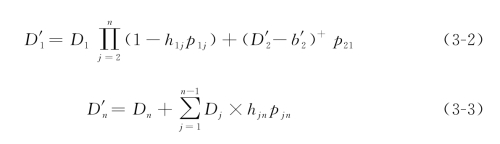
目标函数是使航空公司的收益Π最大化,它是各等级保护水平yi的函数。我们令如下表达式成立,(D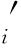 ∧b
∧b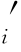 )≡min(D
)≡min(D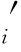 ,b
,b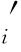 )。则收益函数可表示为
)。则收益函数可表示为
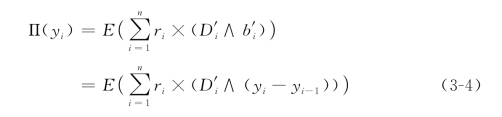
假设在第i个阶段开始时还剩余yi个座位,此时接到一个i+1等级的请求,我们是否要接受该请求,换句话说,我们要为第i及以上等级预留多少座位(即第i等级的保护水平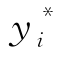 )。要确定保护水平,必须知道将来还会有多少需求。令Si表示i及以上等级的总需求,则有
)。要确定保护水平,必须知道将来还会有多少需求。令Si表示i及以上等级的总需求,则有
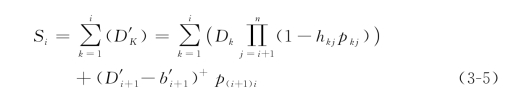
通常情况下,假设对折扣票的需求大于实际开放数,即(D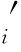 ∧b
∧b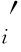 )≡b
)≡b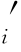 =yi-yi-1,式(3-4)可进一步转化为
=yi-yi-1,式(3-4)可进一步转化为
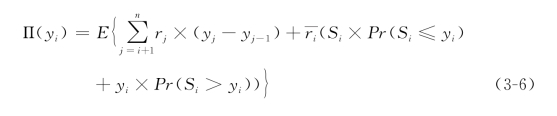
其中,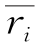 是等级1到等级i收益的加权平均值:
是等级1到等级i收益的加权平均值:
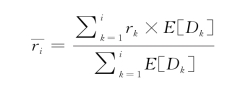
其计算方法可参见文献[126]。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




