基于需求转移的收益管理在竞争环境下的优化

最早对竞争环境下的收益管理展开研究的是Belobaba和Wilson（1997）[52]。他们利用仿真的方法来证明在竞争的环境下，航空公司使用收益管理系统能否提高利润。据我们所知，Li和Oum（1998）[53]是第一个将竞争引入一个两等级的舱位分配问题中，并给出了理论模型，他们重点讨论的是决策变量取整数值且有对称的机票价格和随机需求的竞争情况，但没有考虑成本。后来，研究竞争市场的收益管理文献主要是运用博弈论的理论来研究双寡头竞争环境下的座位分配问题，即由两家航空公司提供两个等级的单航段的竞争问题[54，55]。他们均证明了所研究问题中纯策略纳什均衡的存在性、唯一性和稳定性，而且他们的结论都表明在竞争环境下的低等级的预订限制要比垄断环境下的要少。Netessine和Shumsky（2005）[56]研究了两家航空公司分别销售两个等级机票的竞争问题，需求可以从一家航空公司的某一等级水平溢出到另一航空公司的同一等级（图2-1）。他们假设不同航空公司的每一等级是独立的随机需求，所以，相应的需求结构中共有四个外生的随机需求。模型如下：

航空公司i的低等级需求为：。

航空公司i高等级的可用座位数：。

航空公司i的高等级需求为：。

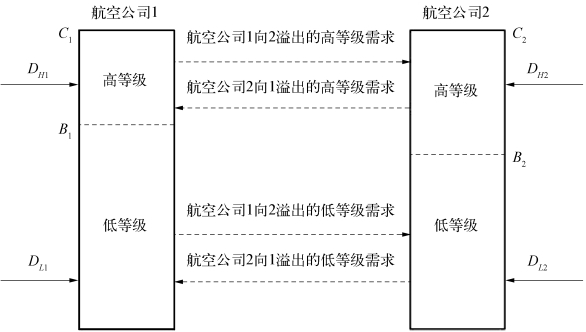
图2-1　水平竞争下的需求转移(www.xing528.com)

航空公司i的总收益为：πi=E[pLimin（DLi，Bi）+pHimin（DHi，Ri）]。

如果给定一家航空公司的预订限制，可以通过求偏导的方法求得另一家航空公司的预订限制。他们证明了在水平竞争情况下，如果四个随机需求联合概率密度函数有多元全正二序（MTP2）性质，则纯策略纳什均衡存在。他们还表明垄断环境下的全价票的预订限制不会小于两航空公司竞争情况下的全价票的总预订水平。但他们的研究都是事先确定预订限制，即构建的是静态模型，不能根据观察到的需求情况进行实时调整，多数情况下，并不能达到收益的最优。

Brumelle，S.等（2003）[57]指出，动态规划可以有效解决竞争环境下的座位分配问题，但因为动态模型求解复杂，鲜有文献研究竞争环境下的座位分配问题。但Yang等（2013）[58]、Liu等（2008）[44]、Lin等（2009）[59]、Hu等（2013）[60]和Gallego等（2014）[61]都从动态定价的角度分析了竞争市场环境下的收益管理问题。Zhao和Atkins（2003）[62]对两家航空公司在同一需求等级上竞争乘客的情况进行了分析，他们给出了联合动态定价和座位分配问题的模型。因为动态非合作非零和博弈模型计算复杂[42]，很难得到它的精确均衡解[63]。为了避免计算的复杂性，Schütz等（2012）[64]和Zhang等（2006）[65]用近似模型求得次优解，但这些近似均衡的结果并不令人满意。

国内的学者对国外研究的成果进行了扩展，陈慧等（2008）[66]将Netessine等（2005）[56]的水平竞争模型由两个价格等级扩充到三等级，并得到了一些有益的结论。汪瑜等（2009）[67]构建了竞争环境下航班舱位控制博弈模型，计算求出各航班低价票的最优预订水平。另外，罗利等分别于2007年[68]和2012年[69]研究了竞争环境下的航班动态定价问题，求出了最优价格切换的时间阈值。

以上是对收益管理理论研究情况的综述，接下来本书从应用的角度介绍一下收益管理在不同行业中的应用研究。