测量房地产泡沫溢出的方法

1.空间相关性检验

检验变量在区域间是否具有空间相关性，通常采用Moran's I指数，数学表达式为：

n为观察的省域个数，xi为观察的第i个省域。wij为空间权重矩阵，近年来不同学者为研究空间问题，给空间权重赋予了不同定义，下文笔者将着重论述。Moran's I指数的取值范围为（-1，1），数值越接近1表明区域间的正向空间相关性越高，数值越接近-1表明区域间的负向空间相关性越高，数值接近0表明区域间不存在空间相关性。表1-6给出了2006—2016年中国各省域房地产泡沫的Moran's I指数检验结果。检验结果显示，2006—2016年各省域房地产泡沫的Moran's I指数都为正值且通过了1%水平下的显著性检验，这说明中国各省域间的房地产泡沫具有非常显著的正向空间相关性。一个地区的房地产泡沫的膨胀会有效带动周边泡沫值的增长，从而产生房地产泡沫的空间溢出性特征。因此，本章拟采用空间溢出效应计量模型衡量一个地区房地产泡沫膨胀对周边地区的溢出程度。空间相关计量模型存在两种：一种为空间滞后模型；另一种为空间误差模型。下文将对两种空间模型进行回归检验，选择最优模型对房价空间溢出效应进行回归。

表1-6　2006—2016年中国各省域房地产泡沫的Moran's I指数检验结果

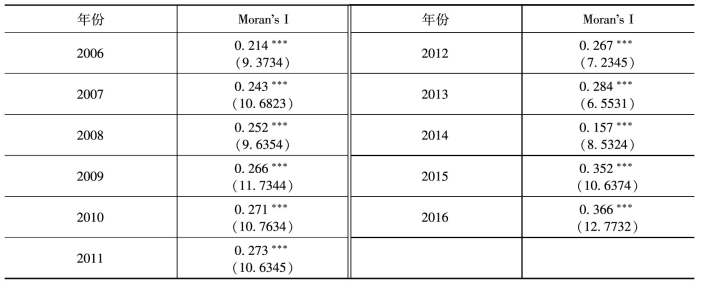
注：***、**、*分别表示通过1%、5%、10%水平下的显著性检验。

2.计量模型

空间溢出的计量通常采用空间相关性来衡量各地区之间，在不同因素影响下是否具有相互影响。空间相关性具体是指在不同区域间的观测样本中，位于i区域的观测值与位于j区域的观测值具有相关关系，用函数表示为Yi=f（Yj），i=1，2，…，n；i≠j。如果回归模型中存在空间相关性，则最小二乘估计是有偏的，估计结果也不具有一致性（LeSage，1999），在这种情况下通常采用极大似然法估计（MLE）或两阶最小二乘法对回归变量进行估计。在分析空间问题时经常会涉及两个模型：空间滞后模型与空间误差模型。

本章根据表1-7检验结果空间滞后模型的显著程度明显优于空间误差模型，后文给出详细分析。笔者着重对空间滞后模型（SLM）进行介绍与探讨。空间滞后模型（SLM）是对某地区变量是否对周边地区变量具有扩散现象（外溢效应）进行分析的计量模型。SLM表达式为Y=pωY+βX+ε，其中Y为因变量；X为n×k阶的外生解释变量矩阵；ρ为空间回归系数；ω为n×n阶的空间加权矩阵，ωY为空间滞后因变量；ε为随机误差项。根据前文的理论研究，房地产泡沫受到货币政策、预期、非住房消费、住房供给与贷款基准利率等因素的影响，基于此构建房地产泡沫的空间滞后模型如下：

lnPop=α0+α1lnPre+α2lnCon+α3lnLoa+α4lnSup+α5lnDen+α6Int+pωlnPop+μ

其中，lnPop是i省市t年的房地产泡沫指标，lnPre是i省市t年的房地产价格增值预期指标，lnLoa是i省市t年的房地产市场资金供给指标，lnCon是i省市t年的非住房消费指标；Int为房地产价格的利率因素；lnDen为各省域人口密度；ωlnPop是空间滞后项。其中ω是空间滞后权重矩阵，表达形式为空间权重矩阵或空间相邻矩阵，该权重矩阵为方块对角阵，每个方块代表的是任意一年的不同省域间的权重矩阵，表示为：

(www.xing528.com)

本章数据为2006—2016年共包括11个年份，因此矩阵中包含了11个W值，而每年又包括30个省域样本，因此ω为330×330的矩阵。接下来将对各省域数据分别进行未考虑空间效应的OLS估计、考虑空间效应的空间滞后模型估计与空间误差模型估计，根据检验结果选择最优模型。

在选择模型过程中，笔者先选取最简单的“0—1空间权重矩阵”进行模拟。即假设地理位置接近的省域赋予W值为1，认为只有地理上接近的省域间才会有房地产价格的空间溢出效应，否则为0。即Wi，j=1或0（i与j邻近为1，不邻近为0）。得到空间效应模型回归数据表1-7。从回归结果可以看出，OLS模型拟合优度为0.9673，模型整体通过了5%的显著性检验。由于Moran's I统计值显示OLS回归误差的空间相关性较明显，需要加入在模型中引入空间效应，笔者引入空间滞后模型与空间误差模型。

表1-7　空间效应模型回归数据

表1-7中显示了对两种空间模型的回归结果，拉格朗日乘数滞后项（LMLAG）与稳健滞后项（R-LMLAG）都通过了1%的显著性水平，且LMLAG较拉格朗日误差项（LMERR）在统计值上更加显著，R-LMLAG较稳健误差项（R-LMERR）更加显著，从5个统计量可以看出，SLM比SEM的拟合优度更高。将OLS估计结果与SLM估计结果相比发现，SLM的拟合优度在OLS基础上有所提高达到0.9785。对数的似然函数值从未考虑空间效应模型中的101.042，提高到SLM模型中的184.452。从表1-7的计量结果可以看出考虑到空间效应的SLM模型更加适合用来拟合房地产泡沫的空间溢出效应。初步估计结果显示，房地产泡沫在区域间具有正向溢出效应，且对房地产泡沫值增长的影响贡献率达到0.975。但此估计结果只考虑了0—1空间权重，在实际中房地产泡沫的区域溢出效应不仅存在于相邻的地区之间，还存在于周边地区乃至经济相关地区。因此，笔者将地理权重矩阵与经济—地理权重矩阵引入，在下文进一步研究不同空间权重矩阵对房地产泡沫空间溢出效应的影响。

3.空间权重设定

本章探讨的空间权重矩阵是赋予周边不同省域房地产泡沫影响力的不同权重，用来衡量泡沫的空间溢出效应。一般空间权重矩阵的构建共包括以下三种方法（Anselin& Bera，1998；康继军，2009；魏下海，2010；于斌斌，2015等）。

（1）0—1权重矩阵，认为地理上相邻的地区间才会产生空间溢出性，赋予W值为1，否则为0。这种方法直观且操作简单，在计量空间问题时得到广泛应用。但是采用这种方法容易遗漏空间溢出的部分信息，即使不相邻的区域间也会产生空间溢出性，且地理较接近发展模式相似的省域间也会产生空间溢出效应。因此，在讨论房地产泡沫空间溢出性中我们需要将地理权重矩阵与经济权重矩阵引入进行比较，从而得到最优选择。

（2）地理权重矩阵，即将含有距离因素的空间单元引入权重矩阵，认为不相邻的省域间也存在空间联系，对角线上的空间权重都为0，Wi，j是矩阵第i行和第j列的元素，表示第i个地区与第j个地区经纬度上的直线距离的无量纲化倒数。

（3）经济—地理权重矩阵，即将含有距离因素与经济因素的空间单元引入权重矩阵，认为不同省域间变量的空间性关系不仅受到地理距离的影响，还会受到经济距离的影响，其中经济距离是指两个区域间经济发展的差距，用两个地区GDP差值的倒数表示。经济—地理距离是指在经济距离与地理距离的共同影响下，一个地区经济指标对周边地区影响的空间效应，权重矩阵中Wi，j为i与j地区经纬度上的直线距离的无量纲化倒数与GDP差值倒数的乘积。省市之间地理距离与经济距离越远则房地产泡沫空间溢出效果越差，所赋予的权重越小。预计系数α1、α2、α3符号为正，α2，α4，α6符号为负，ρ的系数为正，即房地产泡沫在区域间具有正向空间溢出性。表1-8结果显示，在空间滞后模型与空间误差模型中对数的似然函数值在经济—地理权重矩阵下优于0—1权重矩阵与地理权重矩阵，空间滞后模型与空间误差模型相比较指标显著性较高。本章选取以经济—地理作为权重矩阵的空间滞后模型，计量房地产泡沫的空间溢出效应，发现α1至α6的计量结果符号与预计相符，预期、宽松的货币政策（信贷量支持与较低的贷款基准利率）、人口密度的增加会刺激房地产泡沫的不断攀升；有效房地产供给的增加、非住房消费结构的优化，可以抑制房地产泡沫过快迅猛增长，各因素的作用下预期与供给因素对房地产泡沫的影响作用最强，分别达到0.842与-0.633。在0—1权重矩阵、地理权重矩阵与经济—地理权重矩阵下，房地产泡沫的空间溢出效应都为大于0的正值，说明一个区域的房地产泡沫的膨胀会有效带动周边地区泡沫值的攀升，空间影响系数为0.532。即一个地区房地产泡沫每增长一个百分点，会带动与他具有经济—地理关系地区房地产泡沫增长0.532个百分点。下文，笔者将进一步讨论各区域在2006—2016年，房地产泡沫的增长对周边具有经济—地理空间关系地区所产生的空间溢出效应，并对其空间溢出程度进行度量。

表1-8　各权重矩阵下的空间效应模型

注：***、**、*分别表示通过1%、5%、10%水平下的显著性检验，（）内为t值。