产业集中度的衡量方法及实现

一个产业内生产的集中程度可用各项产业（市场）集中度指标来衡量。这些指标的计算方法各一，所采用的统计口径也各有差别。迄今为止，较为常用的集中度指标主要有集中比率（Concentration Ratios，CR）、基尼系数（Gini Index，GI）和赫芬达尔-赫希曼指数（Herfindahl-Hirschman Index，HHI）等。集中度统计的范围通常为同属一个市场内的企业，不同市场的企业一般不能纳入同一项集中度统计之中。

1.绝对法

绝对法就是直接计算前几位厂商的市场份额，常用的绝对法计算指标有两个：前n位厂商的集中比率和赫芬达尔-赫希曼指数。

（1）集中比率

集中比率是指产业产出规模最大的前n家企业的合计产出占整个产业总产出的比重，它衡量的是一个产业中各企业产出分布的绝对集中程度。用公式可表示为：

式中，CRn为产出最大的前n家企业的产出集中比率，N为产业内全部企业数量，Xi为产出规模排在第i位的企业的产出。至于反映产出水平的指标X，则通常可在产量、生产能力、销售收入、销售量和产值等项指标中选择。另外，在集中比率计算过程中，n的选取并没有硬性的规定，完全根据特定研究的需要并结合特定产业的具体情况而定。

根据集中比率的大小，许多经济学家还提出过市场结构的相应分类。如贝恩在指出集中度是衡量市场结构的主要指标的同时，将美国制造业部门按集中比率的高低分作了六类：①极高集中型产业；②高集中型产业；③中高集中型产业；④中低集中型产业；⑤低集中（Ⅰ）型产业；⑥低集中（Ⅱ）型产业。

在计算集中比率时，有两个问题需要引起特别注意：第一，如果在同一产业内存在着一家母公司所控制之下的多家子公司，那么在统计时应将这几家子公司的相应数据合并计算。第二，对于多角化生产企业，在统计时应只计入属于同一产业的相应数据。

集中比率指标虽然因计算简便而常常成为衡量集中程度的首选指标，但它的一个主要缺点是集中比率指标不能精确反映产业内全部企业的产出规模分布结构。事实上，集中比率指标只是反映了整个产业最大的前几家企业的产出规模分布情况，即使这一指标可以反映市场结构的基本特征，也并不能完全揭示全部企业的产出规模分布结构。

（2）赫芬达尔-赫希曼指数

赫芬达尔-赫希曼指数是厂商市场份额的凸函数，对厂商之间市场份额的非均等分布非常敏感，该指数的定义为：

式中，X表示产业的总产出，通常以销售收入或销售量表示；Xi表示产业内第i家企业的产出，i＝1，2，3，…，N，与集中比率指标和基尼系数测算不同的是，所有企业可任意排列；Si为产业内第i家企业的市场份额。

显然，HHI指数值的分布区间为（0，1］。不过，在许多文献中，HHI指数值通常取的是（0，10 000］，即计算时不考虑百分比，其实际计算数值相当于采用式（5.2）方法所获数值的10 000倍，而此时其计算公式为：

HHI值越接近于10 000，表明集中程度越高；越接近于0，表明集中程度越低。当产业内只有一家企业时，HHI指数值为100的平方即10 000；当产业内所有企业规模相同时，由S1＝S2＝S3＝…＝SN可得HHI＝10 000／N。因此，在企业数量足够多的条件下，产业内企业规模越是接近，HHI值就越接近于0。

不仅如此，我们还可以引入企业市场份额方差，对HHI指数作进一步的分析。设一个产业内所有企业市场份额的方差为σ2，则有：

其中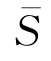为全部N家企业的平均市场份额，即S＝1／N，我们再设H为HHI指数值，则由式（5.4）可得：

因此，(www.xing528.com)

式（5.6）表明，市场份额方差的增大和企业数量的减少都会令HHI指数值上升，而市场份额方差的减小和企业数目的增加则会令HHI指数下降。就此而言，HHI指数显然能够同时兼顾产业内各企业规模的差异程度和企业数量，这一优点是集中比率和基尼系数所不具备的。

2.相对法

衡量市场集中度的相对法主要采用两种指标：一是洛伦兹曲线（Lorenz Curve）和基尼系数；二是厂商规模的对数方差。

（1）洛伦兹曲线和基尼系数

所谓基尼系数，是建立在洛伦兹曲线基础上的一个相对集中度指标。在产业组织学中，洛伦兹曲线被用来反映市场占有率与产业中由小到大企业的累计百分比之间的关系，而基尼系数则用以衡量同一产业内各企业产出的相对规模分布，即各企业产出规模的差异程度。如图5-1所示，横轴表示的是从规模最小企业开始的企业数量累计百分比X，纵轴表示的是这些企业的销售额（量）占市场总销售额（量）的百分比Y。而所谓洛伦兹曲线只是一条近似曲线，它实际上是所有（X，Y）点的连接线，因而可以反映产业内全部企业的规模分布状况。45°线为厂商规模分布的绝对平均线，亦即市场是一个均匀分布的结构（意味着20%的厂商占有20%的市场份额，40%的厂商占有40%的市场份额，依此类推），这时洛伦兹曲线与45°线完全重合。右下角的90°线为厂商规模分布的绝对非平均线，亦即独家垄断。处于45°和90°线之间的洛伦兹曲线代表了厂商规模分布的差异，是一条向下弯曲的曲线。如图5-1中的阴影部分下部的曲线所代表的厂商规模分布差异就比45°线的差异大，比90°线的差异要小。图5-1中的阴影部分的面积越大，厂商规模分布的差异就越大。

图5-1　洛伦兹曲线和基尼系数与厂商规模差异示意图

基尼系数就是洛伦兹曲线反映出来的特定市场中厂商规模的差异值，这是一种常用的绝对不均等的度量指标。基尼系数计算的就是洛伦兹曲线与绝对平均线（45°线）所包围的面积的比值，亦即。基尼系数越大，厂商规模的差异越大；反之，基尼系数越小，厂商规模的差异则越小。理论上基尼系数的取值范围是0≤GI≤1。

如图5-1所示，我们设全部企业数量为N，则每家企业占产业企业数量的比重为1／N；同时，设按照市场份额由小至大排序的企业序号为i，i＝1，2，3，…，N，第i家企业的市场份额为Si，且Si＞Si－1。因此，市场份额最小的前n位企业（n＜N）的累计市场份额即为。由均等分布线与洛伦兹曲线之间的面积（即图中阴影部分面积）等于均等分线与X轴和Y轴构成的等腰直角三角形面积减去洛伦兹曲线与X轴和Y轴构成的图形面积，可得基尼系数：

用基尼系数反映企业的规模分布结构及产业集中程度的优点是不言而喻的。首先，洛伦兹曲线直观并完全地揭示了产业内全部企业的规模分布状况，充分揭示了产业内各企业产出规模的差异，从而非常形象地表明了该产业产出的相对集中程度；其次，在企业数量足够多的情况下，由各产业基尼系数的比较所反映的产业之间集中程度的差距似乎更为可信。

当然，基尼系数也有着固有的缺点。其中最为突出的便是它无法真实反映各企业产出规模相似时的产业集中程度。特别是在企业数量较少时，基尼系数更常常会令人误解产业的集中程度。例如假定某产业内只有两家企业，且两者各自占有一半的市场份额，显然，这种典型的双头垄断产业的集中程度是极高的，其CR1为50%，CR2为100%，但若采用基尼系数计算，其数值竟为0，只是表明产业内所有企业规模相同，而根本无法说明产业的高集中程度。

（2）厂商规模的对数方差

厂商规模的对数方差为：

对数方差的最大特点是，假定厂商规模分布愈均匀，厂商之间的竞争性就愈强。

比较绝对法和相对法可得出如下的判断：绝对法主要反映了市场中前几家最大厂商的集中度，而未能考虑到参与整个市场的厂商数量和厂商规模的差异程度；而相对法则主要考虑到了参与整个市场的厂商规模的差异，却未能考虑到前几位最大厂商对市场竞争、价格等的控制和影响。两种方法各有利弊，单独一种方法都不能完全准确地反映市场中厂商之间的竞争程度，两种方法结合运用是比较全面的。

当研究具体产业的集中度时，究竟什么样的集中度才意味着一个产业既达到了规模经济又保持了有效竞争，至今仍是一个在经济理论和实践中均没有固定答案的问题。不仅不同产业的集中度由于产业的技术经济特点会有所不同，而且同一产业在不同时期的集中度也会处于不断变化之中。另外，同一产业在不同的国家也会表现出不同的集中趋势，这主要是与一国的经济发展程度、经济发展阶段、市场容量等相关，政府经济因素之外的考虑也对判断某一产业的集中起着一定作用，有时甚至是决定性的作用。