数学基础：等价无穷小、洛必达法则、重要极限、连续函数性质

1.(C)

【解析】等价无穷小、洛必达法则、变限积分求导.

由f（x）与g（x）为等价无穷小，可知

解得a＝3.

2.(E)

【解析】利用重要极限求解函数极限.

幂指函数求极限优先考虑是否为“1∞”型极限式，一般应用第二重要极限，将极限式化为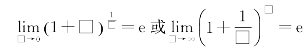的形式，再计算，故有

故

3.(D)

【解析】连续函数的性质.

反证法，若f（x）＋g（x）是连续函数，根据连续函数的性质，g（x）＝[f（x）＋g（x）]－f（x）也是连续函数，与题干条件矛盾，故f（x）＋g（x）不是连续函数，存在间断点，（D）项正确.

其余选项均可找出反例.令则（A）、（B）、（E）项均不正确；令f（x）＝x，则（C）项不正确.

4.(D)

【解析】函数在一点处连续的条件.

由题干可知函数在x＝0处连续，根据函数在某点连续的条件可得

所以，

5.(D)

【解析】导数的几何意义.

将x＝0代入方程，可得即y＝1.

对方程两边求导，则有ex－y（dx－dy）＋3（ydx＋xdy）＝0，将x＝0，y＝1代入得

所以，曲线在x＝0处的切线方程过点（0，1），斜率为1＋3e，故切线方程为y－1＝（3e＋1）x，即y＝（3e＋1）x＋1.

6.(D)

【解析】隐函数求导.

将x＝0代入方程，得y＝1.方程两边对x求导，可得

2xy2＋2x2y·y′－ex－y′＝0,

将x＝0，y＝1代入上式，解得

7.(E)

【解析】复合函数求导.

因为可知

f(0)＝2,f′(0)＝2,f′(2)＝e2,

故

8.(B)

【解析】一元函数极值.

因为y′＝3x2－12x＋9，令y′＝0，解得x＝1或x＝3，可知y的可能极值点为x＝1，x＝3.

又因为y″＝6x－12，所以y″（1）＝－6＜0，y″（3）＝6＞0，根据极值存在的第二充分条件，可知x＝1为函数的极大值点，极大值为y（1）＝0；x＝3为函数的极小值点，极小值为y（3）＝－4.

9.（A）【解析】构造函数、判断函数的单调性.

令F（x）＝exf（x），F′（x）＝exf′（x）＋exf（x）＝ex[f′（x）＋f（x）]＞0，则F（x）在（－∞，＋∞）上单调递增.

故F（1）＞F（0），即ef（1）＞f（0），排除（D）项；

F（1）＞F（－1），即e1f（1）＞e－1f（－1），则e2f（1）＞f（－1），（A）项正确；

F（0）＞F（－1），即e0f（0）＞e－1f（－1），则ef（0）＞f（－1）.

综上所述，本题选（A）.

【注意】本题关键点是构造函数.根据题干给出的条件，常见的函数构造如下：

①题干出现f（x）f′（x），则令F（x）＝[f（x）]2，有F′（x）＝2f（x）f′（x）.(www.xing528.com)

②题干出现f（x）＋f′（x），则令F（x）＝exf（x），有F′（x）＝ex[f（x）＋f′（x）].

③题干出现f（x）－f′（x），则令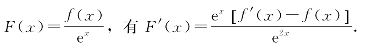

10.(B)

【解析】函数的极值、拐点问题.

（A）、（B）项：根据极限存在的第二充分条件：函数y＝f（x）在x0处二阶可导，且f′（x0）＝0，若f″（x0）＞0，则f（x0）是f（x）的极小值.

本题f″（x0）＝0，f‴（x0）＞0，则f′（x0）是f′（x）的极小值，故（A）项错误，（B）项正确.

（C）、（D）项：由于f′（x0）是f′（x）的极小值，且f′（x0）＝0，可知f′（x）≥0，即f（x）单调递增，f（x0）不是f（x）的极值，故（C）项、（D）项错误.

（E）项：因为f‴（x0）＞0，则在x0的邻域内f‴（x）＞0，故f″（x）在x0的邻域内单调递增.又f″（x0）＝0，则f″（x）在x0的两侧异号，根据凹凸性判定定理可知，（x0，f（x0））是y＝f（x）的拐点.

【注意】二阶导数为0，三阶导数不为0的点就是拐点.

28.(C)

【解析】齐次线性方程组解的性质、矩阵秩的性质.

由AB＝O，B≠O可知，Ax＝0有非零解，本题中A为方阵，故

可得λ＝1，0＜r（A）≤2，故r（B）≤3－r（A）＜3，即

【注意】也可以通过初等行变换法，准确求出r（A）＝1，故r（B）≤3－r（A）＝2，即

29.(C)

【解析】向量的线性表示.

因为α1，α2可由β1，β2线性表示，则r（β1，β2，α1）＝r（β1，β2，α2）＝r（β1，β2），故有

30.(B)

【解析】连续型随机变量的概率密度.

由连续型随机变量概率的计算公式，可得

31.(D)

【解析】概率的公式运算.

由，利用条件概率公式，可得又因为

故由加法公式得，

32.(D)

【解析】常见的连续型分布.

已知正态分布的密度函数关于X＝μ对称，已知P{X≤1}＝P{X≥5}＝0.3，故

33.(E)

【解析】数学期望的性质.

X～U（1，3），则Y～B（10，0.4），则E（Y）＝10×0.4＝4.

故由期望的性质，可得E（2X＋3Y）＝2E（X）＋3E（Y）＝2×2＋3×4＝16.

34.(E)

【解析】常见分布的期望和方差.

若随机变量X服从参数为λ的指数分布，即X～E（λ），则概率密度函数为f（x）＝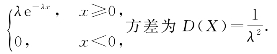

故X1～E（4），X2～E（2），，因为X1与X2相互独立，则

35.(C)

【解析】离散型随机变量分布律的性质.

根据分布律的正则性，可知

根据分布律的非负性，可知

【注意】本题也可通过概率的性质快速求解，令d＝4，此时a－d＜0，不满足概率的非负性，

排除（A）、（D）、（E）项，令d＝－4，a＋d＜0，可排除（B）项，故选（C）.