数学基础：等价无穷小与极限计算题

1.设函数，g（x）＝x3＋x4，若当x→0时，f（x）与g（x）为等价无穷小，则a＝（　　）.

(A)1　　(B)2　　(C)3　　(D)4　　(E)5

2.，则a＝（　　）.

3.已知f（x）在（－∞，＋∞）内连续，g（x）在x＝x0处间断，则下列说法正确的是（　　）.

（A）必为连续函数　　（B）g[f（x）]必有间断点

（C）f[g（x）]为连续函数　　（D）f（x）＋g（x）必有间断点

（E）f（x）g（x）必为连续函数

4.设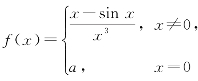在x＝0处连续，则a＝（　　）.

5.曲线在x＝0处对应的切线方程为（　　）.

(A)y＝(3e－1)x－1　　(B)y＝(3e－1)x＋1　　(C)y＝(3e＋1)x－1

(D)y＝(3e＋1)x＋1　　(E)y＝(3e＋1)x＋2

6.已知y＝y（x）由x2y2＋2－ex－y＝0确定，则

(A)e　　(B)1　　(C)0

(D)－1　　(E)－e

7.设函数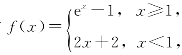则d{f[f（x）]}x＝0＝（　　）.

(A)0　　(B)edx　　(C)2edx

(D)(2e－2)dx　　(E)2e2dx

8.y＝x3－6x2＋9x－4，则下列说法正确的是（　　）.

（A）x＝1时，y有极小值0　　（B）x＝1时，y有极大值0

（C）x＝3时，y有极大值－4　　（D）x＝3时，y有极小值4

（E）x＝0时，y有极小值－4

9.设函数f（x）在（－∞，＋∞）上可导，且f（x）＋f′（x）＞0，则有（　　）.

(A)e2f(1)＞f(－1)　　(B)e2f(1)＜f(－1)　　(C)e2f(1)＝f(－1)

(D)ef(1)＜f(0)　　(E)ef(0)＜f(－1)

10.已知函数f（x）二阶可导，f′（x0）＝f″（x0）＝0，f‴（x0）＞0，则下列说法正确的是（　　）.

（A）f′（x0）是f′（x）的极大值　　（B）f′（x0）是f′（x）的极小值

（C）f（x0）是f（x）的极大值　　（D）f（x0）是f（x）的极小值

（E）（x0，f（x0））不是曲线y＝f（x）的拐点(www.xing528.com)

11.已知f（x）的一个原函数是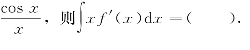

12.

13.

(A)22042　　(B)22042cos2　　(C)0

(D)2sin2　　(E)22042sin2

14.已知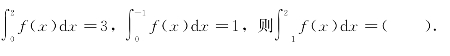

(A)0　　(B)1　　(C)2

(D)3　　(E)4

15.

16.设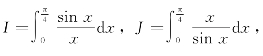则（　　）.

17.设f（x）为连续函数且满足关系式，则f（9）＝（　　）.

(A)　　(B)1　　(C)0　　(D)－1　　(E)3

18.设f（u，v）为二元可微函数，z＝f（sin（x＋y），exy），则

(A)f′1sin(x＋y)＋f′2exy　　(B)f′1cos(x＋y)＋f′2exy

(C)f′1cos(x＋y)＋yf′2exy　　(D)f′1cos(x＋y)＋xf′2exy

(E)f′1sin(x＋y)＋yf′2exy

19.已知z＝xesin（x－y），则

20.方程（x＋1）z－y2＝x2f（x－z＋y）确定函数z＝z（x，y），则

(A)－dx－2dy　　(B)－dx＋2dy　　(C)dx－2dy

(D)dx＋2dy　　(E)dx＋dy

21.z＝x4＋y4－x2－2xy－y2，则下列说法正确的是（　　）.

（A）（0，0）为极大值点　　（B）（0，0）为极小值点　　（C）（1，1）为极大值点

（D）（1，1）为极小值点　　（E）（－1，－1）为极大值点

22.函数f（x，y）＝x2＋xy＋y2－3x－6y，则函数（　　）.

（A）无极值　　（B）在（0，3）处取得极小值

（C）在（0，3）处取得极大值　　（D）在（3，0）处取得极小值

（E）在（3，0）处取得极大值