贝叶斯神经网络赋权的城市生活环境T-S模糊评价方法及其应用结果

1965年，美国加利福尼亚大学的控制论专家Zadeh.LA率先提出了模糊集合的概念。模糊综合评价是将模糊变换原理与最大隶属度原则运用到被评价事物的相关因素当中，进而对评价事物做出综合评价。其计算原理如式（8-12）所示：

其中，A为评价指标的权重经归一化处理得到的一个1×m阶矩阵，R为由各单指标评价行矩阵组成的一个m×n阶的模糊关系矩阵，B为综合评价结果，是一个1×n阶行矩阵的形式。

模糊理论的基础是隶属度函数的概念，其输出范围为[0，1]区间，而神经元的输出范围也在[0，1]区间，从而可以用来表现模糊集的隶属度，隶属度函数可以和模糊论结合起来。T-S模糊系统综合评价具有准确度高、算法快的特点，近年来随着机器学习的加速而得到广泛应用。本书引入T-S模糊系统对13个城市生活环境进行综合评价。

（一）T-S模糊系统

（1）在规则为Ri的情况下，模糊推理如下：

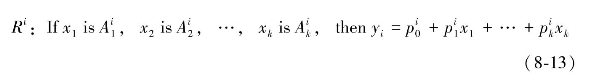
其中，为模糊系统的模糊集；为模糊系统参数；yi为根据模糊规则得到的输出。输入部分（即if部分）是模糊的，输出部分（即then部分）是确定的，该模糊推理表示输出为输入的线性绀合。

假设对于输入量x＝[x1，x2，…，xk]，首先根据模糊规则计算各输入变量xj的隶属度：

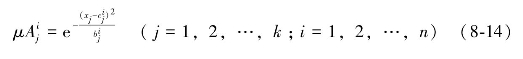
式中，分别为隶属度函数的中心和宽度；k为输入参数；n为模糊子集数。

对各隶属度进行模糊计算，采用模糊算子作为连乘算子：

根据模糊计算结果计算模糊模型的输出值yi：

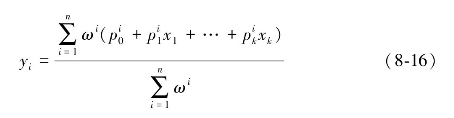
T-S模糊神经网络分为四个层次，即输入层、模糊化层、模糊规划计算层和输出层。输入层与输入向量xi二者相互连接，节点数与输入向量的维数相同。模糊隶属度值μ是通过模糊化层，采用隶属度函数对输入值进行模糊化得到的。模糊规划计算层采用模糊连乘公式计算得出ω。输出层采用公式计算模糊神经网络的输出。(www.xing528.com)

（2）模糊神经网络的学习算法如下所示。

①误差计算：

式中，yd是网络期望输出；yc是网络实际输出；e为期望输出和实际输出的误差。

②系数修正如式（8-18）与式（8-19）所示：

式中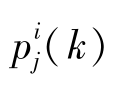，为神经网络系数；α为网络学习率；xj为网络输入参数；ωi为输入参数隶属度连乘积。

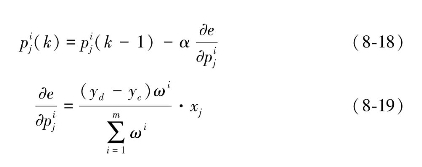
③参数修正：

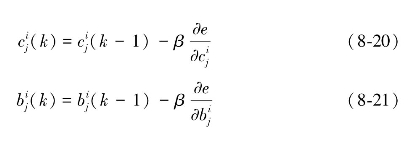
式中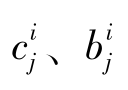，分别为隶属度函数的中心和宽度。

（二）T-S模糊神经网络的建立及评价结果

模糊神经网络的构建是根据训练样本维数来确定模糊神经网络输入/输出结点数、模糊隶属度函数个数。采用归一化的训练样本和检验样本数据，对网络进行训练和检验，再利用已训练好的模糊神经网络对城市生活环境竞争力进行综合评价，得到的结果与排名如表8-13所示。

表8-13　T-S模糊神经网络法得分及排名

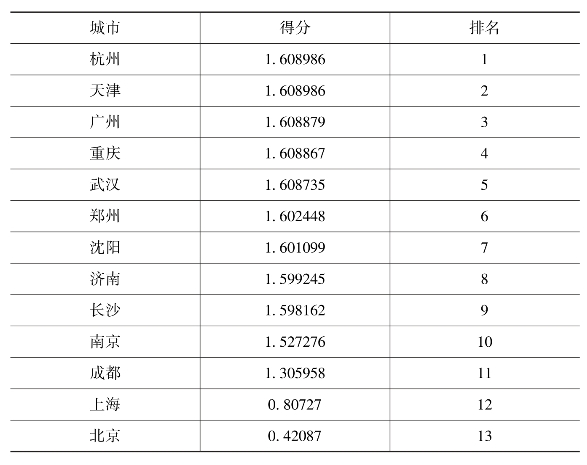
通过比较以上五种综合评价的结果可以得出，各种评价方法的结果不尽相同，同一个城市在不同的评价方法中所得到的评价得分是不同的，单从主观上也无法判断哪一种评价方法的评价效果优良，因此需引入科学的检验方法对评价效果进行验证。