基于原始数据的城市生活环境评价方法：基尼系数的应用

（一）基尼系数理论及方法介绍

基尼系数（Gini Coefficient）是客观反映收入分配不均程度的数量界限，是由意大利经济学学家基尼（Corrado Gini）于1992年提出的。本书旨在运用基尼系数的原理对城市生活环境进行评价，这样既可以考虑到指标的公平性，还可以考虑到效率性，这有利于对城市环境竞争力进行综合评价。

张菀洺（2013）测算了教育公平的基尼系数，并选用联合国的标准作为判断教育公平程度的限值，得出我国的教育公平状况出现明显的好转；胡祖光（2004）在收入五分法的前提下，通过严格的数学公式推导得出基尼系数的理论最佳值为1/3；田平和秦迪岚分别利用基尼系数研究了洞庭湖和张家港水网的水污染物总量分配问题的优化，并将0.2作为基尼系数的合理限值，本书采取的标准也是按照联合国的基尼系数划分标准。

城市环境竞争力的评价是一个复杂的过程，在前文的论述中已经进行了原始指标的筛选，并利用神经网络得到了各个指标的权重分布，接下来利用基尼系数的方法结合前文得到的权重进行综合评价。本书之所以用基尼系数进行综合评价，除了基尼系数本身的优点之外，主要有以下六个原因。

一是城市环境竞争力评级体系复杂，应该保证评价体系的客观性。从目前的研究方法来看，其主要的综合评价方法有主、客观两大类。主观的方法一般有Delphi法、AHP、G1、G2、模糊综合评判法等，这类评价方法大多根据经验进行赋值计算，其主观性较强，人为因素较大。客观赋权法有熵权法、主成分分析法、TOPSIS法、灰色关联度法等，这类方法中的原始数据由各指标在被评价对象中的实际数值形成。这些常用的方法都在某些方面存在一定的缺陷。

二是无法保证数据信息的敏感性，以及信息贡献的累积过程，从而无法体现评价过程的公平性问题。

三是利用基尼系数最大限度地消除了量纲化的影响。这是因为基尼系数计算的本身就已经消除了指标之间的单位量纲，利用基尼系数进行两两计算，可以更好地反映指标之间的差异性，最大限度地使用数据所反映的信息量。

四是基尼系数的使用范围最广泛。李刚（2014）在对基尼系数进行研究时发现，不论数据经过何种无量纲化处理，运用基尼系数都可以很好地进行评价，该种方法不受限制，但是其他的评价方法均在不同程度上有所限制。^[3]

五是保序性比较好。保序性优良的标准是比较在不同数据形式下的权重大小并进行排序，一致性的顺序越多，则认为这种方法的保序性越好。李刚通过实证证明了基尼系数方法在保序性上具有极其优良的特性。

六是基尼系数在反映贫富差距上具有优势——全球通用，因此用这种方法得到环境竞争力的基尼系数再进行评价，其合理性就更高了。具体如表8-7所示。本书还将结合13个城市的指标数据进行实证分析。

表8-7　不同方法在不同数据形式下的适用性检验表

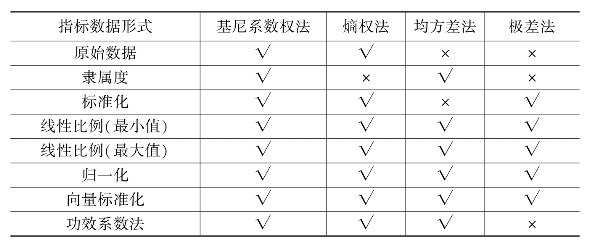
注：“√”表示适用；“×”表示不适用。

基尼系数的计算方法有很多种，其主流的方式一般包括：直接计算法、几何法、协方差法、平均差法、矩阵法、曲线回归法、人口等分法、城乡分解法。这些方法在不同的情境下，其选择方式也均不相同，每种计算方法的误差也不同。本书简单介绍几种常用的基尼系数计算方法。

基尼在1912年提出了无替换的基尼平均误差计算公式：

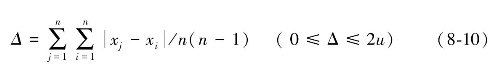
其中，Δ是基尼平均差；是任何一对样本差的绝对值；n是样本容量；u是收入均值。

通过上式可以发现，Δ是收入不平等程度的单调递增函数，于是基尼规定G＝Δ/2u，0≤Δ≤1，所以直接计算的基尼系数的表达式为：

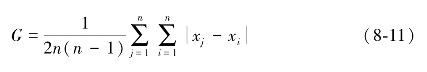
但是理论的计算方法在真实情况中却很难应用，因为这种计算方法对于数据的要求很高，要求收入的数据不仅仅可以获得，而且还要具有代表性，并且当样本趋于无穷时，其运算量很大。虽然原始的计算方法的误差很小，但是在现实中直接使用该公式的情况较少。

回归曲线法是常用的基尼系数的计算方法。这种方法适合于样本数据较少、OC曲线未知的情况。其计算根据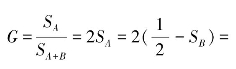1－2SB，具体的步骤如下。

第一步，设定洛伦兹曲线的函数关系式，一般设为幂函数OC＝αpβ。

第二步，利用样本数据进行拟合回归，计算出α、β的参数值。若进行幂函数的拟合出现R方的数值较小，则可以换其他的函数进行模拟。利用其他函数的模拟，其计算思路与幂函数的积分求解思路相同，但是求解的最终结果与第三步的G的计算不同。

第三步，求积分计算出基尼系数值G，即：

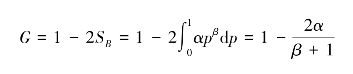
（二）基尼系数法的具体计算

对于本书而言，由于数据量较小，并且均为离散的数据，所以对于直接求解法则不能使用。另外，本书借鉴了基尼系数方法的兼顾评价体系公平性和效率性的特点，并选用了该方法。因此，书中对于环境竞争力的评估并未涉及人口、收入等因素，所以也不宜使用城乡分解法。因此，本书计算的基础建立在回归拟合法的基础之上，其方法和步骤均与上文的介绍相同。

本书所选用的计算公式以及方法如下所示。

第一步，计算与分析单项指标基尼系数。这里主要包含：①首先把经济综合竞争力指数（简称ECCI）与各个指标进行比值计算，然后进行升序排列；②计算出各个指标的累计值和累积百分比；③根据坐标（0，0），…，（1，1）等绘制洛伦兹曲线。

第二步，根据公式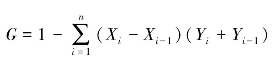，进行回归拟合，其中Xi为年平均气温、城市绿化覆盖率、人口密度、污水处理厂集中处理率、等效声级、空气质量好于二级的天数、人均城市道路面积、市辖区人均GDP这8个指标。Yi为经济综合竞争力的累积百分比，i为分配对象，当i＝1时，（Xi－1，Yi－1）视为原点坐标（0，0），这样求出的是某一个指标的13个城市的整体的基尼系数。

第三步，计算某一个城市的单一指标的基尼系数。(www.xing528.com)

（1）计算累积基尼系数（AG），Gi表示单一指标的整体基尼系数，APk是指在升序排列的前提下，第k个城市单一指标的累积百分比，所以，AGk＝Gi×APk。

（2）计算第k个城市的第i个指标的单一基尼系数，这里设为Gki，则Gki＝AGk＋1－AGk。

第四步，计算综合基尼系数。综合基尼系数用字母CG表示，其计算公式为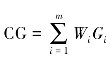：，其中Wi为第i个指标的权重。这里所使用的权重为上文中利用神经网络训练得到的权重，且满足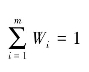，Gi表示第i个指标的基尼系数。对于这里直接使用的神经网络训练的权重，前文已经进行了详细的叙述，不再赘述。

第五步，根据最终的数值进行综合评价，并对结果进行具体分析。评价分为两种：一是利用整体基尼系数进行整体评价，二是利用某一城市所有指标的基尼系数与权重的乘积进行城市评价。

由于基尼系数可以克服量纲化的影响，所以不论是使用原始数值还是量纲化后的数据均可。由于前面使用的是利用极值法进行的标准化，这种形势下每种指标标准化后的数据必定含有0。但是计算基尼系数的过程中需要指标标准化后的数据作为分母，所以这里不可使用对极值法进行标准化的数据。因此，该部分采用原始数据进行测算基尼系数。

（三）基尼系数的测算过程

这里主要包含三个步骤：第一步，把经济综合竞争力指数（ECCI）与各个指标进行比值计算，然后进行升序排列；第二步，计算出各个指标的累计值和累积百分比；第三步，根据坐标（0，0），…，（1，1）等绘制洛伦兹曲线，然后通过曲线拟合，找到拟合效果最好的曲线，利用曲线函数进行求解积分，得到单个指标的基尼系数。每个指标的求解过程，如表8-8及附表21～附表27所示，其中每个表格第9列的数值即为单一指标的最终基尼系数。表格的第10列根据公式Gki＝AGk＋1－AGk进行计算而得。这里仅以年平均气温-环境竞争力基尼系数表（表8-8）的第10列进行详细论述。该表的第2行第10列的数值即为累积基尼系数的数值；第3行第10列的数值为0.0551，是由第3行第9列的数值减去第2行第9列的数值得到的结果。第10列其他的数值以此类推，分别得出杭州、济南、北京、上海等城市的单一指标的基尼系数，本章中只有年平均气温基尼系数表，如表8-8所示，剩余7大指标的基尼系数表如附表21～附表27所示。

为了进一步地分析问题，我们进行了数据整理。整理的原因就在于，起初在进行洛伦兹曲线拟合的过程中有一个必要的环节，就是计算比值。比值即为表8-8及附表21～附表27的第2列的数值除以第3列的数值，从而得到比值这一列。按照洛伦兹曲线的求解过程，必须按照比值的大小进行城市升序排列，可以得出，表8-8及附表21～附表27中的第1列的城市排列顺序均不同，其原因就在于比值这一项在不同指标下的大小排列顺序不同。其他表格的计算过程与此相同，不再赘述。

表8-8　年平均气温-环境竞争力基尼系数

续表

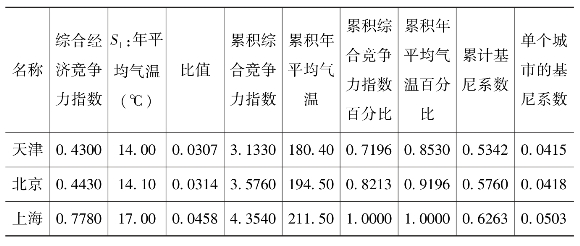
注：根据前面的叙述，单一指标的整体基尼系数即为基尼系数那一列的最后一个数值。如平均气温-环境竞争力最终的基尼系数即为0.1868.最后一列表示每个城市在平均气温-环境竞争力下的基尼系数。

为了更好地观察这些不同城市不同指标的基尼系数，本书对数据进行了重新的整理，表8-9中的S1～D11是按照原始城市排序以后的数据结果，表的最后一列是加权-城市基尼系数。

表8-9　最终排名基尼系数及其整理数据

在利用神经网络的过程中得到S1、S5、S10、P7、P16、R11、D5、D11的权重值分别为0.0827、0.1158、0.0635、0.0638、0.2496、0.1086、0.2055、0.1105。利用公式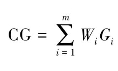进行求解，其中表格的第2行第10列的数值计算过程是：

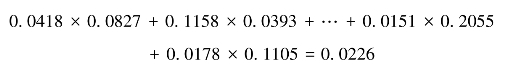
其余的第10列数据以此类推即可。所有城市的单一指标的综合基尼系数和加权-城市基尼系数如表8-9所示。

关于拟合优度的问题，可以说洛伦兹曲线的拟合效果的好坏，很大程度上影响了基尼系数的误差的大小。在对洛伦兹曲线进行拟合的过程中，选用线性、二次函数、三次函数、幂函数、对数函数等函数进行测试，并进行拟合效果的对比，最终选用的是对比后拟合误差最小的函数形式。其函数的参数如表8-10所示。

表8-10　各种方程的拟合参数

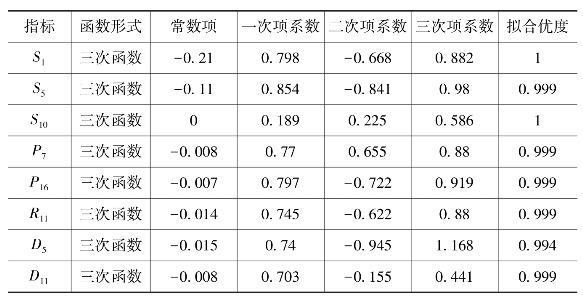
从表8-10中可以看到，利用三次函数进行拟合优度的检验效果很好，在进行R方检验的时候竟然趋近于1，这说明曲线的拟合效果极好。但是这里有必要说明一下为什么进行拟合的函数的效果都会集体性地趋向1。在进行求解基尼系数的过程中，必须先计算比值，然后对比值进行升序排列，然后再进行累计。因为，进行排序以后，数据就变得不再杂乱无章，加之进行累计才可以拟合曲线，由于数据是从小到大地进行累计，而每一个城市的每一种指标的数值差距又不是极大，所以，其累计过程刚好符合幂函数、三次函数的变化过程。按照一般意义上的拟合函数，幂函数应该被采用，本书也进行了幂函数的拟合，其中R方均在0.9以上，效果也比较理想。但是三次函数的拟合效果比幂函数的效果更好，所以这里采用前面所讲的计算过程的例外情况，选择了非幂函数的其他函数，并且给出了拟合效果很好的原因。

表8-11　综合基尼系数

通过计算综合基尼系数可以看出各个指标的整体基尼系数，前文已经交代了对于综合基尼系数的分析是建立在国际基尼系数的临界值上的。在贫富差距的衡量中，选用0.4这一数值作为衡量临界值，超过0.4，则认为贫富差距较大。借鉴这一说法，本书对综合基尼系数进行分析，发现只有S1年平均气温和S5城市绿化覆盖率这两个指标的综合基尼系数超过0.4，这说明在城市生活环境竞争力的评价中，S1与S5这两个指标是亟待提升的指标，但是从指标的本身属性上看，年平均气温是无法或者说很难改变的，每个城市所属的气候不同，存在很大的差异。所以，降低S5指标的综合基尼系数对于提升我国城市生活环境竞争力水平十分重要。另外，虽然其余的6个指标的综合基尼系数均小于0.4，但是S10与D5的数值均十分接近于0.4，所以，在提升S5的同时也应该关注这两个指标的综合基尼系数的变化。

计算每个城市的加权基尼系数，并根据系数的大小得到每个城市最终利用该方法得出的城市生活环境竞争力排名。将基尼系数法与Borda法进行比较，具体如表8-12所示。

表8-12　加权基尼系数法与Borda法的最终排名

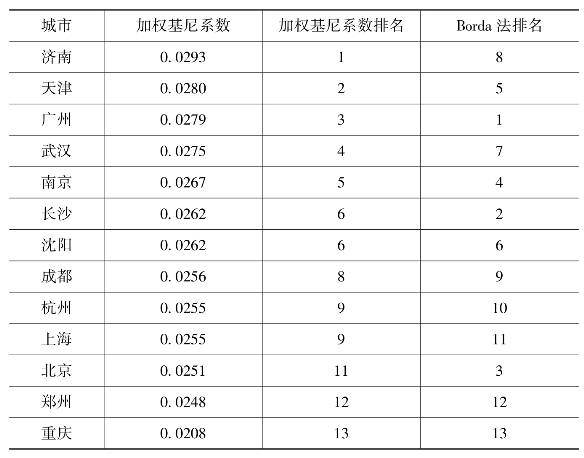
通过数据可以得出基尼系数法与Borda法对于城市生活环境综合评价的排名，其运行的结果整体相同，差距较小。其中济南、北京、长沙三个城市的评分排序差距较大，其余的排名的差距均小于3，其中对于南京、沈阳、上海、杭州、郑州、重庆等城市的排名相差无几，但是依然需要对两种方法的评价结果的优良性作出比较。