在结合前文所选的13个城市和8个指标，分别运用熵权法给各指标进行赋权，在运用TOPSIS法和主成分分析法对13个城市进行综合评价和排名的基础之上，为了综合上述两种评价方法的优点，建立Borda模糊组合评价模型，并运用该模型对13个城市生活综合竞争力重新进行综合评价和排序，使其结果更趋于合理。
（一）综合评价方法的差异性（一致性）分析
上述两种评价方法的评价对象虽然是同一组数据，但由于评价方法的原理不同，使得最终的排名也不尽相同。为了进一步了解评价方法是否存在差异性或一致性，采用相关样本的非参数检验来验证这两种评价方法的差异化程度，判断其是否存在显著的差异性。若不存在显著的差异性，则再使用相关系数检验法判断两种评价方法的密切程度，以及两种评价方法的具体得分及排名结果。
相关样本的非参数检验是在对总体分布不太了解的情况下，对样本所在的相关配对总体的分布是否存在显著差异性进行检验，该检验一般是对同一研究对象分别给予多种处理，判断各处理方法是否存在显著差异性。虽然该检验对单个总体的分布并不做过多要求，但必须是成对的数据，通过比较对应样本之间的差异来检验总体的差异。
结合本书实际，选用适合两相关样本非参数检验的Wilcoxon秩和检验。结合两种评价方法的Wilcoxon检验结果可以得知两种评价方法得分之间差异的中位数不等于0，即二者存在一定的差异性。
如附表19所示，由Wilcoxon检验可知二者存在差异，那么为了进一步了解二者存在的相关关系，本书再运用Pearman等级相关系数来求解二者的相关系数，如附表20所示。综合Wilcoxon检验和Pearman等级相关系数检验可知，两种评价方法并不趋同，存在一定程度的差异化，为了更好地利用以上两种评价方法，需要对这两种方法进行改良，使之更趋于合理。
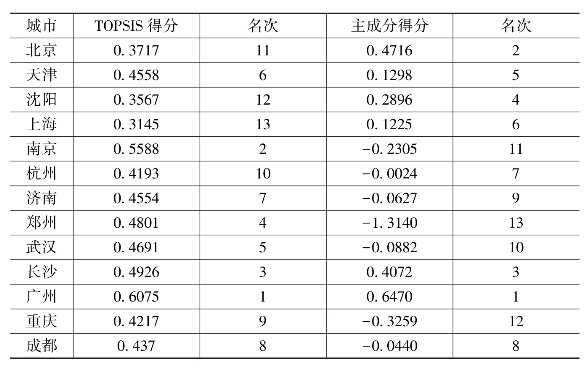
表8-3 两种评价方法的得分及排名表
（二）建立组合评价模型——模糊Borda组合评价模型
从上述两种单一评价模型的排序结果来看，二者存在一定的差异。为了消除这种差异，充分利用单一模型的优点而尽量避免单一模型的缺陷，本书采用模糊Borda组合评价模型[1]重新进行综合评价，借以得出更为合理的结果。模糊Borda在综合以上两种评价模型时既能考虑到二者得分上的差异，又能充分考虑排序上的差异。[2]具体的计算过程如下所示。
第一步，令μij为城市i在第j种评价方法下属于“优”的隶属度，其计算公式为：
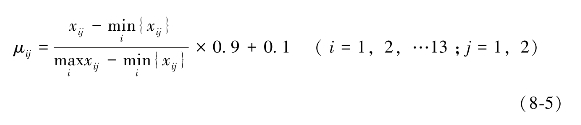
其中，xij为城市i在第j种评价方法的具体得分，结果如表8-4所示。
表8-4 两种评价方法下的隶属度
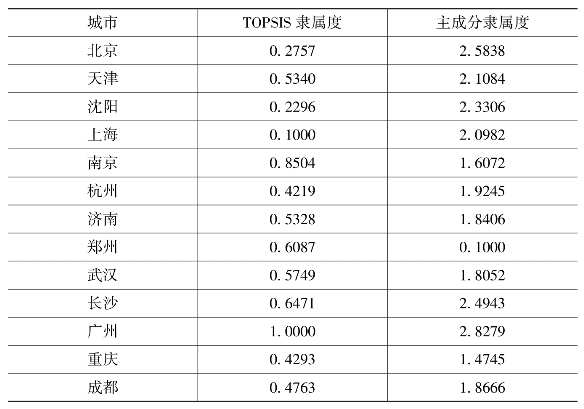
第二步，令pih为城市i排在第h位的模糊频数，计算模糊频数（率），具体结果如表8-5所示，其公式为：
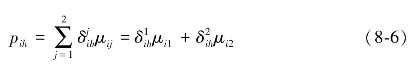(www.xing528.com)
其中，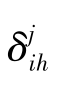
为城市i在第j种评价方法下排在第h位，则有：
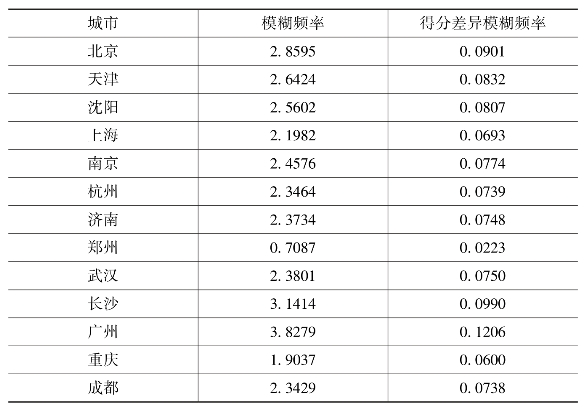
表8-5 模糊频率及得分差异模糊评价表
其中，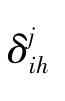
为城市i在第j种评价方法下排在第h位，则有：
定义反映得分差异的模糊频率为：
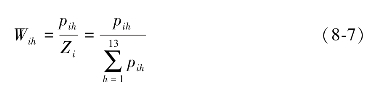
第三步，令Qh为城市排在h位的得分，将其排序转化为得分，其公式为：
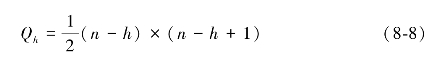
其中，1≤h≤n。
再令Bi为城市i的模糊Borda数得分，计算公式为：
其中，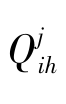
为城市i在第j种评价方法下排在第h位的得分。最终可以得到模糊Borda综合评价得分及排名，如表8-6所示。
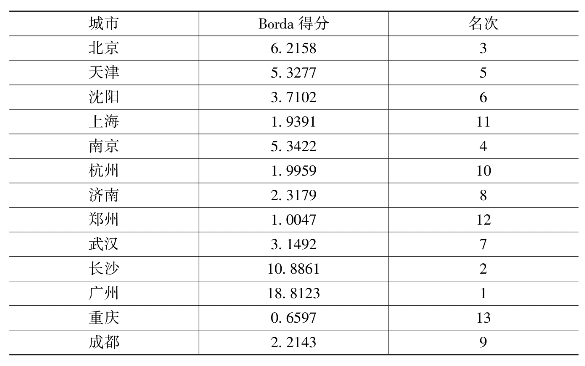
表8-6 模糊Borda综合评价得分及排名表
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
