城市生活环境评价的主成分赋权结果

主成分分析法是一种客观赋权的评价方法，其中心思想就是利用降维将原有的多个指标线性组合成新的指标，在降低指标间重复信息的同时还保留了大部分（80%以上）的原始信息，而且其客观性体现在各指标的方差贡献率就代表了综合评价的权重，减少了人为赋权的主观因素干预，主成分综合评价在常见的综合评价方法里具有简单、易于操作的特点。主成分评价有以下五个步骤。

第一步，原始数据标准化处理，直接使用上一部分TOPSIS法标准化后的数据Y。

第二步，计算第一步得到的数据集Xij的相关系数矩阵R。

第三步，计算特征值及单位特征向量，即计算R的特征值（λj，j＝1，2，…，8）及其对应的单位特征向量。

第四步，计算主成分的方差贡献率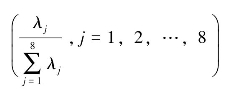和累计方差贡献率。

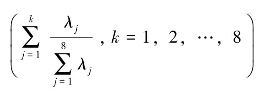第五步，计算主成分。(www.xing528.com)

由附表15可知，前4个主成分因素的累计贡献率达到了80.497%，大于80%，因此，选择4个主成分已足够。同时还得到了因子载荷矩阵（ajl），如附表16所示。

因子载荷矩阵并不是主成分分析中所需要的标准化正交向量（ejl），为了得到标准化正交向量，还需对因子载荷矩阵做进一步的处理，计算公式为：，得到标准化正交向量矩阵ejl，如附表17所示。

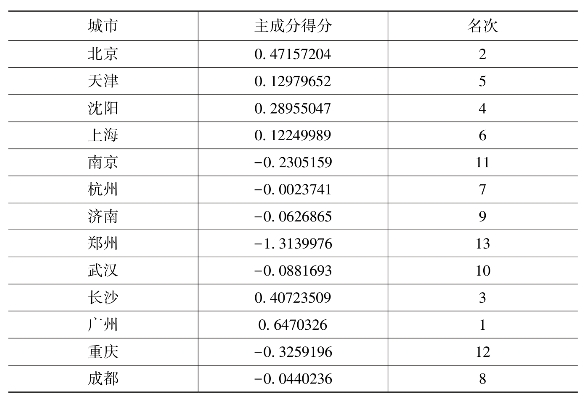
利用标准化后的矩阵Y与标准正交特征向量矩阵ejl得到前4个主成分，计算公式为：f＝Y×ejl。以每个主成分的方差贡献率作为权重构造评价函数，算出13大城市的综合得分并排名，如附表18所示。计算函数为：F＝0.28065f1＋0.22945f2＋0.19264f3＋0.10223f4。可得综合得分及排名如表8-2所示。

表8-2　城市生活评价主成分得分及名次表