贝叶斯正则化神经网络权值的初始化一般是随机产生的,这期间会有很大的误差,不同的权值会对最终的结果有很大的影响,因此本书结合熵权法取初始权值进行训练,以减少初始权值对最终结果的影响。一般情况下,神经网络初始训练参数是根据经验值设定的,期间有很大的误差,本书根据数据训练输入参数,将训练结果作为权值训练初始值输入。
(一)城市生活环境评价神经网络随机赋权
第一步,将原始数据13×8矩阵的第一行数据分别乘以其对应的8个权重w1k(k=1,2,…,8),得到一组1×8的矩阵,作为新的矩阵的第一行。再将该矩阵分别加上对应的8个权重w1k(k=1,2,…,8),得到一组1×8的矩阵,作为原始数据矩阵第二行的权重,记为w2k(k=1,2,…,8)。
第二步,将原始数据13×8矩阵的第二行数据分别乘以其对应的8个权重w2k(k=1,2,…,8),得到一组1×8的矩阵,作为新的矩阵的第二行。再将该矩阵还是分别加上对应的8个权重w2k(k=1,2,…,8),得到一组1×8的矩阵,作为原始数据矩阵第三行的权重,记为w3k(k=1,2,…,8)。
第三步,重复上述过程分别在上一行的基础上算出新的矩阵,最终得到一个全新的13×8矩阵。
第四步,将新矩阵每列相加,分别记为q1j(j=1,2,…,8),最终得到一个1×8的矩阵。
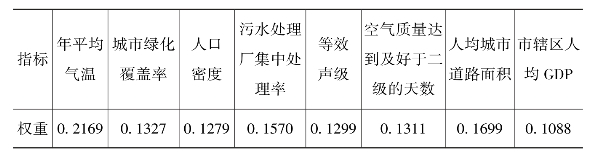
第五步,将第四步得到的1×8矩阵求和得到求和值,将求和值与阈值相比较。如果求和值小于阈值,则通过检验;如果求和值大于阈值,则说明参数设置不合理,需重新设置参数。根据以上步骤,神经网络随机赋权结果如表7-1所示。
表7-1 神经网络随机赋权结果
(二)城市生活环境改进熵权法赋权结果(https://www.xing528.com)
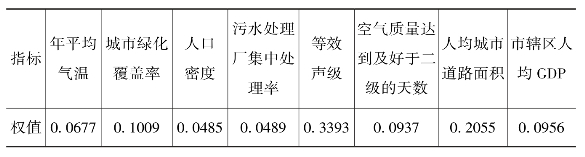
通过计算,熵权法权值如表7-2所示。
表7-2 熵权法训练权值表
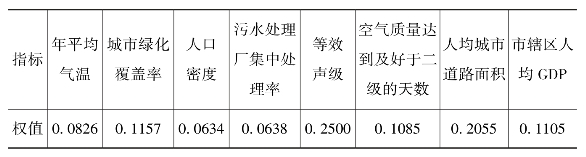
通过计算发现有奇异值,因此采用改进的熵权法重新计算的权值如表7-3所示。
表7-3 改进熵权法训练权值表
(三)贝叶斯正则化神经网络权重结果
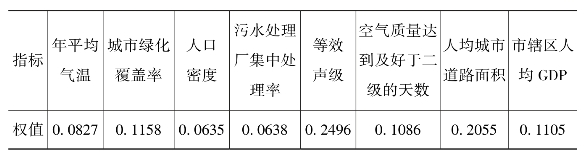
采用贝叶斯正则化算法(trainbr)训练误差值,最终训练出的允许误差结果为0.00053959。将之前计算的熵权法作为神经网络的初始权值输入,将贝叶斯训练误差值输入,结合神经网络训练出的权重结果如表7-4所示。
表7-4 贝叶斯正则化神经网络权值表
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




