基于L1和H1/4改良的神经网络参数赋权算法及其应用

标准的BP神经网络算法应用中，网络训练很容易形成局部极小而得不到全局最优，在训练过程中发生震荡、收敛变慢。目前主要是通过改进动量因子、学习率可变的方式修改神经网络。

动量BP算法是在梯度下降算法的基础上引入动量因子η（0＜η＜1）。

本算法的具体操作过程是，以前一次修正结果影响本次修正量，当前一次的修正量过大时，第二项的符号将与前一次修正量的符号相反，从而使本次的修正量减少，起到减少震荡的作用。当前一次的修正量过小时，第二项的符号将与前一次修正量的符号相同，从而使本次的修正量增大，起到加速修正的作用。

对于学习率可变的BP算法，学习率在整个学习过程中起到很大的作用。因其是常数，当学习率过大时，算法可能震荡；当学习率过小时，则收敛的速度较慢，训练时间长。因此需要利用局部误差来调整学习率，有：

因为训练函数traungdx和learngdm各有各的优缺点，因此可以在MATLAB的选择参数中将二者结合起来并利用各自的优点。

除此之外，本书还主要进行初始参数的优化，其目的是使输出结果尽量合理。因此引出了下文熵权法和贝叶斯改进算法的应用。

（一）L1概述

在前一章筛选出的8个指标中，除年平均气温和人口密度不能使用正负向指标数值表示，其他的都可以使用正负向指标数值表示，因此需要转化为正负向指标来表示，以便后续的计算。故引入了L1范数来进一步衡量指标。

L1范数是指向量中各个元素的绝对值之和，也有个美称叫“稀疏规则算子”（Lasso regularization）。范数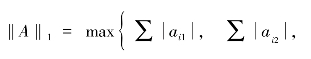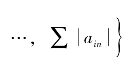：（列和范数，A为每一列元素绝对值之和的最大值，其中为第一列元素绝对值的和，其余类似）。

在泛函分析中，范数表示的是一个“长度”概念的函数，为向量空间内的所有向量赋予非零的正长度或大小。

（二）H1/4熵权法叙述

在具体的实验操作过程中，通过研究发现，直接使用熵权法得到的权重常常会出现某个数值很大的情况，这与指标重要性的程度严重不符。在多指标评价过程中，尽管各指标的重要程度不尽相同，但若某个指标的权重过大，则通过该指标就可直接反映被评对象的优劣，而无需考虑其他指标。正是因为如此，熵权法的应用受到了一定限制。鉴于此，本书将以0.25为上限，并且以神经网络训练权重，以求进一步减少其误差。^[2]

（三）熵权法改良赋权模型构建

在信息论中，熵是对不确定性的一种度量。熵权法是依据各指标数据所包含的信息量大小来确定指标的权重，信息量越大，则熵越小，反之则越大。^[3]

其中，xi为第i个状态值（总共有m个状态）；P（xi）为出现第i个状态的概率。根据熵的特性，可以通过计算熵值来判断一个事件的随机性及无序程度，也可以用熵值来判断某个指标的离散程度，指标的离散程度越大，该指标对综合评价的影响（权重）越大，其熵值越小。(www.xing528.com)

设有m个城市待选评价，n项选择指标的指标数据矩阵为X＝（xij）m×n，对于某个指标，j为待选供应商的指标值Xij间的差距越大，信息熵就越小，该指标在选择中所起的作用就越大，赋予的权重就越高；反之就越小。

第一步，指标的归一化处理：异质指标同质化。

由于各项指标的计量单位、性质属性并不统一，因此，对于不同指标用不同的算法进行数据标准化处理。其具体方法如下。

正向指标：

负向指标：

第二步，计算第j项指标下第i个城市占该指标的比重：

其中，k为比例数，一般认为是结果，取k＝（Inm）－1。

计算指标的差异系数，由上式计算可得第j个指标的差异系数hj：

第三步，计算第j项指标的熵值：

第四步，计算信息熵冗余度：熵权修正。

当wj＞0.25时，将其强制修正为，将多余部分wj－0.25通过下式按比例分配到其余m－1个指标中。

由此得出各指标的修正熵权。

若W*中又出现某个指标的修正熵权，则可将其强制修正为0.25，再将多余的部分权重根据上式分配到其余的m－2个指标中去，然后得到m－2个指标的修正熵权。

通常而言，如果所得指标的熵权超大，将其修正后，一般不会再出现一个指标的熵权大于0.25的情况。