(一)熵权法
熵权法主要是基于信息论中的信息有序性提出的一种指标权重确定方法。某个评价指标数据的有序度关系到信息量的多少,信息熵越小,对于评价数据所提供的信息量也就越大,在对指标赋权的时候,就应该赋予较大的权重,基于该原理,熵权法被提出来,并用于指标权重的确定。熵权法主要根据评价数据的有序度来确定指标权重,但是由于熵权法是基于确定性信息来计算的,对于不确定性信息,需要经过一定的数据转换后才能采用熵权法来确定指标权重。熵权法确定权重的主要过程如下:
第一步,设影响评价结果的因素集有m个,对n个待评价对象的综合评价矩阵经过规范化后的矩阵为R=(rij)n×m,其中rij表示对第i个待评价对象的第j个指标下的评价值。对矩阵R=(rij)n×m按列进行归一化,即得到归一化后的矩阵: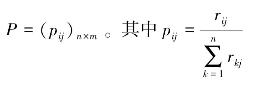 。
。
第二步,计算熵权。计算第j个评价指标Cj(j=1,2,…,m)的熵值为:
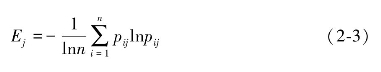
则此时有0≤Ej≤1(j=1,2,…,m),从而可以计算出指标Cj的熵权为:
![]()
第三步,确定指标权重。根据评价指标权重满足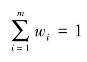 ,对熵权进行归一化后,即可得到最终的评价指标的权重向量:
,对熵权进行归一化后,即可得到最终的评价指标的权重向量:
W=(w1,w2,…,wm)
其中: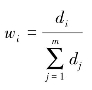 。
。
(二)主成分赋权法
主成分赋权法主要是基于多元统计分析的原理来给出权重的一种指标赋权法。主成分赋权法根据评价数据进行主成分分析,先计算每个指标下评价数据的相关矩阵,再对相关矩阵计算特征值,并最终确定指标的权重。主成分赋权法主要是基于指标评价数据的相关性来确定指标的权重,该方法对指标的个数没有限制。
主成分赋权法的主要过程如下:
第一步,采集数据。设评价指标集为C1,C2,…,Cm,评价方案集为A1,A2,…,An。设对第i个方案的第j个评价指标下的评价值经过标准化处理后为xij,则经过标准化处理后的评价矩阵为:

第二步,计算相关系数矩阵。记第i个评价指标的评价向量为Xi=(x1i,x2i,…,xni)T,则第i个评价指标的评价向量均值为![]()
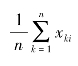 ,计算第i个评价指标下的评价数据Xi与第j个评价指标下的评价数据Xj的相关系数:
,计算第i个评价指标下的评价数据Xi与第j个评价指标下的评价数据Xj的相关系数:
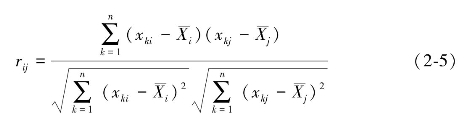
其中,i,j=1,2,…,m,从而可以得到m个评价指标之间的相关系数矩阵为R=(rij)m×m。
第三步,计算主成分。计算相关性矩阵R=(rij)m×m的特征值λi及其对应的正交特征向量ξi=(ξi1,ξi2,…,ξin),其中满足λ1>λ1>…>λm≥0。分别计算贡献率和累计贡献率。
贡献率为:

累计贡献率为:

当累计贡献率δp≥0.85时,则对应主成分个数为p。
第四步,计算指标权重。选择前p个特征值λ1,λ2,…,λp,对应的正交单位特征向量 ξ1=(ξ11,ξ12,…,ξ1,m)T,ξ2=(ξ21,ξ22,…,ξ2,m)T,…,ξp=(ξp1,ξp2,…,ξp,m)T,则对应的主成分权重为:
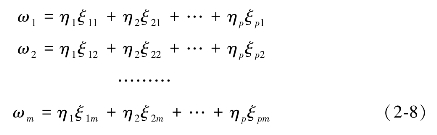
对主成分权重进行归一化处理,即可得到最终的评价指标的权重向量:
W=(w1,w2,…,wm)
其中: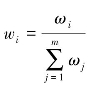 。
。
(三)优化赋权法
优化赋权法主要是在获取评价数据和指标权重大概区间的基础上,设计一定的优化指标构成非线性优化模型,最后采用一定的计算方法来获取评价指标的权重。这类方法中最常用的有离差最大法。使用该方法获得的权重依赖于评价数据,如果评价数据出现变化,则对应的指标权重也会改变,因此,该方法得到的指标权重仅适用于当前评价数据,而不能将该权重作为恒定的指标权重。
设评价指标集为C1,C2,…,Cm,评价方案集为A1,A2,…,An。对第i个方案的第j个评价指标下的评价值经过标准化处理后为xij,则经过标准化处理后的评价矩阵为:

设待确定的指标权重向量为:W=(w1,w2,…,wm),且指标权重向量满足约束条件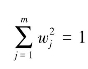 。
。
为确定评价指标的权重,针对第j个评价指标Cj,方案Ai的指标加权值与方案Ak的指标加权值的离差为:|wjxij-wjxkj|。则可以计算得到方案Ai的指标加权值与其他所有方案的指标加权值的离差和为:(https://www.xing528.com)

依次计算每个方案与其他所有方案在评价指标Cj下的离差和,从而可以得到所有方案与其他方案在评价指标Cj下的总离差和为:
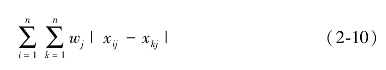
上面只分析了所有方案与其他方案在评价指标Cj下的总离差和,只包含指标Cj的指标权重信息。
一般在确定指标权重的过程中,希望每个方案的指标加权评价值与其他所有方案的指标加权评价值的离差尽可能的大,以有效降低综合评价过程中各方案评价值的分歧程度,使综合评价结果更为合理。因此,构造如下确定指标权重向量的目标函数:
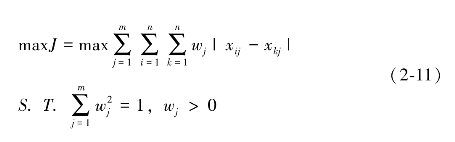
对于该非线性目标函数,基于多元函数极值原理,通过求解最终可以确定出最优解为:
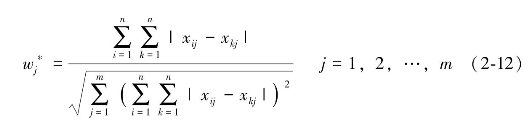
对最优解进行归一化处理后,即可得到基于离差最大化的指标权重向量:
W=(w1,w2,…,wm)
其中,
(四)灰色关联度赋权法
灰色关联度赋权法是一种主要根据每个指标下的评价数据与预设的比较数列之间的灰色关联度来确定指标权重的方法。灰色关联度主要刻画两个向量构成的曲线的几何贴近度,一般与比较序列的灰色关联度越小,对应指标的权重越小。灰色关联度赋权方法已经广泛用于综合评价之中,但有限定条件的约束。
设对n个方案进行评价,需要确定m个评价指标的权重向量。设经过标准化处理后的评价矩阵为X=(xij)n×m。其中xij为第i个方案在第j个评价指标下的标准化评价值。下面给出基于灰色关联度的指标权重确定方法,以第i个评价指标下的n个方案的评价值Xi={x1i,x2i,…,xni}为参考序列,其余m-1个评价指标下的n个方案的评价值向量:
Xj={x1j,x2j,…,xnj}(j=1,2,…,m,j≠i)
计算比较序列Xj={x1j,x2j,…,xnj}与参考序列Xi={x1i,x2i,…,xni}的第k个元素的灰色关联度系数,如式(2-14)所示。
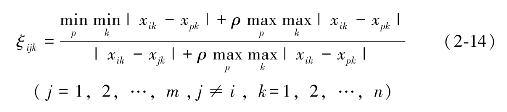
其中,待识别参数ρ∈[0,1],常取ρ=0.5。则比较序列Xj={x1j,x2j,…,xnj}(j=1,2,…,m,j≠i)与参考序列Xi={x1i,x2i,…,xni}之间的灰色关联度为:
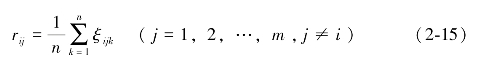
依次令i=1,2,…,m,即依次令X1={x11,x21,…,xn1},X2={x12,x22,…,xn2},…,Xm={x1m,x2m,…,xnm}为参考序列,其他指标下的评价向量为比较序列,得到各指标之间的灰色关联度矩阵如表2-5所示。
表2-5 不同参考序列下的灰色关联度矩阵
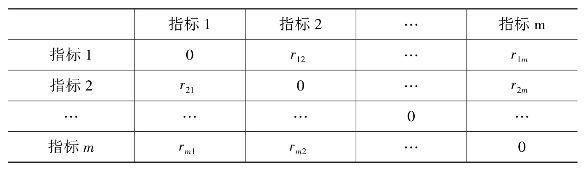
则每个指标与其他指标的评价相关度为:
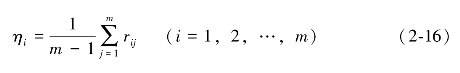
对每个指标的相关度进行归一化后,即可得到m个评价指标的权重向量为:
W=(w1,w2,…,wm)
其中, 。
。
(五)变异系数赋权法
变异系数赋权法主要是将每个评价指标下的评价数据看作样本集,分别计算每个评价指标下的样本集的均值和标准方差,根据标准方差与均值的比值得到该评价指标下评价数值的变异系数,最后对变异系数进行归一化,得到的数值即为每个评价指标的权重值。变异系数赋权法主要是基于统计学的原理,根据方差与均值之间的变异情况来体现指标的重要性。
设对n个方案进行评价,需要确定m个评价指标的权重向量。设经过标准化处理后的评价矩阵为X=(xij)n×m。其中xij为第i个方案在第j个评价指标下的标准化评价值。具体如下:
第i个评价指标下的方案评价值构成的评价向量为Xi={x1i,x2i,…,xni},i=1,2,…,m。依次计算向量Xi的均值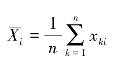 和标准差
和标准差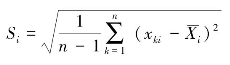 ,则可以得到第i个评价指标下各方案评价值的变异系数为:
,则可以得到第i个评价指标下各方案评价值的变异系数为:
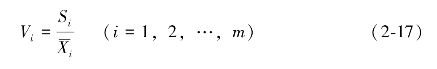
对变异系数进行归一化处理,即可得到最终的m个评价指标的指标权重向量:
W=(w1,w2,…,wm)
其中,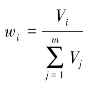 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




