随机前沿生产函数用于采掘业的模型检验及LR统计检验

本书采用随机前沿生产函数的方法，模型是否适用首先需要进行检验。传统生产率研究都使用平均生产函数，衡量企业生产率水平的高低，要素的产出弹性为平均值，该方法忽略了生产无效率因素对生产的影响（张各兴，2011[107]）。若生产无效率项U iτ不存在，那么模型就成了简单最小二乘估计，随机前沿参数失去作用，模型变成了平均生产函数模型。

检验模型是否合适的方法是检验γ（技术无效率所占的比例）的值，γ取值越接近于1，则前沿生产函数的误差项主要来自随机变量；γ越接近于0，则实际产出与最大可能产出的差距主要来自可控制因素，这种情况不适合采用随机前沿分析模型。γ越显著接近1的取值则越适合采用随机前沿分析模型。根据本书模型检验结果，γ值达到0.999，其t值为2 342 331，说明生产无效率在采掘业中普遍存在，采用随机前沿生产函数是合适的。

然后模型进行LR统计检验。LR检验又称混合卡方检验（mixed chi-square distribution）。在计算出LR值后，笔者通过和混合卡方检验的临界值进行比较，大过临界值说明通过检验。LR统计量可以表示为：

公式中L（H 0）和L（H 1）分别为前沿生产函数在原假设和备择假设下的似然函数值和）分别是对β（参数集合）、σ2（误差项方差）的极大似然估计。

如果约束条件成立，则相应的约束模型与非约束模型的极大似然函数值是近似相等的，这是LR检验的基本思路。其中LR统计量服从自由度为n的混合卡方分布（自由度n为原假设H 0中零参数约束的个数）。LR统计检验的原假设以及检验结果如表6-1。(www.xing528.com)

表6-1　LR统计检验的原假设及检验结果

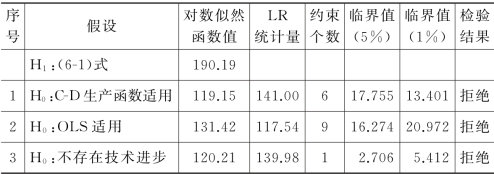
注：临界值为5%和1%显著水平下的混合卡方分布，见Kodde.David A.，Franz C.Palm.1986.“Wald Criteria for Jointly Testing Equality and Inequality Restrictions”，Econometrica，54，p.1246 Table 1。
资料来源：作者制表。

原假设1：假设在生产函数形式上，β4=β5=β6=β7=β8=β9=0，即Cobb-Douglas生产函数要优于超越对数生产函数。在1%的显著水平下，原假设被拒绝，说明超越对数生产函数更适用，若采用Cobb-Douglas生产函数形式，则会产生较大的误差。

原假设2：假设所有样本省份的采掘业生产均处于生产前沿面上，随机误差项所代表的技术非效率影响为零。如果原假设成立，即γ=ξ1=ξ2=ξ3=0，则用普通最小二乘法（COLS）估计出来的平均生产函数可以很好地描述样本的生产过程，此时无需采用SFA方法来估计函数形式。同样，在1%的显著水平下，原假设被拒绝，说明模型中技术非效率是显著存在的，样本均处于生产前沿下方，采用COLS得到的平均意义上的生产函数不适用于本研究。

原假设3：假设不存在技术进步，即β10=0，结果显示在1%的水平上被拒绝。

以上检验说明，模型通过了LR检验，适用性较强。下面进行实证分析。