能源效率模型分析与估计的方法及省际随机前沿分析模型

在关于生产要素需求的实证研究中，一般以新古典经济学所假设的利润最大化或成本最小化为起点来推导需求函数，不考虑市场失效问题。但是，如果外部性问题、价格管制或者市场竞争不充分等因素使关于生产者行为的上述假设不成立，基于该假设估计的要素需求函数往往是有偏的和不一致的。中国对能源商品长期实行价格补贴和价格管制，生产者和消费者对能源的实际支付价格往往低于竞争市场形成的价格；即使是那些定价机制已基本市场化的能源商品，价格也没有反映资源利用和环境影响的外部成本。价格扭曲使市场信号不能正确传递给生产者，造成生产中对能源的过度使用。过度使用意味着要素投入是非效率的，导致关于生产者的利润最大化或成本最小化的行为假定不能成立。Debreu（1951）和Farrell（1957）进行了关于生产效率的开创性研究。前者提出了基于产出方向的技术效率衡量方法，后者提出了基于投入方向的效率衡量方法，被统称为Debreu-Farrel效率（Kumbhakar，2000），即以生产边界作为效率衡量基准，如果给定产出的所有投入无法同比例减小，或者给定投入的所有产出无法同比例增加，则称为生产有技术效率（technical efficiency），否则存在技术非效率（technical inefficiency）。Debreu-Farrel效率因与其对应的效率径向测度方法使用便利而成为生产效率分析的基本框架。投入距离函数可表示为：D I（y，x）=max{λ≥（1：x）|λ∈L（y）}，其中y表示产出，x代表投入向量。L（y）=（x∈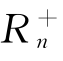：y∈R+）。投入距离函数反映给定y时x的最大径向缩减程度。对于任何可行产出，D I（y，x）≥1。若x在生产边界上，则D I（y，x）=1；x在生产边界之内，则D I（y，x）＞1，表明生产中存在技术非效率。

设距离函数为超越对数函数形式，它作为一般函数的二阶近似，其形式灵活，无太多假设条件并考虑了变量间的交互作用。Colli和Perelman（1999）建立了多产出、多投入的投入距离函数，根据他们的研究，在单一产出、多投入的生产情形下，距离函数可表示为：

方程（6-1）除满足ln D I（y，x）≥0之外，还要满足如下齐次线性和对称性条件：

根据齐次线性条件，方程（6-1）可以转化为：

再在方程（6-3）中引入统计误差v it，令，则：

方程（6-4）即Aigner等人（1977）提出的随机前沿函数的基本形式。若将能源要素作为等式左端的投入要素X j，则有：

将方程（6-5）转化为：(www.xing528.com)

方程（6-6）构成一个关于能源投入的随机前沿模型，其中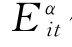代表实际能源投入，f（·）是从生产技术角度建立的能源需求函数，是能源投入的确定性前沿部分，它提供了衡量有效能源投入的基准，代表在前沿技术水平和产出水平既定时，由生产决策和其他外部因素决定的最小能源投入。Y it和X it是生产决策变量，Y it代表产出，X it代表能源之外的其他生产要素，Z it为其他外部影响因素，β为确定性前沿的参数变量。

根据Debreu-Farrel效率，本章将确定性前沿作为衡量基准，产出既定时，若生产中实际能源投入大于前沿上的能源投入，则视为存在因技术非效率而造成的过度投入；将通过消除技术非效率而能够减少的能源投入界定为节能潜力。由于在SFA中实际观测误差为混合误差（u it+v it），需将非效率影响从中分离。根据以往的分解方法，能源投入效率和节能潜力分别表示为：

方程（6-7）中，E（·）表示条件期望，Eff it表示能源投入效率，即有技术效率的前沿投入与实际能源投入之比，方程（6-8）表示可以实现的节能潜力。

根据方程（6-6）可以得到：

随机误差影响u it服从均值为0、方差为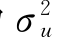的正态分布。非效率影响u it由线性回归模型（6-9）来解释，z it是由关于非效率的解释变量构成的向量，δ是参数向量。u it服从在0处截断、均值z itδ、方差为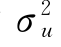的单侧正态分布。为使εit与u it的假设分布一致，εit服从均值为0、方差为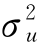的断尾正态分布，截断点为-z itδ（Battese和Coelli，1995[111]）。

在此模型理论基础上，下面针对采掘业的能源效率进行分析，建立省际层面的随机前沿分析模型。