数据预处理在土地用途分区中的研究成果

空间数据挖掘的数据预处理又可以称为数据清理(data cleaning)、数据清洗(data cleaning)、数据净化(data scrubbing)，是解决原始数据中存在的空缺值、孤立点、噪声数据等数据质量问题的一项技术。数据质量问题是数据源中普遍存在的问题，如果不能有效地解决数据中存在的这些数据质量问题，就无法高效、准确地从事数据挖掘工作，甚至产生错误的结果。因此，为了获取更好的土地用途分区的结果，减少数据挖掘内核的工作量，提高数据挖掘的精度，必须进行土地用途分区数据清理。王树良(2006)、樊敏(2009)已经对既有的空间数据挖掘的数据预处理进行了比较系统的总结和研究，结合研究的问题，主要针对土地用途分区中的空间数据和属性数据的预处理进行研究。

1.空间数据

由于1∶1万土地数据库中的图斑数目庞大而且十分破碎，若以现状图斑为基本单元则计算效率将十分低下。在土地现状库建库的时候，图斑不是以地类为外围边界的。在同一个连续的大片地类中，由于权属、田坎、小渠道和其他一些自然界线的存在，在野外调绘的时候把它们分为几个图斑来看待，如彩图5-5所示，虽然在区域内仅有4个地类(林地、基本农田、园地和居民点)，但是从图上可以看出中间的大片林地是由很多图斑组成的，其实这些图斑之间都是属于林地，只是属于不同的地块或权属，在进行野外调绘的时候被分隔为很多小的图斑。对于这些图斑，在进行分区前必须要进行一定程度的合并，考虑到本实验的情况，通过空间距离和图斑的拓扑关系对具有相同属性图斑进行合并，具体通过拓扑关系判断：

规则5.1：if LandUT1＝LandUT2 and S1＞20 and S2＞20 then LandUZP＝LandUT1

该规则可以理解为如果两个图斑的现状地类是相等的，且面积均大于20公顷，那么两个图斑进行合并。

2.属性数据

不同部门不同来源的数据由于各部门需求不同，可能存在重复采样的情况，经过数据集成后的集成数据库容易出现数据冗余的现象，冗余的数据不仅不能保证一定能比精简的数据获得更好的结果，反而会加重计算过程中不必要的开销，引起资源浪费。模糊概念格只能处理离散型数值，必须将连续型的数据离散化并转换为可以用模糊概念格表示的多值背景。主要采用冗余属性剔除和连续属性离散化两种数据归约技术。

(1)冗余属性剔除

进行数据集成后，如果直接用模糊概念格进行关联规则挖掘，可能会带来大量的问题，考虑到属性间可能彼此之间存在某种关联，某一个属性可能蕴含了其他的属性，各数据源之间属性命名不一致也可能导致集成数据集中的冗余。由于空间叠置分析产生碎多边形等问题也会导致数值之间的冗余，于是剔除相关冗余信息是对土地利用数据集成后遇到的首要问题。

相关分析是通过相关系数，又称皮尔逊积矩系数(pearson product coefficient)来度量两个数值指标之间的相关关系，因此，在冗余属性剔除工作中，可以使用相关分析来检测冗余程度，通过相关分析来度量两个属性之间的蕴含情况，相关系数计算公式为(Jiawei Han et al.，2001，2007)：

式中，N为记录个数；ai和bi分别代表第i个记录的A与B的值；分别代表A与B的均值；σA、σB分别代表A与B的标准差。

式中rA，B的值域为[-1，1]，如果rA，B为正数，则意味着A与B正相关，A的值随着B增加而增加，该值越大，则代表属性之间的蕴含关系越强；如果rA，B等于0，则表明因子A与B相互独立，不存在相关关系；如果rA，B小于0，则代表A与B负相关，一个值随另一个的减少而增加，也就意味着每个因子都阻止另一个的出现。由此可知，在计算相关系数后，可以将相关系数较高的两个因子之中的一个作为冗余因子来剔除。

(2)属性离散化(www.xing528.com)

现实生活中的许多数据均是连续值，而许多成功应用于数学挖掘领域的算法均只能处理离散数据，在进行挖掘之前，必须对数据进行离散化。因此，在进行挖掘任务之前，也面临着连续属性离散化的问题。离散化就是选取断点来对条件属性的取值空间进行划分，使得条件属性的取值变成有限的子区域的过程。离散化也是一个可以有效提高算法效率的数据预处理方法，而且使用离散的数据，可以帮助人们对分类规则的理解。

离散化是指将数值属性的值域划分为若干子区间，每个区间对应于一个离散值，最后将原始数据更新为离散的区间。根据离散化是否使用分类属性信息可将连续属性离散化方法分为无监督离散化和有监督离散化两种。其中无监督离散化方法不使用分类属性信息，只考虑自身属性取值的特点，这种方法相对较为简单，等宽度间隔、等频率或等深间隔均属于无监督离散化方法；而有监督离散化的方法是结合自身属性取值情况与分类属性取值情况，采用一定的衡量标准来划分属性取值子空间的一种方法。

目前连续属性离散化的方法有许多，并各具特色。应用最为广泛的离散化方法是基于信息熵(D.K.Y.Chiu et al.，1990；J.Catlett，1991；Usama M.Fayyad et al.，1993；鄂旭等，2005；谢宏等，2005)、基于统计学的方法(Kerber，1992；Huan Liu et al.，1997)和Rough集理论(H.S.Nguyen et al.，1995；H.S.Nguyen，1998；苗夺谦，2001；赵军等，2002；周艳聪，2004)的离散化方法。各种离散化方法各有优缺点，在实际应用时，需要根据具体的问题选择有效、合理的离散化方法。

由于研究中对连续属性离散化的目的是为了进一步分类挖掘，因此选用有监督的离散化方法比无监督离散化方法更为合适，选择离散化算法也必须充分考虑离散化后的结果能够最大程度的保持数据的原有信息，对数据子区间进行合并的依据必须合理，ChiMerge算法是一种经典的有监督的、自底向上的自动化离散化方法，它使用χ2统计来衡量要离散的属性两个相邻区间基于分类属性信息数据分布的相似程度，以对多个区间的质量进行分析。因此，选用ChiMerge算法对土地利用数据库中的连续属性进行离散化，对某个属性的多个区间的质量进行分析，如果χ2的检验结果表明分类属性的信息独立于属性的区间，那么区间就应该合并，否则就表示区间之间的统计差别很大，不能进行合并(Mehmed Kantardzic，2003)。

根据相关文献(Kerber，1992；Mehmed Kantardzic，2003)，结合土地利用空间关联规则挖掘的特点，可描述基于ChiMerge的土地利用连续属性离散化具体算法步骤为：

第一步：对已知属性的数据进行升序排列，并获取属性取值的值域；

第二步：根据属性取值的值域定义初始区间，使得该属性每个属性取值均独立成为一个区间；

第三步：计算任意相邻区间的χ2值；设土地利用类别为p类，该连续属性任意两个相邻区间的χ2检验由下式确定：

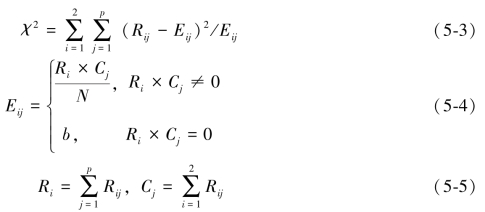
式中，p为分类个数；Ri，j为第i个区间第j类实例的个数；Ei，j为Ri，j的期望频数；b为一常数，可取0.1，这样做的目的是为了避免检验数的分母太小；Ri为第i个区间实例的个数；Cj为第j类实例的个数；N为两区间总实例个数。

第四步：获取所有χ2中的最小值，假设为min，并判断该最小值min是否小于给定阈值，若小于，则将这两个相邻区间合并；否则，重复第二、第三步，直至任何两个相邻区间的χ2都大于给定的阈值。

第五步：判断离散化后的区间数是否小于自定义的最大值，如小于，则输出合并结果，否则合并不可行，增大阈值，返回第二步，直至满足最终结果。

在土地利用数据中，不会仅仅只有一个属性为连续属性，往往需要对一个以上的属性进行离散化，这时应该分开定义每个属性的最大区间数的阈值和χ2检验的置信区间。当属性的取值范围较多时，其阈值应该取较大值以免离散区间数太多。