改进抗体-抗原亲和度函数以优化混沌免疫克隆选择算法

如何基于空间关系与属性指标一体化的空间对象模型建立新的空间-属性混合距离测度，并纳入空间聚类计算模型，真正反映出类内“属性相似，空间相近”，类间“属性相异，空间相离”的空间分类规则(王艳等，2009)，还需开展深入研究。基于空间-属性一体化的思想，用混沌免疫克隆选择算法进行空间聚类计算，充分挖掘空间坐标和空间关系数据中隐含的空间聚集信息。

土地用途分区就是将待聚类的图斑在约束条件下，在相关知识的指导下，对数据集进行的划分，划分的好坏需要进行衡量，在传统的聚类算法中使用相似性进行度量。相似性度量是指选定能够衡量模式间亲疏关系的指标体系的过程。一般用模式对间的距离函数来定义其相似关系，但也有其他方式。例如，在基于模型的聚类方法中，构成某个类别的相似性标准就可能使模式符合特定的统计模型。即使采用距离函数，针对不同问题、不同的数据类型、不同的聚类方法采用的距离评价标准往往也各不相同。在混沌免疫克隆选择算法中可以使用抗体-抗原亲和度进行衡量，这可以通过构造空间聚类的目标函数来实现。

1.空间聚类的目标函数

作为数据挖掘的一种有效工具，聚类分析在土地用途分区领域常常需要处理大量高维数据集，作为分区的对象——图斑的属性不但包含了数值型数据，还包括了大量的类属型数据。解决这一问题的方法可以使用传统的将类属值转化为数值的方法，但是事实证明这不是一个有效的办法，主要原因是类属域是无序的。只有很少几种算法能较好地处理混合属性数据聚类问题，例如k-原型算法等，但这些方法同样要求聚类类别数c和聚类原型的先验知识。

(1)数值型数据聚类的目标函数

高新波(1999)使用的聚类目标函数如下：

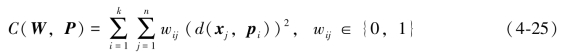
式中，pi＝[pi1，pi2，…，pim]T表示第i类的原型，wij是目标xj属于第i类的隶属度。W是k×n阶的划分矩阵，且满足概率约束；∀j，d(·)是定义为距离的相异性测度。像土地利用图斑这样具有实特征的数据集，即X⊂Rm，则有：

因为wij是样本xj属于第i类的隶属度，当wij∈{0，1}时，称W是硬k-划分。在硬划分中，wij＝1表示样本xj属于第i类。

高新波提出的目标函数是针对数值型数据进行聚类分析用的，在土地用途分区中，有数值型的，也有很多是类属型的，比如地类代码、用途等属性是属于类属型数据，这一目标函数就很难对其进行描述，因此应该研究能够同时处理类属型和数值型数据的混合数据聚类的目标函数。

(2)混合数据聚类中的目标函数

土地利用图斑的属性包含了几十甚至上百个属性项，具有混合特征，也就是说这些属性项既有数值型的也有类属型的，如果某一样本用表示，则混合类型数据xi和xj之间的相异性测度可以用下式计算：

式中等号后边的两项分别代表数值特征上的距离测度和类属特征上的测度。δ定义为：(www.xing528.com)

为避免偏向任何一种特征，使用权值λ用来调节两种特征在目标函数中所占的比例。当λ＝0时，聚类仅仅取决于数值特征；当λ＞0时，可以看到不完全取决于数值特征，随着λ的增大，聚类的结果更多地取决于类属型特征，因此这也是要得到的结果。彩图4-7是土地现状图的部分，可以表示这一原理。对该区域进行分区，如果仅使用距离目标函数来进行聚类(当λ＝0时)，那么两个用途区的分界线就应该是中间的平直界线(用虚线表示)；但是把图斑的属性信息也考虑进来的时候(λ＞0)，聚类的结果就不完全取决于空间距离了，这时图斑1将会被分到左边的林地中，图斑2将会被分到右边的基本农田中；当λ越大，4、5号图斑也有可能被分到林业用地区中，3、6、7号图斑可能被分到基本农田保护区中。这在简单地以空间距离为目标函数的聚类中是很难理解的，但是土地用途分区是可能存在的，因为土地用途分区不能保证每个区都只有一个，而可能是由多个互不相连的区组成的。

为了研究具有混合属性特征数据的聚类问题，首先定义一种新的距离测度函数，将不同属性特征相结合，从而达到具有混合属性特征的数据进行聚类分析的目的。对于混合类型的目标，为得到新的目标函数，可以对式(4-25)中的相异性测度进行修正，从而得到新的目标函数。高新波提出的模糊聚类问题，进一步可以修正目标函数为：

令，可将公式(4-29)改写为：

对具有数值和类属混合特征的数据集进行模糊聚类分析时，式(4-30)就是其目标函数。为了保证聚类的效果，目标函数C(W，P)需要达到极小化，可以通过分别极小化和来达到目的，因为二者均是非负值。

2.抗体-抗原亲和度的构建

由目标函数的定义可知，目标函数的大小决定着聚类的效果。因此目标函数越小，抗体-抗原亲和度应该越大，聚类效果也越好。因此，如式(4-31)所示，可以借助目标函数来构造抗体-抗原亲和度。

3.抗体-抗原亲和力

针对约束优化问题，按如下方式定义抗体-抗原亲和力：引入一个概率Pf，其值可以是通过随机产生，也可以是通过自适应的方式产生，如果以概率1在待求解的可行解空间内将问题的目标函数值作为抗体-抗原亲和力；在待求解的非可行解空间内以概率Pf、1-Pf将目标函数和惩罚函数做归一化处理，并将产生的值作为抗体-抗原的亲和力使用这种概率型的亲和力计算方式，可以达到平衡目标函数和惩罚函数的目的。这样，两个抗体中某个抗体具有较高亲和力(胜出)的概率为：

式中，可以定义Pφw是当前抗体因惩罚函数值而胜出的概率；Pw是当前抗体因目标函数值而胜出的概率。仅当两个抗体都同时为可行解时，某个抗体胜出的概率Pw＝Pfw。