混沌免疫克隆选择算法的性能优化

美国著名气象学家洛伦兹最早创立了混沌理论，他认为混沌是随机发生的而实际上其行为却是由精确的法则决定的一种过程。混沌广泛存在且敏感地依赖于初始条件的内在变化，是相对于一些“不动点”、“周期点”的特定形式的一种未定形的交融于特定形式间的无序状态。混沌有着精致的内在结构，是一种“奇异吸引子”，在特定的范围内能把系统的运动吸引并束缚(黄润生，2005)。混沌的发现，对科学的发展具有空前深远的影响，并在许多领域得到了应用。混沌具有其独特的性质：①初值敏感性，即初始条件的微小差别最终将导致根本不同的现象；②遍历性，即在一定范围内混沌能够不重复地经历的所有状态；③规律性，即混沌是由确定性的迭代式产生的。

针对混沌具有遍历性这一特点，可将其作为搜索过程中避免陷入局部极小的一种优化机制，如果利用混沌变量进行优化搜索，无疑会比随机搜索更具优越性。因此，混沌已受到广泛重视和大量研究，并成为一种新颖的优化算法。其思想是利用混沌运动所具有的特点使混沌搜索在一定范围内能按照其自身的规律不重复地遍历每一个状态(黄润生，2005)。混沌优化算法分两个阶段进行：①在变量的变化范围内依次遍历所经过的各点，并以较好点作为当前最优点：②以当前最优点为中心，施加混沌扰动，进行细致搜索寻找最优点。混沌优化方法思路直观，编程实现简单方便，已有的研究成果表明是一种良好的优化方法(K.Aihara，1990)。混沌优化方法虽然具有对初值敏感、易跳出局部极小、搜索速度快和全局渐进收敛等优点，但在搜索空间较大时其效果并不显著。目前已经产生了很多与其他智能算法相结合的算法：如混沌神经网络(K.Aihara，1990)、混沌遗传算法(郭子龙，2005)、混沌免疫遗传模糊算法(G.C.Liao，2004)等。

经典的克隆选择算法搜索解空间的主要方法是通过克隆变异算子完成对最优解解临近空间的搜索，本质上这种搜索是通过空间的扩张与压缩，将局部搜索和全局搜索结合起来实现问题的求解，有效地利用了待求问题中的一些有用信息，克服了进化算法中早熟收敛，从而可以达到抑制优化过程中产生的退化的目的，跳出局部极小值的约束。研究表明，克隆变异后个体的质量直接决定了克隆算子的空间搜索能力。显然，如果可以保证其变异后个体的多样性和遍历性，就意味着通过变异搜索空间的算法拥有更强的搜索能力，在实际的工程应用中很难保证这一点。而利用混沌运动的这些性质可以进行具有遍历性的优化搜索。因此可以考虑将混沌搜索的特点引入克隆选择算法中，以提升其性能。

考虑到克隆选择算法和混沌优化算法各自的空间搜索优势，而且混沌序列可以用于模拟免疫细胞的增殖方式，在结合混沌优化算法和克隆选择算法各自特点的基础上，提出三种混沌免疫克隆选择算法(chaos immune clonal selection algorithm，CICSA)。

1.混沌映射和混沌扰动方式的确定

与其他产生混沌变量的混沌迭代方程比较，Logistic方程使用方便、计算量小。因此采用式(4-17)来产生混沌序列：

式中，z为混沌变量，0＜zk＜1；k为混沌迭代数，k＝1，2，…；η为控制参数，当η＝4时系统完全处于混沌状态，其混沌空间为(0，1)。

对于随机扰动的确定，令(www.xing528.com)

式中，β∗为最优混沌向量，是当前最优值(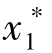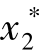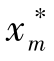，，…，)映射到[0，1]区间后形成的向量；βk为迭代k次后的混沌向量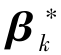；为引入了随机扰动后的混沌向量；另外0＜α＜1，α可以自适应变化。在搜索开始时希望变量变化较大，α值较大，随着搜索的进行当变量接近最优值时，α也应逐渐减小。算法按照下式确定：

式中，p为整数，可以根据目标函数而定；k为算法迭代次数。

因此在原有算法中引入自适应混沌变异，利用个体质量、迭代次数和抗体的分布情况自适应控制变异尺度，能够充分利用先验知识指导变异，避免搜索的盲目性，比非均匀变异具有较高的精度和效率。

2.混沌搜索算法和克隆选择算法的结合

克隆选择算法与混沌搜索算法有三种结合方式：可以将混沌优化作用于总抗体群中用于克隆变异操作的那部分，也可作用于记忆抗体中的部分抗体，更可以用于总抗体中部分抗体。这三种方式可见如图4-5所示的混沌搜索算法和克隆选择算法的结合。

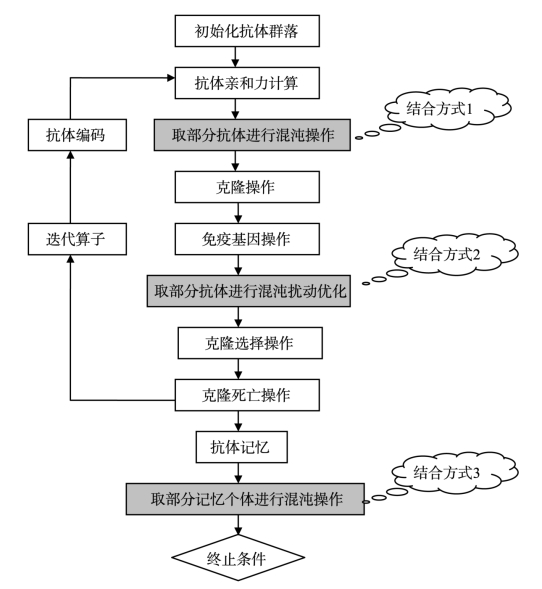
图4-5　混沌搜索算法和克隆选择算法的结合