土地用途聚类问题及其多目标优化解决方案

土地用途分区在本质上是一个组合优化问题，优化是指在可接纳的约束条件下发现最佳的可接受解的过程。最优化问题(optimization problem)一般是指按照给定的标准在某些约束条件下选取最优的解集，即在资源给定的情况下寻找最优的目标，或在目标确定下使用最少的资源。在土地用途区的划分过程中，基本的问题是将待分划的区域样本通过选定的样本特征来进行表达，样本是分布在特征空间上的离散的集合。空间聚类是一个解决组合优化问题的典型方法。因此在土地用途分区中可使用多目标优化的聚类方法来解决。这需要给出或者界定不同地区的特征和模式，根据这些特征和模式对研究区内的所有图斑进行聚类。通常，这样聚类需要计算样本和模式之间的最佳匹配程度，找到最佳匹配，才能进行合理的分区和规划。从而，这一规划的分类问题可以通过引入优化理论和优化方法来解决。但是土地用途分区问题在优化问题领域有其独特的复杂性和难点，具体体现为以下几个方面：

①其优化目标和约束条件中存在非线性项，具有高维和大量局部最优解；

②由多维特征变量描述的目标函数；

③在约束条件和目标函数中参数不确定。

土地用途分区这个优化问题就包含了非线性、动态、组合、多目标和不确定性等多种特性，是一个具有高度复杂性的优化求解问题。在这种复杂性和不确定性下，传统的方法很难获得最优解，选择聚类的思路和方法来处理这一求解问题。基于这一观点，土地用途区划分问题可以表述为以下的多目标优化聚类问题。

1.基于多目标优化聚类的土地用途分区问题的形式化描述

假设X＝{x1，x2，…，xn}表示一组具有n个样本的数据集，其中xi＝(xi1，xi2，…，xim)T表示第i个样本的m个特征值。那么对X进行聚类的目的就是要找到一个最优划分，将X中样本分为k类，其中k是一个正整数。土地用途分区的聚类问题形式化描述如下：

式中，X＝(n，m)为图斑，n是图斑个数，m是维数，在土地用途分区中可以看作图斑的属性；S是相似度量算法；C是约束条件；T是终止条件；A是选择的智能算法；R是土地用途分区的聚类结果。

对于按一定方式给定的n个样本，样本集可能的划分数目常常是无法估算的，通过逐个研究每一个划分来找到最好划分是不切实际的。因此，通常的解决办法是选择聚类准则来指导搜索划分，希望找到一组聚类中心，通过样本点和聚类中心的距离判别样本点的归属，并且达到类内差异最小，同时满足类间差异最大。可以采用定义一个目标函数作为聚类准则的方法来解决这一问题，该目标函数称为知识。因此基于多目标优化的土地用途分区模型可以表述为：在约束知识指导下的土地用途分区聚类问题。需要解决土地用途分区的多目标优化聚类问题。

2.土地用途分区多目标优化聚类面临的问题(www.xing528.com)

①土地用途分区常常要处理海量高维特征数据集，这些数据通常是由十几种甚至几十种特征(时间、比值、二值化、序数、名词等)来描述的。所以对土地用途分区中的对象——图斑进行聚类是一个具有挑战性的课题。

②地类图斑的属性往往既有数值型的也有类属型的，具有混合属性特征。这就要求数据挖掘算法能够处理这种同时具有各种不同属性特征类型的数据集。由于类属性是无序的，所以将类属型特征转化为数值特征的传统方法无法得到满意的结果。现有大多数聚类分析算法或者能处理这种混合特征型数据，但不适用于大规模数据集，或者能有效处理大规模数据集，却仅限于数值型特征，从而限制了其在数据挖掘中的应用。为此，希望能设计出一种既能处理混合特征型数据又能发展成为数据库中知识发现的有利工具。

③聚类分析的主要目的是将数据分成一系列相互区分的组，以利于从中发现数据集的整个空间分布规律和典型模式(王生生，2005)。然而对于土地用途分区问题，简单地按照地类图斑的空间距离进行相似测度是不现实的，这也是土地用途分区的难点之一。

传统的聚类算法没有充分考虑到空间数据海量和复杂性的特征，因此当面对土地用途分区这一新的挖掘任务时，就会导致原有算法效率低下甚至失效而不能应用。因此，一方面需要改进传统的聚类算法来处理复杂性问题和海量数据，另一方面则需要探索并结合其他领域的研究成果，并提出新的可适用于土地用途分区聚类的高效算法。

3.空间聚类分析方法

在数据挖掘领域，聚类是一个用于发现隐藏在空间数据库中的知识的有效方式(Yang Jianfeng，2008)。空间聚类是在海量空间数据集中通过度量空间实体间的相似程度，来逐步合并类簇使类间差异最大而类内差异达到最小的过程(J.Han＆M.Kamber，2000)。本质上，数据聚类是一种数据驱动的非监督学习方法。目前已有的空间聚类算法如图4-1表示，还有一些用数据场、粗集、模糊集和小波理论等理论的研究报道，这些算法都是在传统算法的基础上集成了多种聚类方法的思想，因此有时很难将某个指定算法具体划分到某种聚类方法中。这些方法都具有各自的特点：有些以方法简单、容易实现并且执行效率高为优点；有些对任意形状、大小的类识别能力强；有些能很好地过滤噪声数据。但这些方法都有各自的局限性，如密度类算法采用全局参数，对密度变化较大的类不能得到真正的自然聚类结果；网格类算法效率虽然很高，但是聚类的精确度又不能让用户满意。另外，很多聚类方法对输入参数十分敏感，而且参数很难确定，如划分方法中的k。

近年来，国内外有关空间聚类算法的研究主要有以下几个方向：第一，对传统经典模型的扩展；第二，融合多种聚类方法的思想；第三，提出了新的空间聚类算法。为了解决海量、高维数据处理的问题(B.M.H.Romeny，1997)，将其他学科的最新研究成果如图论、模糊数学(Eschrich S.et al.，2003)、人工智能(如遗传算法(U.Mali，2000))引入空间聚类研究中。关于空间聚类最新的研究成果是提出了许多基于遗传算法的聚类算法，但收敛速度较慢、容易出现早熟一直是不能解决大规模应用的瓶颈问题。

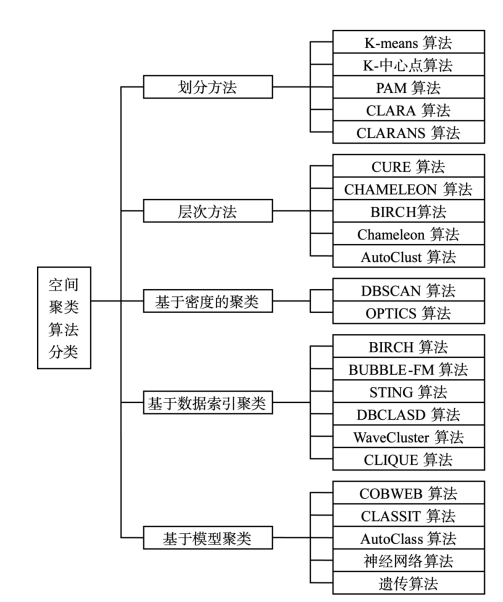
图4-1　传统的空间聚类分析方法

基于以上研究中存在的问题，面对空间数据的海量、高维等复杂性特征，本书提出适合的、高效的聚类分析算法，将克隆选择算法引入空间数据聚类中，并根据土地用途分区的具体问题给予改进，提出新的空间聚类挖掘模型，用于解决土地用途分区问题。