在3.3.1和3.3.2的模糊概念格的构造算法中已经考虑了Hasse图的绘制问题,在建格过程中同时确定各节点的父节点的集合和子节点的集合。因此Hasse图绘制的过程中需要解决两个问题:一是如何确定节点的坐标,这是Hasse图绘制的关键问题,二是如何来绘制,当第一个问题解决后,就可以在父子格节点之间绘制一条线段(O.Kwon,2009)。
1.模糊概念格节点坐标确定方法
对于已经建设的模糊概念格如果要绘制Hasse图就必须确定格节点的层号、y坐标的x坐标。根据这一原则,下文将说明模糊概念格节点的数据结构。在建格时就需要考虑Hasse图的绘制,一般应采用一定的数据结构,数据结构中应该说明以下方面的内容节点的标识码、节点的层数、节点的内涵(项目集)、外延的基数(具有共同的内涵的对象的数目)、子节点的标识码、父节点的标识码、节点的x坐标、节点的y坐标以及其他需要的内容。
采取这样的数据结构,根据预先确定的层号和层间距离,可以直接得到某节点的y坐标。如何确定x坐标相对比较困难。同一层节点的序号用nNum表示(即同一层的第nNum个节点),X方向的相邻节点之间的间隔用nDeltaxX表示。x坐标的确定方法如下:假设用Xcenter表示绘图区域X方向的中点的X值,为了保证Hasse图的美观应将同层中首先生成的节点绘制在绘图区域的中心,其余的按一定间隔平均分布在中心的两侧,该过程可以表达为:
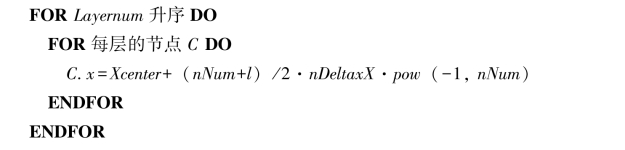
这一算法保证了在X方向上同一层的所有节点等距离均匀分布在绘图区域的中点的两边。
2.基于辞典树模糊概念格节点坐标确定算法
在提出的基于辞典树模糊概念格节点坐标确定算法中,自动绘制Hasse图的基本思想是将模糊概念格的节点按照内涵集的大小分层存放,然后根据层号确定任一节点的y坐标。这需要一个能够描述这些信息的结构,首先定义一个概念格节点的链表,对于每一个节点,应该能够在这个结构中自动记录以下信息:节点的层数、外延的基数、节点进入概念格的次序、子节点集合、父节点集合、节点的x坐标、节点的y坐标、指示是否为频繁节点以及节点的内涵等相关内容。x坐标与“模糊概念格节点坐标确定方法”中的计算方法相同。(https://www.xing528.com)
3.绘制Hasse图
在进行概念格的构建的同时,需要进行节点坐标的设置。采用动态的方式设定层与层之间的距离以及每一层中各节点之间的距离。设定xDim,yDim为绘制Hasse图的最大x和y范围,则y方向上的距离为dy=yDim/(LayerNum+1),LayerNum为最大层数。每一层的y坐标为(LayerNum+1)×dy,layer为各节点所位于的层数。对于x方向的距离dy=(xDim-xStart)/(VexNum+2),x方向上的起始点坐标为xStart。可以让同一层节点按照加入的先后顺序左右分别布置在中心线的两边,因此可以采用下式进行计算,x=xstart+(-l)(count+1)×(count+l)/2×dx,其中count为同一层节点的加入顺序。
在建格完成并确定了每个节点的X,Y坐标后,对所有节点进行排序,并根据概念格中记录的父子关系,分别在子节点与其父节点之间画线,即可得模糊概念格的Hasse图。算法如下:
算法3-3:Hasse图绘制。

使用本研究中提出的模糊概念格渐进式构造算法对例2的形式背景进行处理,得到如图3-3所示的模糊概念格。从图中可以看出,虽然例2和例1的对象和属性个数相当,但是生成的概念格节点数量差别很大,因此基于索引树的模糊概念格生成算法是有效的。
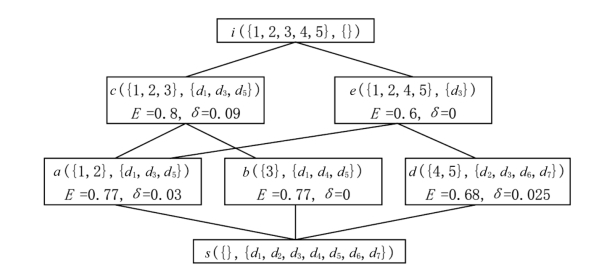
图3-3 由例2的模糊概念格绘制的Hasse图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




