探究土地利用关联规则挖掘的模糊概念格方法

在认识和改造世界的过程中，人类把所感觉事物和现象的共同特点抽象并加以概括，形成了概念。基于哲学中认为概念是由内涵和外延组成的思想单元这一思想，德国的Rodolf Wille教授于1982年首先提出了形式概念分析的理论。这一理论是基于概念和概念层次的数学化表达的应用数学的一个分支。关于概念格的理论，已有众多的学者进行了研究，在此不再赘述。为了较好地处理土地用途分区的知识获取问题，主要对采用模糊概念格对土地利用关联规则进行挖掘的问题进行研究。

1.模糊概念格

随着计算机的发展和对地观测技术的进步，越来越多的数据被保存在土地利用时空数据库中，信息量的俱增，与此同时出现了越来越多的模糊信息导致数据难以利用。美国人扎德最早提出了模糊集理论并应用于模糊控制中，其后众多学者不断发展这一理论。目前该理论是解决模糊问题的重要方法。基于此本研究中拟使用模糊概念格进行空间关联规则挖掘，并对模糊概念格进行研究，以利于土地数据库的空间关联规则挖掘。

模糊形式背景K＝(U，A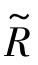，)，其中U为对象集，对象o∈U；A为模糊属性标识集，属性d∈A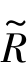；是映射，满足式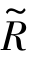：U×A→[0，1]，或写成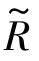(o，d)＝m，0≤m≤1。隶属度函数可以是一般函数(Hongliang Lai，2009)。

在模糊形式背景K中，O∈U，D∈A，对于D中的每个属性d选取阈值φdj(0≤φdj≤1)在O和D间可定义两个映射f和g，如下式表示：

式中，f和g称为U的幂集和A的幂集之间的Galois连接。

如果二元组C＝(O，D)(O⊆U，D⊆A)满足：O＝g(D)，D＝f(O)，则称为模糊背景K的一个模糊概念，O和D分别是模糊概念C的外延和内涵。模糊形式背景K的所有模糊概念的集合记为CS(K)。CS(K)上的结构是通过泛化、例化关系产生的，其定义为：如果模糊概念C1＝(O1，D1)和C2＝(O2，D2)的两个对象集O1、O2满足O1⊆O2，则满足(O1，D1)≤(O2，D2)。通过此关系得到的有序集CS(K)＝(CS(K)，≤)称作模糊形式背景K的模糊概念格。

模糊参数E：对于对象集合O和属性集合D＝f(O)，d∈D，参数E为：

当需要指明(O，D)时，分别写为Ed(O，D)和E(O，D)。

模糊参数δ：对于对象集合O和属性集合D＝f(O)，d∈D，参数δ定义如下：(www.xing528.com)

当需要指明(O，D)时，分别写为δd(O，D)和δ(O，D)。

对每个模糊概念C＝(O，D)(O⊆U，D⊆A)，应用模糊背景的信息计算模糊参数E值和δ值，采用E和δ，可以在从模糊概念格提取关联规则时避免生成冗余节点，进而避免生成效果欠佳的规则。

E是C中所有对象的平均隶属度。δ是所有δd(C)的均值，其中δd(C)是C中所有对象的隶属度值相对基于属性d的隶属度均值的偏离程度，δ反映了C中对象的隶属度值相对平均隶属度的偏离程度。

在模糊概念格的构造算法中，为了能够用渐进式方法计算参数E和δ，引进中间变量kd、hd：

由中间变量kd、hd可以计算E、δ：

2.概念格的应用领域

作为数据分析和知识处理的形式化工具，经过近二十年的发展，概念格(形式概念分析理论中的一种核心数据结构)已经在众多的领域取得了广泛而成功的应用。在软件工程领域，形式概念分析为再工程、软件重用、面向对象程序设计等领域中某些问题的解决提供了理论支持，并已经取得了一系列的应用成果。在数据挖掘领域，由于形式概念分析以概念格的形式使数据有机地组织起来，因此可以从关系数据中构造出来。概念格节点体现了概念内涵和外延的统一，因此非常适合于用来发现规则型知识，如蕴含规则、关联规则、分类规则等。除了在软件工程和数据挖掘领域获得的研究成果外，概念格还被成功地应用于信息检索、知识库组织等诸多领域(Lei Yinbin et al.，2009)。

综上所述，每个概念格节点都是一个形式概念，由外延和内涵两个部分组成。在规则的挖掘过程中，用内涵集之间的关系来描述规则，它体现了相应外延集之间的包含(或近似包含)关系。由于概念格节点反映了概念内涵和外延的统一，节点间关系体现了概念之间的泛化和例化关系，因此非常适合作为规则提取的基础性数据结构。在既有研究的基础上提出模糊概念格和其构造算法，并用于土地利用分区中的关联规则挖掘，具体内容在第3章详细介绍。