工业部门生产函数的多重共线性优化分析结果

在上一节讨论的数据基础上，本节估计中国工业部门的生产函数，比较该部门中私营和国有两类企业的实物资本边际产出以及投资效果。

首先，对生产函数［式（6-1）］两边取对数，得回归等式：

式中，截距项a0对应式（6-1）中的全要素生产率；a1，a2和a3分别表示国有企业实物资本存量、私营企业实物资本存量与人力资本存量Ht的产出弹性；ut是随机误差项。

式（6-17）的回归分析结果（表6-15）显示。

（1）根据一元回归的结果，私营企业实物资本、国有企业实物资本与人力资本Ht的系数估计值均显著，各要素的产出效果明显。

（2）私营与国有企业实物资本存量可以共同解释99.60%的部门产出，较之人力资本，实物资本积累的产出效果更为明显（这也部分解释了中国工业部门增长对实物资本积累的依赖性）。

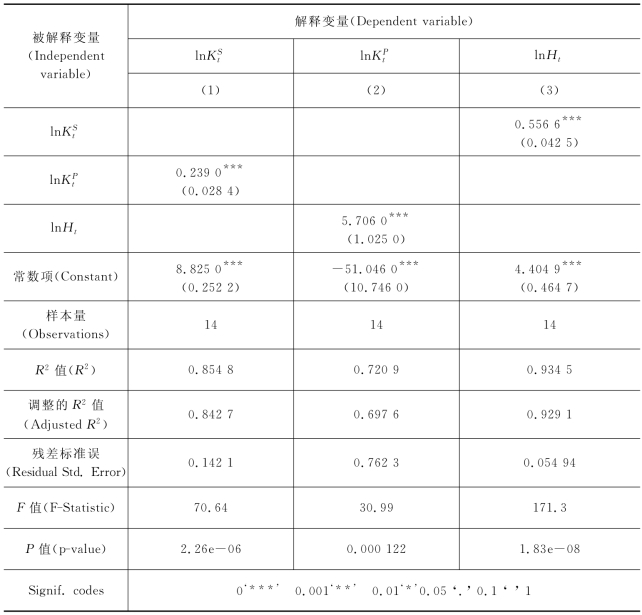
（3）用实物资本与人力资本共同解释工业部门产出，Ht的产出弹性不显著（t值为1.76），原因在于和Ht之间存在多重共线性（表6-16）。

表6-15　回归：工业部门基准生产函数

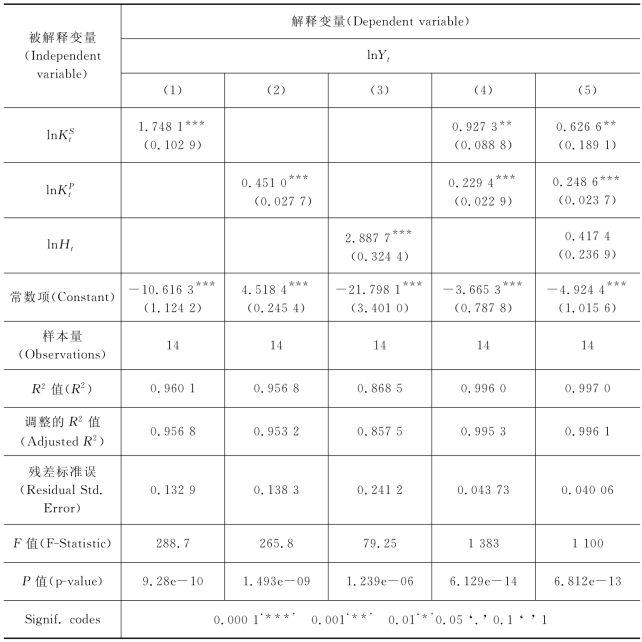
表6-16　回归：投入要素共线性检验

为了消除多重共线性，设工业部门生产规模报酬不变，即α+βS+βP=1，对式（6-1）两边同时除以Ht^[9]并取对数。变形后的回归式为(www.xing528.com)

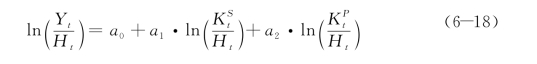
式中，a1，a2分别表示的产出弹性，人力资本的产出弹性α可间接求得，即α=1-a1-a2。式（6-18）回归结果见表4-17列（1）。

表6-17　回归：调整后的工业部门生产函数

由表6-17列（1）回归结果可知，消除多重共线性后各解释变量的系数均显著，且回归等式的整体拟合优度达99.88%。但是，实物资本产出弹性之和大于1（a1+a2=1.125 3＞1），与之前的模型假定不符。因此，再设定中国工业部门生产规模报酬递增，即α+βS+βP＞1，并将回归等式改写为

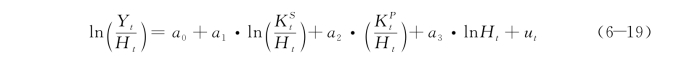
式中，a1，a2分别表示的产出弹性；人力资本产出弹性α=1+a1+a2-a3。式（6-19）的回归结果如表6-17列（2）所示。

与式（6-18）回归结果相比，式（6-19）的拟合优度提高至99.40%，并且F值和p值均理想，残差标准差较低，各个解释变量的系数及常数项均显著，能更贴切地描述工业部门生产函数。据此，中国工业部门的生产函数可近似表示为

通过以上分析（表6-15，表6-17及式（6-20）），可知：

（1）中国工业部门具有规模报酬递增的特征（要素产出弹性和为1.29），这说明该部门尚有进一步扩张的空间；

（2）实物资本产出弹性的显著性水平高于人力资本，前者对工业部门的产出影响更明显，这说明投资仍是工业经济扩张的重要途径；

（3）国有企业实物资本的产出弹性高于私营企业（βS=0.63＞βP=0.25），这意味着中国工业部门中，国有企业采用资本密集度更高的生产方式，而私营企业资本密集度偏低或与其融资约束较之国有企业更严格有关。