柑橘市场价格预测模型及应用分析

（1）数据来源。以2003—2016年的《中国农产品价格调查年鉴》、中国经济与社会发展统计数据库为来源，选取2002年1月至2015年6月橙子月度集贸市场价格数据进行实证分析，其中前13年156个数据作为网络训练的样本数据，2015年1～6月的数据作为对网络预测数据的检验。

（2）时间序列预测模型的选择与预测结果。第一，市场价格序列的检验。首先采用ADE检验对橙子月度集贸市场价格时间序列的平稳性进行检验，由检验结果（见表6-14）可以看出橙子集贸市场价格时间序列存在单位根，为不平稳时间序列，而该序列经过一阶差分后已经消除了单位根，为平稳时间序列，因此可以判断橙子市场价格序列为一阶单整序列。平稳性检验结果表明，适用于非平稳序列的ARIMA、ARCH模型可以用于以上橙子市场价格的短期预测。

表6-14　橙子市场价格时间序列平稳性检验结果
Table 6-14　The stability test results of orange market price time series

其次进行趋势性、季节性检验。将橙子月度集贸市场价格做时序图，如图6-9所示，橙子市场价格序列存在着明显的趋势性和季节性。为进一步验证其趋势性，通过构建含有时间趋势的线性回归模型，运用最小二乘法进行估计，得到的估计与检验结果（见表6-15）显示：回归模型中时间趋势项在1%的显著性水平下显著，表明橙子价格序列呈现明显的趋势性，因此可以选择适用于有趋势性的时间序列模型来进行其市场价格的短期预测，如二次指数平滑、Holt—Winters指数平滑模型等。为进一步验证其季节性，通过构建含有季度虚拟变量的线性回归模型，运用最小二乘法进行估计，得到的估计与检验结果（见表6-16）显示：橙子建立的回归模型中季节虚拟变量在1%的显著性水平下显著，表明橙子价格序列呈现明显的季节性，可以选择含有季节变动的如Holt—Winters指数平滑模型、Census X12季节分解模型、SARIMA模型进行市场价格的短期预测。

图6-9　橙子集贸市场价格时间序列图
Eig.6-9　Orange market price time sequence diagram

表6-15　橙子市场价格趋势性检验结果
Table 6-15　The trend test results of orange market price

表6-16　橙子市场价格季节性检验结果
Table 6-16　The seasonal test results of orange market price

最后进行条件异方差检验。对橙子月度集贸市场价格使用条件异方差拉格朗日（ARCH-LM）检验，结果表明其价格序列不存在条件异方差，可使用ARIMA或SARIMA模型进行市场价格的短期预测，具体检验结果见表6-17。

表6-17　橙子市场价格的ARCH-LM检验结果
Table 6-17　The ARCH-LM test results of orange market price

第二，时间序列预测模型的选择与预测。综合以上检验结果可以确定，在样本期内，中国橙子月度集贸市场价格时间序列均具有非平稳性、趋势性、季节性和无条件异方差性。根据上述特征，结合不同时间序列模型的适用范围和条件，使用Holt—Winters季节性指数平滑模型、Census X12的季节分解模型和SARIMA模型分别进行橙子市场价格序列的拟合和短期预测，其中SARIMA模型均通过原始价格序列、差分序列和季节差分序列的自相关图识别模型阶数并比较不同阶数模型的拟合效果，选择拟合优度高，SC值和AIC值小的模型。具体模型的选择结果见表6-18。

表6-18　橙子市场价格预测模型选择
Table 6-18　The selection of orange market price forecasting model

根据以上单项时间序列预测模型对橙子月度集贸市场价格分别进行模型拟合，并对2015年1～6月的市场价格进行预测，通过预测值和实际值之间平均绝对百分比误差的大小比较，拟合及预测结果显示：对Holt—winters季节乘法模型预测精度较高，Census X12的季节分解模型预测精度相对最低。具体各模型的预测误差见表6-19。(www.xing528.com)

表6-19　橙子市场价格时间序列预测模型预测误差
Table 6-19　The prediction error of orange market price time forecasting model

（3）智能预测模型的选择与预测结果。第一，BP神经网络预测。利用MATLAB R2012b软件实现该BP神经网络的构建，使用2002年1月至2014年12月的数据进行预警模型训练，用2015年1～6月的数据进行模型测试。网络训练函数采用Trainlm函数，传递函数为Tansig函数，设定最大训练次数为2000次，训练目标最小误差为0.01，Levenberg-Marquart优化算法的调整参数mu=0.1，橙子月度集贸市场价格经过10次训练后，误差达到目标值，结果满足要求，如图6-10所示。

图6-10　橙子市场价格BP神经网络预测模型训练过程
Eig.6-10　The training process of BP neural network of orange market price forecasting model

第二，灰色系统模型预测。根据灰色系统模型GM（1，1）及橙子月度集贸市场价格数据，分别计算出其模型的参数β1、β2的估计值，并将所建立的灰色预测模型分别进行了残差检验、关联度检验和后验差检验，由检验结果（见表6-20）可知，橙市场价格的关联度是0.76，大于0.6的最低关联度标准，精度等级为3；后验差比值为0.15，小于0.35，精度等级为1，这说明灰色系统模型适合进行橙子市场价格的短期预测。

表6-20　橙子市场价格灰色预测模型参数估计和检验结果
Table 6-20　The parameter estimation and test results of GM（1，1）of orange market price

注：关联度标准为1级-（0.9，1）；2级-（0.8，0.9）；3级-（0.7，0.8）；4级-（0.6，0.7）；后验差比值标准1级-0.35；2级-0.50；3级-0.65；4级-0.80

根据BP神经模型和灰色系统模型GM（1，1）对橙子月度集贸市场价格分别进行模型拟合，并对2015年1～6月的价格进行预测，通过预测值和实际值之间平均绝对百分比误差的比较，拟合及预测结果显示：BP神经网络模型预测误差较小，灰色系统模型GM（1，1）预测误差相对较大。具体各模型预测误差见表6-21。

表6-21　橙子市场价格智能预测模型预测误差
Table 6-21　The prediction error of orange market price intelligent forecasting model

（4）构建组合预测模型。由于组合预测模型中的单项预测模型数量达到一定量时，继续增加模型反而可能会降低组合预测精度，因此首先对橙子月度集贸市场价格组合预测模型中的单项预测模型进行筛选。具体操作方法是从5种单项预测模型中选择3种预测精度相对较高的模型进行组合；再以入选的单项预测模型预测结果误差小则权重高为基本原则，选取方差倒数法来计算权重，构建市场价格短期预测的组合预测模型；最后对组合预测模型的预测模拟结果进行检验，计算其绝对百分比误差，与单项时间序列模型的预测误差进行比较，以确定最终的拟合效果。由拟合结果可知：橙子月度集贸市场价格的短期预测，选取了Holt—Winters季节性指数平滑模型、Census X12的季节分解模型和SARIMA模型进行加权组合，最终的预测误差为3.04%，小于Holt—Winters季节性指数平滑模型、Census X12的季节分解模型和SARIMA模型的预测误差。具体拟合效果见表6-22。

表6-22　橙子市场价格组合预测模型权重及预测误差
Table 6-22　The weight of combination forecasting model and prediction error of orange market price

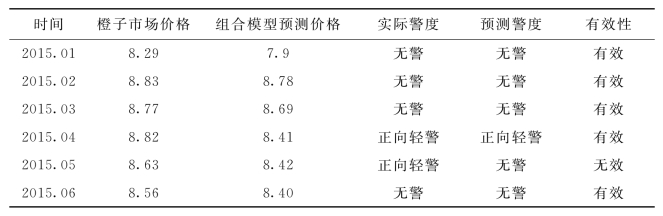
根据组合预测模型对2015年1～6月的橙子市场价格的预测值，参考风险价值法（VaR）设置的橙子市场月度价格的警限区间分别为：负向重警（-∞，-6.59%），负向轻警（-6.59%，-3.0%），无警（-3.0%，3.8%），正向轻警（3.8%，8.74%），正向重警（8.74%，∞），可以得知6个月中除4月份出现正向轻警外，其余月份均为无警，这与实际警度基本一致，有效性达到83.3%，见表6-23。

表6-23　橙子市场价格组合预测值与预警警度及有效性
Table 6-23　The combination prediction and warning degree of orange market price