收益共享契约的博弈模型及其对生鲜电商平台和零售商的影响

从上一节的分析中，我们发现在批发价契约中，双方的利润和保鲜投入水平会随着双方主体地位的差异而发生变化。博弈中的主导方获得的利润较多，但整体的新鲜度水平并没有发生变化。因此，为了使供应链新鲜度和双方的利润水平都能得到提升，本文将引入收益共享契约进行协调。双方从整体利益最大化的角度确定销售价格，同时零售商将销售总收入中的一定比例返还给生鲜电商平台。假设这部分比例为φ，那么零售商从销售总收入中获得的比例为1-φ。由于篇幅限制，本文只讨论生鲜电商平台领先的收益共享契约模式，那么此时双方的目标函数为

命题5.7：在收益共享契约下的博弈模型中，销售价格和以及生鲜电商平台和零售商的保鲜投入Ic和Fc分别为 （其中上标c表示收益共享契约模式）：

证明：利用逆向归纳法求解，根据最优控制理论，可以假设连续有界的微分利润函数Vi（G）对于任意的G≥0，存在HJB方程，即

首先对式 （5.47）求p1，p2的一阶偏导，并分别令其等于零，则可得到

并求其海塞矩阵

由于且4λ2-4＜0，因此目标函数存在最大值。求解式（5.48）中的方程组，可以得到线上线下的销售价格如命题5.7所示。

分别对式 （5.46）求I的一阶偏导并对式 （5.47）求F的一阶偏导，并令其等于零，得到

将命题5.7中和以及和代入式 （5.46）和式（5.47）中，可得

由式 （5.49）和式 （5.50）的结构得到，关于G的线性最优价值函数是HJB方程的解。令其中为待定系数，且满足结合式 （5.49）和式 （5.50），得到最优价值函数的参数分别为：

把代入式（5.51）和式（5.52）中且结合和Fc可得生鲜电商平台和零售商的最优保鲜投入如命题5.7所示。同时，生鲜电商平台和零售商的长期利润函数可表示为：

命题5.8：在收益共享契约下的博弈模型中，供应链中生鲜农产品质量水平的最优轨迹Gc（t）为

其中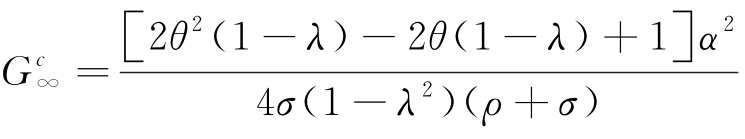，为收益共享契约中新鲜度水平的稳定值。

推论5.12：相对于批发价格契约，在收益共享契约下生鲜农产品的线上线下销售价格都有所减少。

证明：生鲜农产品在两种契约下线上线下的销售价格差分别为：

根据式 （5.54）和式 （5.55）可得由此可见，在收益共享契约下，线上线下的销售价格相对于批发价格契约下要有所偏低。(www.xing528.com)

推论5.13：当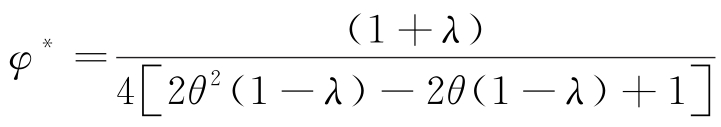时，收益共享契约能确保生鲜电商平台和零售商的保鲜投入同时达到批发价契约中的最优水平，从而促进供应链新鲜度水平的提升。

证明：根据推论5.10可知，在生鲜电商平台为主导的批发价契约中，生鲜电商平台保鲜投入较大。因此，只要当Ic=Iss时，收益共享契约就能使生鲜电商平台的保鲜投入达到批发价契约中的最优水平，即

得到

同理可证，当时，Fc=Frs，即零售商的保鲜投入达到批发价契约中的最优水平。由可知，当

时，收益共享契约能确保生鲜电商平台和零售商的保鲜投入同时达到批发价契约中的最优水平，而此时供应链新鲜度水平的变化为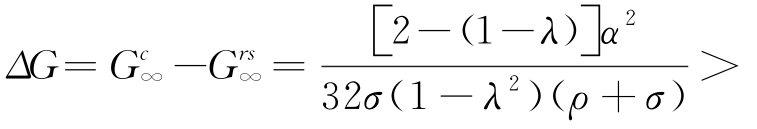0，由此可见，供应链的新鲜度水平得到了改善，推论5.13得证。

推论5.14：当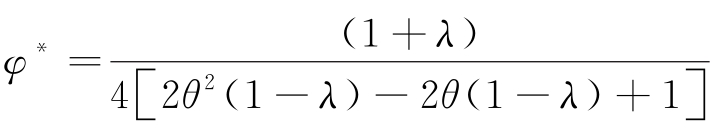时，双方利润均优于批发价契约中的最优利润，供应链实现了帕累托改善。

证明：将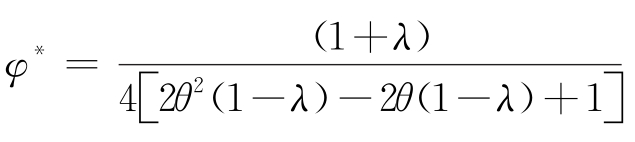代入式 （5.39），得到收益共享契约下双方的利润函数，并将其与批发价契约中双方的最优利润水平进行对比，可得

由式 （5.56）和式 （5.57）可知和因此双方的利润水平均优于批发价契约中双方的最优利润水平，从而实现了供应链双方的帕累托改善，因此推论5.14得证。

推论5.15：在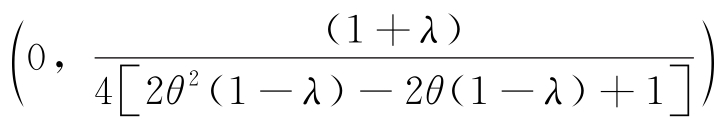区间中，存在φ1使得生鲜电商平台在收益共享契约和生鲜电商平台为主导的批发价契约两种情形下的利润相等；在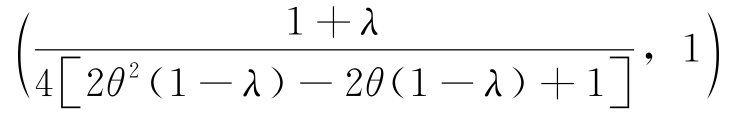区间中，存在φ2使得零售商在收益共享契约下与零售商为主导的批发价契约下的利润相等；当φ∈（φ1，φ2）时，生鲜电商平台与零售商的利润均优于批发价契约下的最优利润，供应链实现了帕累托改进。

证明：由推论5.10可知，生鲜电商平台在生鲜电商平台为主导的批发价契约中的相对利润较大，因此假设那么f（φ）为关于φ的一元二次函数，通过计算可以得到

根据零点定理和罗尔中值定理，可以得到在

的区间中，存在唯一的φ1，使得JcE=JssE。同理可得，在

区间中，存在φ2使得JcR=JrsR。因此当φ∈（φ1，φ2）时，收益共享契约使得生鲜电商平台和零售商的利润都得到了改善。