批发价契约下的生鲜电商博弈模型及线上线下价格差的相关性

在批发价契约中，生鲜电商平台以批发价ω向零售商销售产品，零售商决定线上线下的销售价格p1和p2，此时双方的目标函数为：

由于生鲜电商平台和零售商在合作中的地位存在差异，因此合作过程中的主导方也会随之变化。如果生鲜电商平台的实力更为雄厚，那么其将拥有优先定价的权力，现实中较为成熟的生鲜电商平台如京东、苏宁等，其在与线下便利店合作时，他们将拥有优先定价权，此时双方的博弈即为生鲜电商平台主导的Stackelberg博弈情形。而当零售商的议价能力更强，如线下大型实体生鲜超市如沃尔玛、永辉超市等，其在与生鲜电商平台合作时，线下实体超市的议价能力更强，那么此时双方的博弈即为零售商主导的Stackelberg博弈情形。本文将分别考虑以上两种博弈情形，比较双方在定价，保鲜投入和利润等方面的差异。

5.2.2.1 生鲜电商平台主导的Stackelberg博弈模型

在生鲜电商平台主导的Stackelberg博弈模型中，其博弈顺序为：第一阶段，生鲜电商平台预见到零售商的反应制定最优的批发价格ω，确保自身的利润最大化；第二阶段，零售商根据生鲜电商平台给定的批发价制定生鲜农产品线上和线下的销售价格p1和p2，最大化自身的利益。

命题5.3：在生鲜电商平台主导的Stackelberg博弈模型中，批发价格ωss，销售价格和以及生鲜电商平台和零售商的保鲜投入Iss和Fss的数学表达式分别为（其中上标ss表示以生鲜电商平台主导的Stackelberg博弈模型）：

证明：利用逆向归纳法求解。根据最优控制理论，可以假设连续有界的微分利润函数Vi（G）对于任意的G≥0，存在HJB方程，即

首先对式 （5.20）求p1，p2的一阶偏导，并分别令其等于零，则可得到

求其海塞矩阵

由于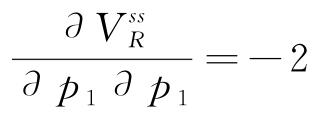且4λ2-4＜0，因此式 （5.20）存在最大值。求解式 （5.21）中的方程组，可以得到

然后，对式 （5.20）求F的一阶偏导，并令其等于零，得到

将式 （5.22）代入式 （5.19），对其求ω和I的一阶偏导，并令其等于零，得到

将代入式 （5.22）中，即可得到线上线下的最优价格如命题5.3中所示。

将命题5.3中ωss，和以及和代入式 （5.19）和式 （5.20）中，可得

由式 （5.23）和式 （5.24）的结构得到，关于G的线性最优价值函数是HJB方程的解，令其中为待定系数，且满足结合式 （5.23）和式 （5.24），得到最优价值函数的参数分别为

把代入式 （5.23）和式 （5.24）中，并结合和可得生鲜电商平台和零售商的最优保鲜投入如命题5.3所示。同时，生鲜电商平台和零售商的长期利润函数可简化为：

命题5.4：在生鲜电商平台主导的Stackelberg博弈模型中，供应链生鲜农产品的新鲜度水平的最优轨迹： 其中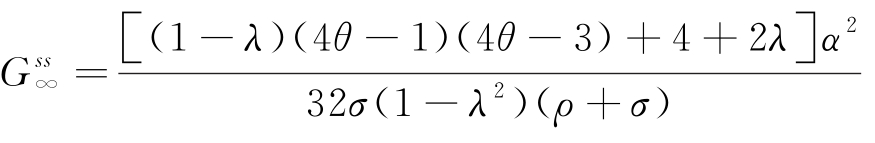，为生鲜电商平台主导的批发价契约中新鲜度水平的稳定值。

推论5.8：线上线下的价格差与θ正相关。当θ＞0.5时，线上线下的价格差与λ负相关，当θ＜0.5时，线上线下的价格差与λ正相关，当θ=0.5时，线上线下的价格差与λ没有相关关系。

证明：线上线下的销售价格差为

首先，对式 （5.28）求θ的一阶偏导，得到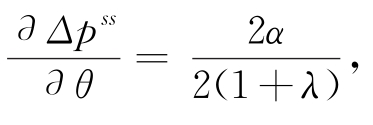可见线上线下的价格差与θ正相关，假如线下市场份额越大，相应价格越高，反之亦然。

其次，对式 （5.28）求λ的一阶偏导，得到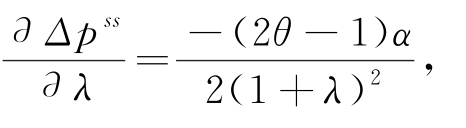可见当θ＞0.5时，线上线下的价格差与λ负相关；当θ＜0.5时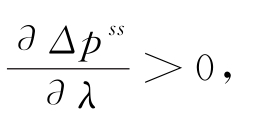，线上线下的价格差与λ正相关；当θ=0.5时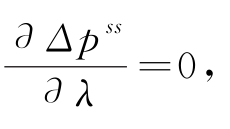，线上线下的价格差与λ没有相关关系，推论5.8得证。

推论5.8中的性质在现实中能够得到体现。目前生鲜电商平台虽然发展迅速，但仍未被消费者广泛接受。据商务部统计数据显示：2013年我国农产品的交易总额在4万亿元左右，其中80%是通过传统市场实现，线上需求所占到比例还较小，因此目前线上农产品的价格较线下普遍偏低。其次，生鲜农产品是一类非标准化产品，在生产、运输、销售过程中存在很多不确定性因素，而这些因素都会影响到消费者的体验，因此对于普通生鲜农产品，线上线下的交叉价格弹性较小，消费者更倾向于选择线下渠道进行亲身体验，而只有线上价格优惠足够大时才能吸引消费者购买。而为提高线上价格，目前大部分生鲜电商平台通过对生产源头建立一套严格的筛选机制，旨在提高线上生鲜农产品质量的稳定性，增大线上线下的交叉价格弹性。

5.2.2.2 零售商主导的Stackelberg博弈模型

在零售商主导的Stackelberg博弈模型中，其博弈顺序为：第一阶段——零售商预见到生鲜电商平台的反应，制定线上和线下的销售价格p1和p2，最大化自身的利润；第二阶段——生鲜电商平台根据零售商制定的销售价格确定最优的批发价格ω，确保自身的利润最大。

命题5.5：在零售商主导的Stackelberg博弈模型中，批发价格ωrs，销售价格和以及生鲜电商平台和零售商的保鲜投入Irs和Frs的数学表达式分别为 （其中上标rs表示以零售商主导的Stackelberg博弈模型）：(www.xing528.com)

证明：利用逆向归纳法求解，根据最优控制理论，可以假设连续有界的微分利润函数Vi（G）对于任意的G≥0，存在HJB方程，即

在以零售商主导的Stackelberg博弈模型中，我们假设零售商通过线上销售所获得的边际利润为Δ1=p1-ω，通过线下销售所获得的边际利润为Δ2=p2-ω，由此得到p1=Δ1+ω和p2=Δ2+ω，并将其代入式 （5.29）中，得到

对式 （5.31）求ω和I的一阶偏导，并令其等于零，得到

将Δ1=p1-ω和Δ2=p2-ω代入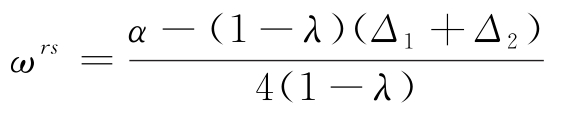中，得到代入式 （5.30），得到

对式 （5.32）求p1，p2的一阶偏导，并分别令其等于零，则可得到

求其海塞矩阵

由于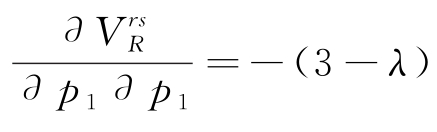且-8（1-λ2）＜0，因此目标函数存在最大值。求解式 （5.33）中的方程组，得到线上线下的最优价格如命题5.5所示，并将其代入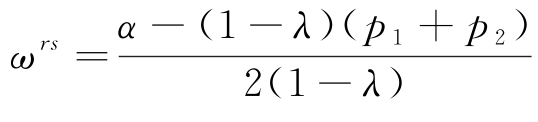中，得到生鲜电商平台的批发价为ωrs

同时，对式 （5.32）求F的一阶偏导，并分别令其等于零，得到

将命题5.5中ωrs，和以及和代入式 （5.29）和式 （5.30）中，可得

由式 （5.34）和式 （5.35）的结构得到关于G的线性最优价值函数是HJB方程的解，令其中为待定系数，且满足结合式（5.34）和式（5.35），得到最优价值函数的参数分别为

把代入式（5.34）和式（5.35）中，结合和可得生鲜电商平台和零售商的最优保鲜投入如命题5.5所示，同时，生鲜电商平台和零售商的长期利润函数可简化表示为：

命题5.6：在零售商主导的Stackelberg博弈模型中，供应链中生鲜农产品的新鲜度水平最优轨迹Grs（t）为

其中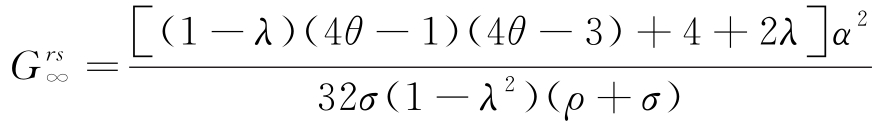，为零售商主导的批发价契约中新鲜度水平的稳定值。

推论5.9：在零售商主导的批发价契约中，批发价小于生鲜电商平台主导的批发价契约中的结果，即ωrs＜ωss。而零售商主导的批发价契约与生鲜电商平台主导的批发价契约中的线上线下销售价相等，即

证明：两种批发价契约中的批发价差为

因此ωrs＜ωss得证。根据命题5.3和命题5.5中线上线下销售价格的表达式，可知

因此两种批发价契约中的线上线下销售价相等，推论5.9得证。

推论5.10：与生鲜电商平台主导的批发价契约相比，零售商主导的批发价契约中生鲜电商平台所获得的长期利润水平相对减少，而零售商的长期利润水平相对增加，但供应链整体利润水平有所降低。

证明：根据命题5.3和命题5.5中的表达式，将两种批发价契约中生鲜电商平台和零售商的长期利润水平进行对比，得到

由式 （5.39）和式 （5.40），不难看出和，而供应链的整体利润变化由式 （5.41）可得ΔJs＜0，供应链的整体利润水平有所降低。而导致两种批发价契约模式中利润水平存在差异的原因在于，在线上线下销售价格一定的情形下，由于价格因素所导致的需求没有发生变化，批发价的降低会导致生鲜电商平台利润减少，而零售商利润增加，同时生鲜电商平台利润的减少量大于零售商利润的增加量，因此供应链整体的利润水平有所降低，推论5.10得证。

推论5.11：与生鲜电商平台主导的批发价契约相比，在零售商主导的批发价契约中生鲜电商平台的保鲜投入水平有所降低，而零售商的保鲜投入水平有所提高，供应链中生鲜农产品的新鲜度水平没有发生变化。

证明：与生鲜电商平台主导的批发价契约相比，在零售商主导的批发价契约中，生鲜电商平台和零售商的保鲜投入所发生的变化分别为

由式 （5.42）和式 （5.43），得到Irs＜Iss和Frs＞Fss。同时，两种博弈情形下新鲜度水平稳定值的变化分别为因此供应链中生鲜农产品的新鲜度水平没有发生变化，推论5.11得证。