热锻晶粒度演化预测模拟成果

5.4.1 概述

“成型”和“改性”是金属热锻的两个目的。成型是宏观变形过程，改性是微观组织演化过程，两者共处于高温环境中互相耦合。热锻工艺数值模拟应该包括“成型”和“改性”两个过程，这对于大型自由锻件和高性能模锻件尤为重要。

金属材料微观组织具有多种形式，如晶粒、相成分、空穴、位错、界面等各类晶体缺陷。不同的微观组织演化需要不同的条件，具有不同的规律；微观组织的演化结果决定了锻件的材料性能。材料微观组织及其演化的多样性和复杂性决定了微观组织演化数值模拟具有很大的技术难度。晶粒度是影响材料机械性能的主要因素，其演化机理比较清晰，因此预测热锻过程中晶粒度的演化成为当前微观组织模拟的最低目标。

对材料微观组织演化过程的模拟涉及微观、介观和宏观多尺度模拟技术，主要包括[¹⁰¹]：

（1）涉及纳米—微米尺度的分子动力学方法和蒙特卡罗方法；

（2）涉及微观、介观尺度的离散位错动力学方法、相场动力学方法、蒙特卡罗方法、细胞自动机法等；

（3）涉及介观与宏观尺度的有限元方法或差分方法。

前两类方法主要用于纯粹的材料科学研究。锻件晶粒度预测为宏观、介观尺度，属于第三类方法。为了预测锻件所有位置的微观组织演化规律，又不花费过大的计算量，需要三个条件：

1）合适的有限元模拟软件；

2）宏观、微观耦合的塑性本构关系；

3）针对具体材料，测量出本构方程所包含的所有材料参数。

5.4.2 热锻过程中的微观组织演化特征

1.热锻过程中的微观组织变化

（1）动态回复^[103]。动态回复几乎发生在所有金属材料的高温变形当中。它降低位错积累的速率和应变硬化程度，使流动应力趋于一个稳态值。在微观上，位错不均匀分布，进而形成亚晶。其中亚晶尺寸、稳态流动应力、硬化与软化速率相对比例都与宏观变形的温度、应变率以及原始晶粒度密切相关。

（2）动态再结晶^[103，104]。动态再结晶是一种将不断积累的位错能逐渐转化成晶界能的过程，宏观上它使应力降低，微观上它使晶粒细化。传统动态再结晶包括形核、长大两个过程，过程中新晶粒的晶界能保持不变。微观机理是：从原始晶界开始，重复形核、有限长大。另一类动态再结晶称为连续再结晶，新晶粒由亚晶转变而成，过程中晶粒尺寸不变，亚晶界能逐步增加并转变成正常的晶界能。动态再结晶的发生发展受到宏观变形的温度、应变率、应变以及材料原始晶粒度、第二相粒子分布以及合金中微量元素的多少等因素制约。例如，随着变形温度升高、应变率降低和原始晶粒度减小，动态再结晶进程加快，再结晶晶粒度增加。当变形温度升高到一定程度或应变率下降到一定程度，应力—应变曲线呈现波浪形，晶粒度的变化更为复杂，甚至出现了晶粒长大。具有柱状晶的铝合金棒材高温变形试验表明，在晶粒细化的同时伴随晶粒等轴化。事实上在高温变形过程中，晶粒的细化、等轴化与均匀化是随变形增加同时发展的。

（3）动态晶粒长大^[105，106]。动态晶粒长大通常发生在超塑性变形过程当中。这种晶粒长大是高温持久作用和晶界滑动机制变形促进长大的综合结果。一方面，超塑性变形中的晶粒长大使流动应力增加；另一方面，温度、应变率及原始晶粒度和第二相粒子分布对晶粒长大影响极大。在普通的热锻变形中也可以观察到晶粒长大，但微观机理有所不同。

（4）在高温锻造的加热、冷却过程和变形的间隙，静态回复、静态再结晶和静态晶粒长大是影响锻件微观组织和力学性能的特别重要因素^[107]。这种静态的组织变化的发生、发展由前期变形条件和原始组织决定，而静态组织变化的结果对此后的宏观变形产生重要影响。

（5）当研究粉末成型、大型钢锭自由锻或者研究热锻开裂问题时，空隙度是一个非常重要的物理量。关于空洞损伤问题已有相当多的研究文献公布，这里不再重复。在粉末成型和大型钢锭的自由锻过程中，我们希望通过变形消除空洞和疏松缺陷。在这种情况下，空隙度应逐渐缩小。与开裂过程相反，疏松和空洞的压实过程包括：大空洞分散成小空洞，小空洞闭合以及最终达到焊合彻底消除界面痕迹^[107]。前两个过程主要由变形控制，而焊合过程由热扩散控制。

（6）此外，加热和冷却过程中还可能发生相变^[108]，变形过程中织构的演变也是非常重要的微观组织变化^[108]，它们受宏观变形的控制，同时也影响宏观变形的状态。

2.高温锻造变形的微观机制 高温锻造变形是多种变形机制共存^[102]。这是因为金属材料内存在三类缺陷：点缺陷（自由电子和空穴）、线缺陷（位错）、面缺陷（晶界、相界和自由表面等）。热锻过程中的高温激活了这三类缺陷的运动，产生了不同的变形机制。例如，扩散蠕变对应点缺陷的运动；位错蠕变对应线缺陷的运动；晶界滑动对应面缺陷的运动。由于不同种类的缺陷激活能不同、运动速度不同，对材料的微观结构及合金成分的反映不同，因此在同一变形条件下，虽然可能多种变形机制共存，但是每种机制对变形的贡献是不同的，它们有主有次地协调发展，受控于外部赋予的变形条件和材料内局部的微观结构^[109，110]。当外部条件变化时，变形机制之间的主次关系也随之发生变化。很多研究者通过大量的实验给出了很多具体材料变形机制的分布图^[111]，图中变形机制作为无量纲温度和无量纲应力的函数。例如，由于扩散速度的限制，仅当应变率很低、温度很高时扩散蠕变对总体变形的贡献才能占主导地位；位错蠕变的激活能较高，在较高的应力水平上（较高应变率或较低温度），不可逆变形主要来自这种变形机制；晶界滑移是超塑性变形特有的变形机制，它仅当晶界面积足够大（等轴细晶）、温度和应变率适合时才会起主导作用。这种变形机制对晶粒度、温度和应变率极为敏感。必须指出：由于材料微观组织的不均匀性，因此即使在相同的变形温度和应变率条件下工件不同部位的变形机制分配比例可能是不同的，这种分配比例将随着外部的变形条件和内部微观组织的变化而改变。在某种外部和内部的变形条件下，可能会出现不同变形机制之间的协调失败，于是微裂纹或孔洞开始形核以适应在外部载荷的强制作用下材料质点的运动^[102]。

5.4.3 热塑性本构关系及晶粒度演化方程

宏观变形（应力、应变、温度等）是物理过程的热力学外部状态变量，微观组织是热力学内部状态变量。宏观、微观耦合的本构关系归结为4类方程：

初始与后继屈服面方程：F（σ_ij）-Y²=0。

流动应力表达式：。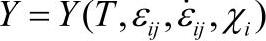

塑性变形的演化方程：

，。

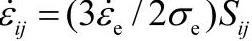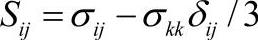微观组织演化方程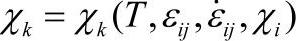：χ_k=χ_k^Tε_ijε_ijχ_i，k≠i。

屈服面方程与塑性应变增量方程在固体力学中已有大量研究。流动应力方程可通过理论推导或通过试验获取，试验曲线已经包括了微观组织对流动应力的影响。微观组织演化方程可直接引自材料科学的研究结果，或用不可逆热力学理论结合具体演化模型进行理论推导，或引用更小尺度的数值模拟结果。

在热锻过程中，晶粒演化包括尺寸演化、形状演化、晶格取向趋势等。试验证实，由于温度或变形的作用，处于不平衡状态的晶粒总是趋向其稳定状态。晶粒大小趋向其稳态晶粒尺寸，不等轴晶粒趋向于等轴晶粒；晶粒主轴方向、晶格取向趋向于逐渐与变形和应力方向协调。后者涉及织构的演化。目前对晶粒尺寸演化研究较多，涉及细化和粗化。晶粒细化与再结晶有关，晶粒粗化即晶粒长大。按照是否伴随变形又将晶粒细化、粗化分成动态和静态两类。目前在晶粒尺寸演化方面已经取得了多种形式、多种材料的演化方程，应用最多的是经验方程，下面一组典型经验方程最早由C.M.Sellers用于轧钢的晶粒度计算，后来由R.Kopp引入到锻压领域^[112]。

动态再结晶：

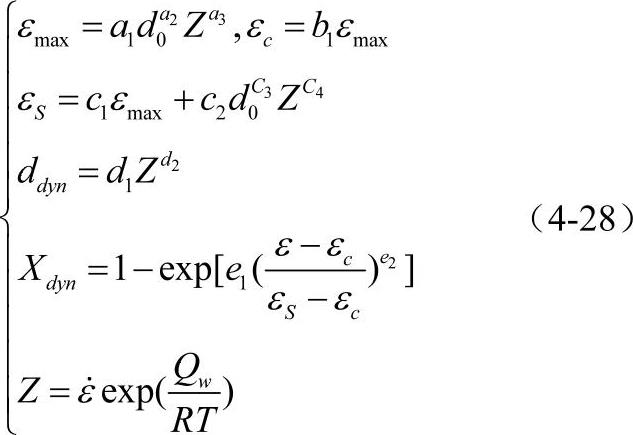
静态再结晶：

静态晶粒长大：

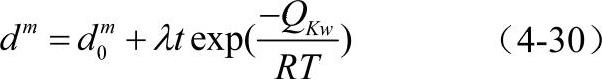
还有很多形式类似的经验公式，所有经验公式的共同点是用Avrami关系表示动态再结晶体积分数，用幂函数关系表示温度促进晶粒长大的演化规律。区别较大的在于材料流动应力与再结晶体积分数的关系表达式，其中一些人使用了混合物定律，把再结晶区和未再结晶区看成混合在一起的具有不同流动应力的两种材料。几乎所有经验公式中都只用平均晶粒度来描述晶粒尺寸。当再结晶晶粒尺寸很小、原始晶粒尺寸很大时，平均晶粒度可能会产生误导，因此还应引入一个最大晶粒度差，以弥补不足。

另一类演化方程是理论型公式^[113-115]。以下是金泉林基于不可逆热力学建立的动态再结晶本构关系^[113]。这个本构关系中包括了再结晶体积分数X、再结晶晶粒度D₂、未再结晶晶粒度D₁、最大晶粒度差D_c、平均晶粒度D等多个微观组织演化方程：

晶粒静态长大的规律已有大量试验结果和公认的经验公式，如式（4-30）所示。动态晶粒长的规律已经引起注意。例如很多材料出现多峰型应力—应变曲线时有动态晶粒长大发生，这时的稳态晶粒尺寸是大于初始晶粒尺寸的。实验证明，随应变增加，晶粒逐渐趋于稳态晶粒尺寸。另外一类的动态晶粒长大是超塑变形条件下的应变促进晶粒长大。钛合金、铝合金细晶超塑性都存在这种现象。金泉林已经给出了这类晶粒长大的演化方程^[116，117]：

5.4.4 Z参数

对于钢和多种合金，Z参数在描述微观组织演化方面起着重要作用。但是镍基高温合金的晶粒度演化与Z参数的相关性很差，如图4-58所示，原因在于高温合金对温度更敏感，对应变速率不敏感。

参考文献[118]建议了一个新的Z参数，，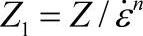

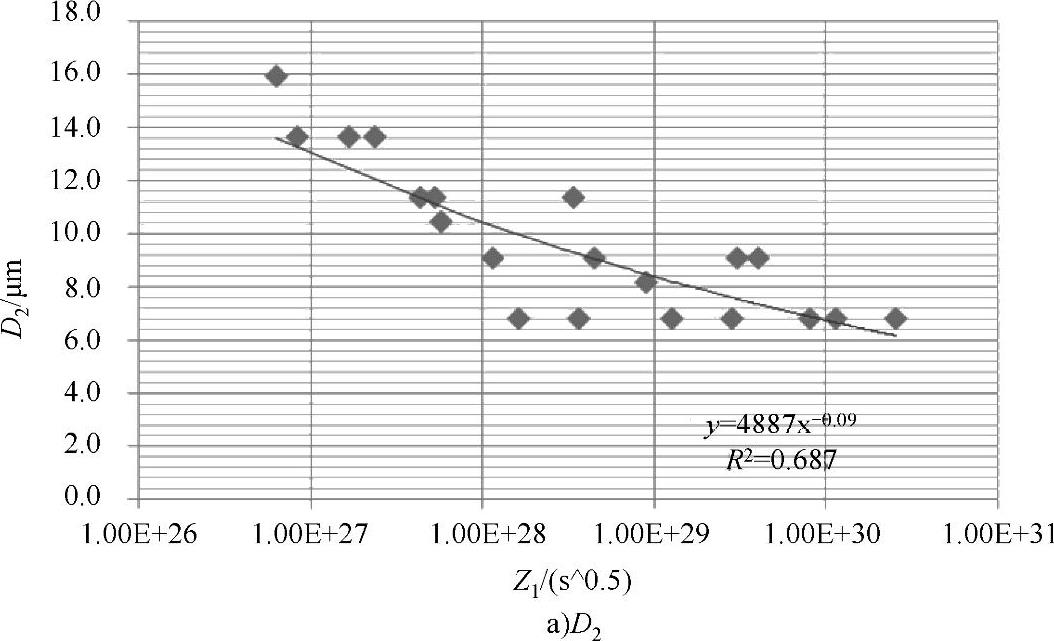
式中n＞0，这样的形式可以改变Z对于应变速率的依赖关系，n的取值可能与具体材料牌号状态有关，对于GH4169，n=1.5。使用新的Z参数，改善了GH4169高温合金载再结晶晶粒度D₂、再结晶体积分数X、平均晶粒度D方面与新Z参数的相关性，如图4-59所示。

图4-58 高温合金的D₂与Z的关系很分散

(www.xing528.com)

图4-59 D₂、X、D与新的Z参数Z₁的关系

图4-59 D₂、X、D与新的Z参数Z₁的关系（续）

5.4.5 材料本构参数识别

使用刚塑性模型进行一般的热锻工艺模拟，只需输入一组不同温度、不同应变速率下的应力—应变试验曲线即可。当需要模拟微观组织演化时，无论使用何种本构关系，都需要输入与微观组织演化有关的材料参数。因为涉及多种微观组织演化过程，所以要进行各类不同试验的参数协调，这是很困难的事情。为此使用了反分析算法，通过试验和有限元相结合，应用优化算法获取所要的本构参数。这种方法的思路如图3-4-60所示。通常采用优化算法，根据计算结果与试验结果的误差（目标函数值）修改参数。对于简单问题（例如超塑性成型），可以使用局部优化方法，对于复杂问题（例如普通热锻），则需要用全局优化算法。一个专业程序使用了局部优化和遗传算法相结合的全局算法，其简略框图如图4-61所示^[119]。

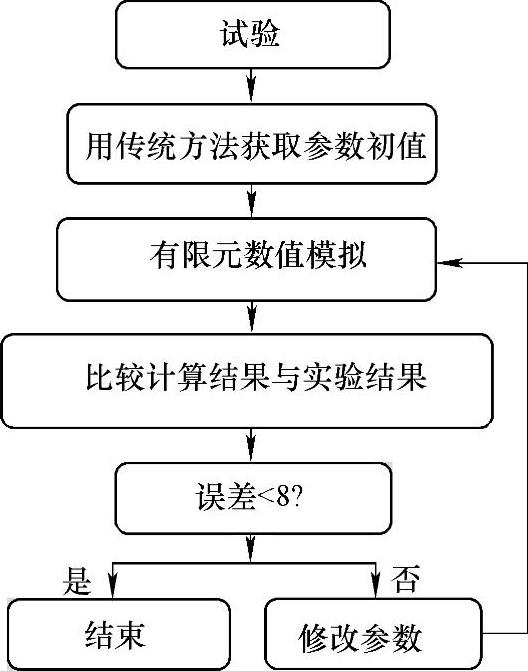
图4-60 反分析算法的思路

5.4.6 热锻晶粒度演化模拟软件

热锻晶粒度演化与各种热力学变量的关系是非线性的复杂关系，它们需要非线性迭代求解。普通刚塑性有限元软件处理宏观变形与温度耦合需要两层迭代，加上微观组织模拟以后，它们之间的耦合作用则需要三层迭代（见图4-62）。这是因为温度、速度、晶粒度是三个彼此独立的变量，需要单独求解， 三层迭代是为了保证它们之间的相互耦合。如果将原有限元程序的变分原理的速度变量扩展到速度和晶粒度变量，则可以减少一层迭代。

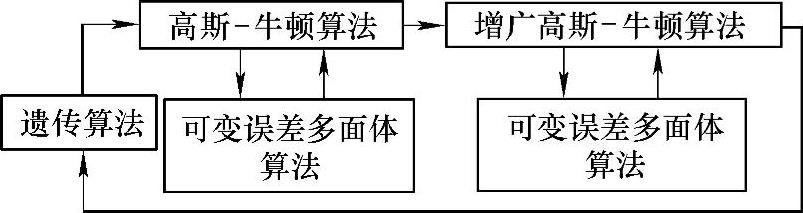
图4-61 全局优化算法框图

5.4.7 算例

（1）圆柱体热压缩试验^[120]。对转子钢26CrNi4MoV的圆柱体热镦粗试验过程进行数值模拟，试验尺寸为φ8mm×12mm，材料初始晶粒度为275µm，最大压下量为33%。压下速度为0.012mm/s，温度为950℃。 模拟软件为SF2D。因为轴对称和上下对称，模拟结果中只显示1/4个试样剖面。转子钢圆柱体热压缩试验晶粒度演化模拟结果说明，在模具接触的死区，应变为零，未发生动态再结晶，晶粒度保持不变；在心部，变形最大，再结晶完成最多，体积分数最大值达到99%，平均晶粒度最小48µm，晶粒度最均匀，其最大晶粒度差仅为0.8µm；在试样肩部，虽然应变较大，但是因为应变速率较高，因而再结晶体积分数并不大，并不是细晶区；试样外侧，应变不太小，再结晶发展较好，属于细晶区；心部再结晶晶粒度最小，靠近边界再结晶晶粒度增大；靠近变形死区和自由边界处最大晶粒度差较大，是容易出现混晶的地方。图4-63所示为转子钢圆柱体热压缩试验平均晶粒度模拟结果与试验对比，可以看出，模拟结果与实验结果符合较好。

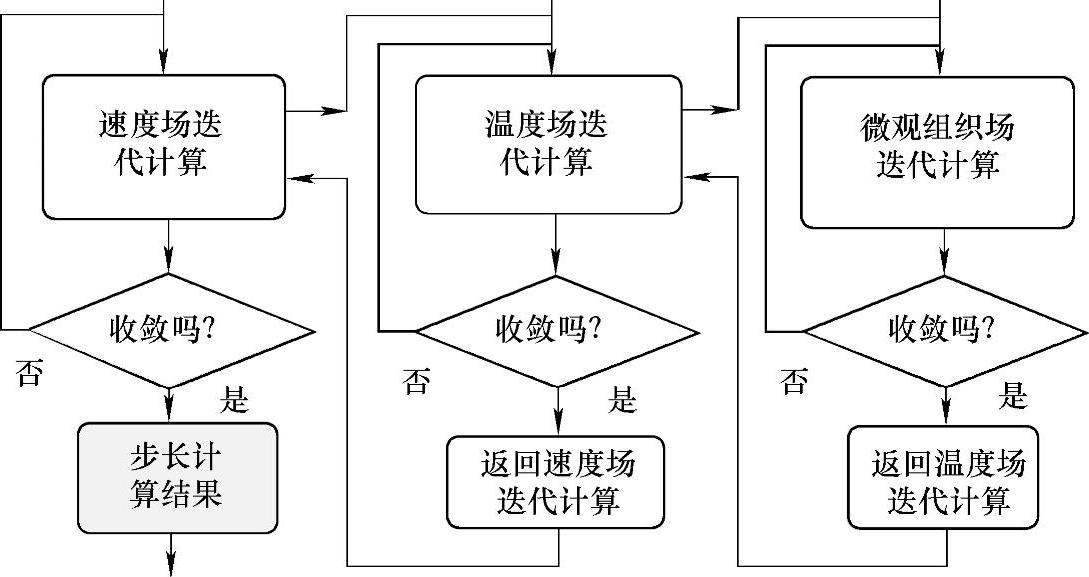
图4-62 微观组织模拟算法多层迭代^[97]

图4-63 转子钢圆柱体热压缩试验平均晶粒度模拟结果与试验对比^[120]（压下量=33%，初始应变率=0.001/s，温度=950℃，初始晶粒度=275µm）

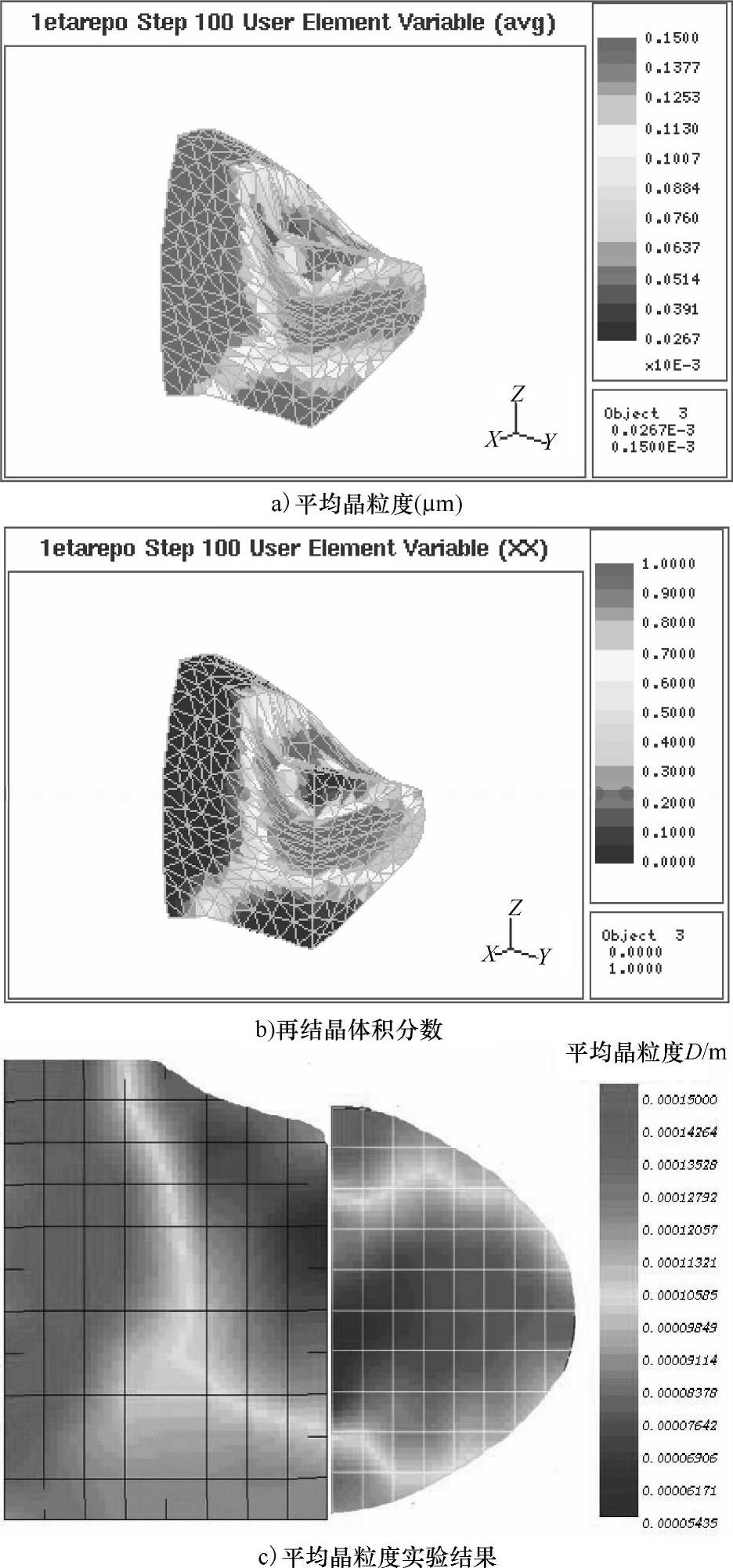
图4-64 FMV砧拔长工艺模拟与晶粒度演化预测结果（压下量=38.9%，上模速度=0.3mm/s，温度=1000℃）

（2）FMV砧拔长工艺实验与模拟^[121]。图4-64所示为FMV砧拔长过程中平均晶粒度与再结晶体积分数的数值模拟结果。FMV工艺是一种上窄、下宽不对称的大圆角135°V砧拔长工艺。钢锭的模拟试样为圆柱形，尺寸为φ9mm×10mm，材料为26Cr2Ni4MoV转子钢，初始晶粒度为150µm。上、下砧宽比例为1：2，为135°V型砧。上砧速度为0.3mm/s，上砧压下量为38.9%，摩擦系数取值0.3，试样初始温度为1000℃。由于砧子、工件前后左右的对称性，所以模拟计算只对1/4工件进行。计算中使用的模拟软件为二次开发的DEFORM3D。所用本构方程为式（4-31）～式（4-33）。结果显示，只有工件心部和与砧子边缘接触位置发生明显再结晶和晶粒细化。图4-64c和图4-64d给出了工件纵、横截面平均晶粒度分布的实测结果与计算结果的对比。其中左半部分表示试样的纵剖面，右半部分表示试样的横剖面。可以看出，模拟结果与试验结果的分布形态完全一致，定量上也吻合较好。两者外形的一些差别源于砧子的轻微变形以及试样剖分的位置偏差。

（3）镁合金反挤压工艺模拟[¹²²]。图4-65所示为镁合金AZ31D零件超塑性反挤压工艺数值模拟和晶粒度演化预测。模拟软件为二次开发后的DEFORM2D。

图4-64 砧拔长工艺模拟与晶粒度演化预测结果（压下量=38.9%，上模速度=0.3mm/s，温度=1000℃）（续）

图4-65 镁合金AZ31D超塑性反挤压工艺实验与数值模拟结果^[122]

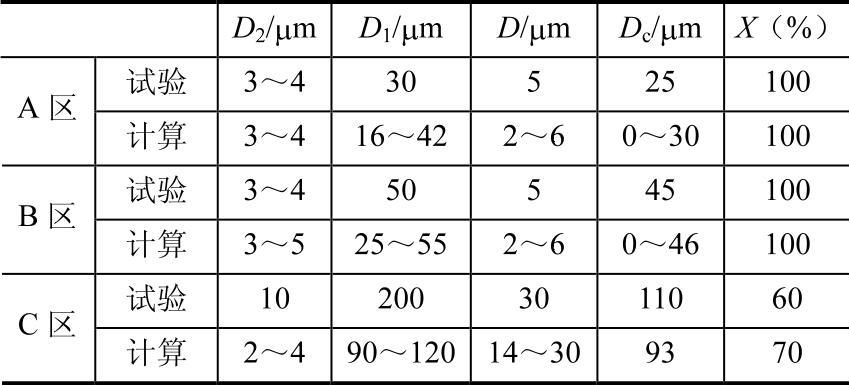
本构方程为式（4-31）～式（4-33）。图4-65a展示了成型后零件剖面照片以及3个典型位置的金相照片。镁合金坯料为近似圆柱形，初始晶粒为大于100µm的柱状晶粒。为了提高成型件的性能，希望通过坯料和模具的优化设计，使工件内部发生动态再结晶和晶粒细化。金相照片显示这个目的达到了：A区再结晶已经完成，平均晶粒度小于10µm；B区再结晶基本完成，平均晶粒度小于10µm，但是晶粒度均匀性不如A区；C区未完成再结晶，仍然是有直径接近40µm的粗大柱状晶，平均晶粒度超过20µm。图4-65b和图4-65c给出了这个反挤压零件平均晶粒度、再结晶体积分数的数值模拟结果。表4-15给出A、B、C三个区内模拟结果与实验结果的对比，可以看出，模拟结果与实验结果在定量上符合得很好。

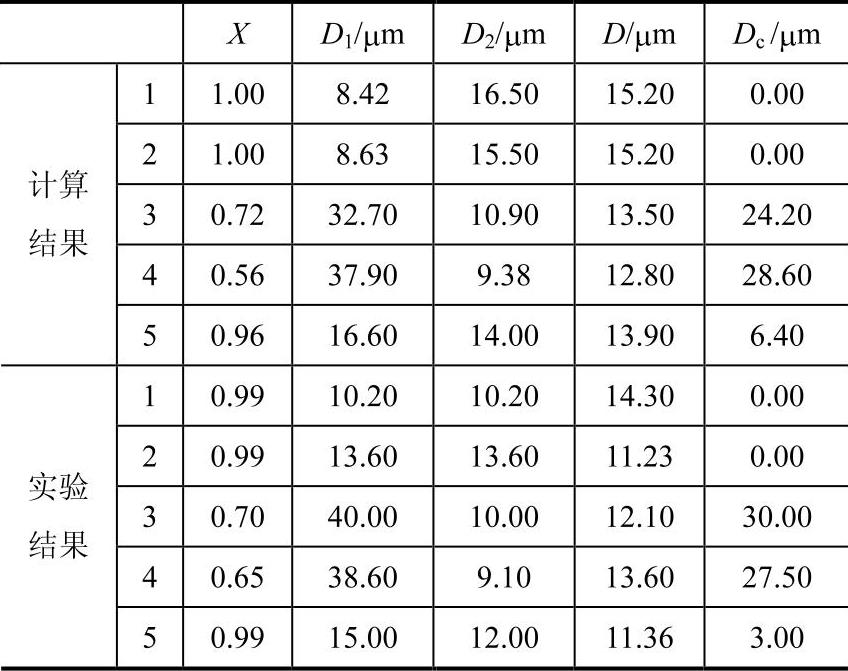
（4）高温合金涡轮盘热模锻工艺模拟[¹²³]。图4-66所示为GH4169高温合金涡轮盘热模锻晶粒演化预测结果。零件材料为GH4169，毛坯尺寸为φ326mm×145mm。毛坯涂玻璃润滑剂，设定摩擦系数=0.01。上模总行程为114mm，压力机上模平均速度V=0.95mm/s。实际成型的涡轮盘沿径向剖分并进行晶粒度观察，选出5个典型

表4-15 AZ31D反挤压成型件微观组织预测与实验结果的对比

位置进行各个晶粒度变量的测试。图4-66a中点表示所选出的5个测试点的位置。其他两个图为再结晶体积分数X、平均晶粒度D的模拟结果。表4-16列出这5个测试点晶粒度实验结果和计算结果的对比。可以看出，数值计算结果与实验结果符合很好。首先数值模拟和实验结果给出的再结晶和晶粒度演化趋势相同：盘件中心区域的1、2、5三点再结晶完成比较充分，晶粒度比较均匀，平均晶粒度误差小于4µm。盘件轮缘区域的3、4两点再结晶未完成，存在明显粗大晶粒，晶粒度不均匀。平均晶粒度略小，最大晶粒度差达到9～10µm。实验结果与计算结果绝对误差都达到了可接受的程度。

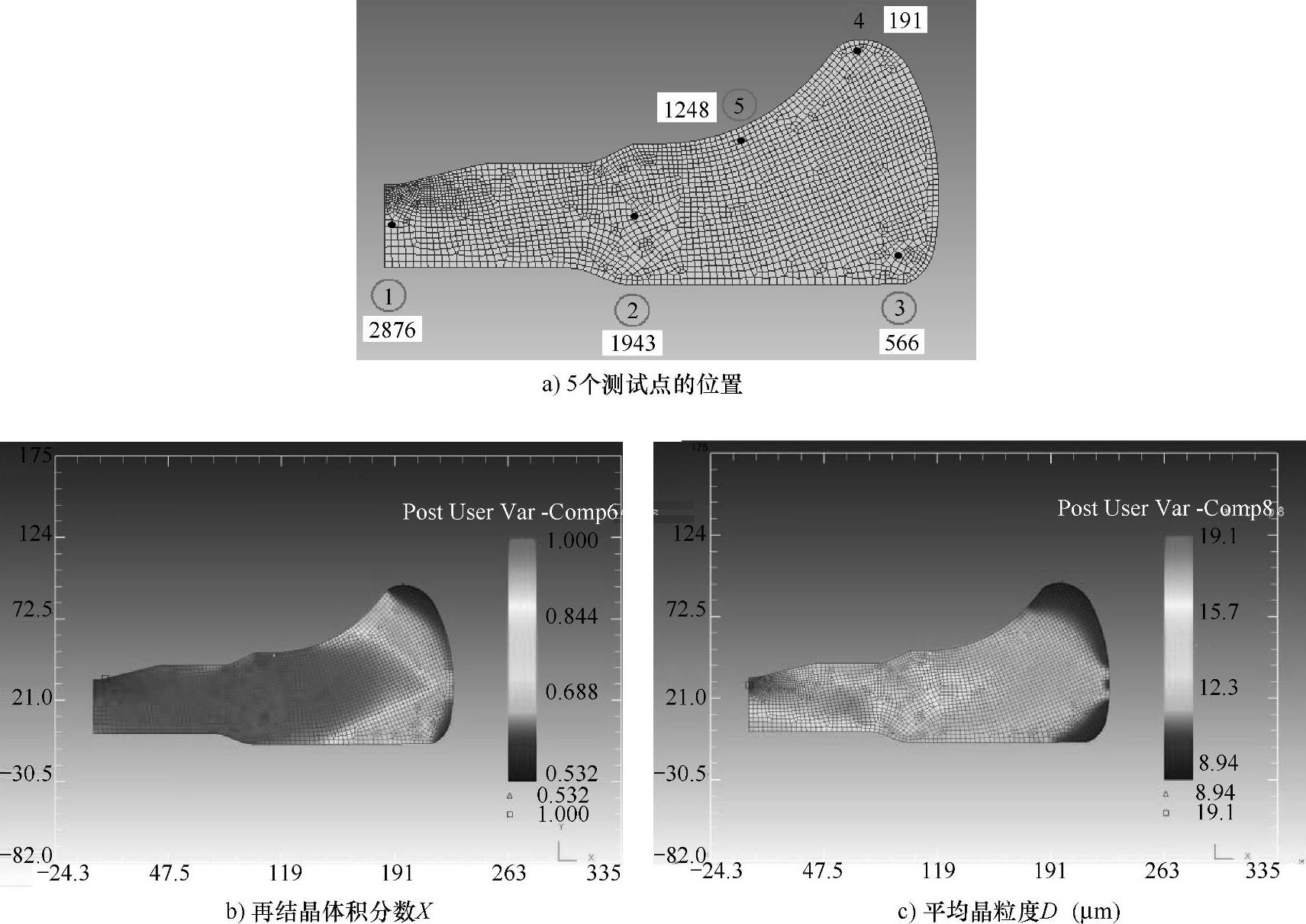
图4-66 GH4169高温合金涡轮盘热模锻晶粒演化预测结果

表4-165 个测试点的计算结果与实验结果对比

（5）大型汽轮机低压转子热锻全过程晶粒度演化模拟^[123]。图4-67a所示为低压转子锻打台阶轴时平均晶粒度的模拟结果。这一火次使用上平下V砧，锻打时锤间间隔时间为30s，计算时假设如果应变速率<0.0001/s，则认为属于静态。图4-67a显示1/4转子剖面的平均晶粒分布。可以看出水口端因锻打晶粒细化，中段晶粒较大，钳口端晶粒最大。图4-67b所示为晶粒演化3种状态分布图。由图4-67b可以看出，端部锻打部位属于3区（再结晶），轴中段和钳口端属于1区（静态晶粒长大），两者交接处为2区（动态晶粒长大），可以看出2区面积极小。

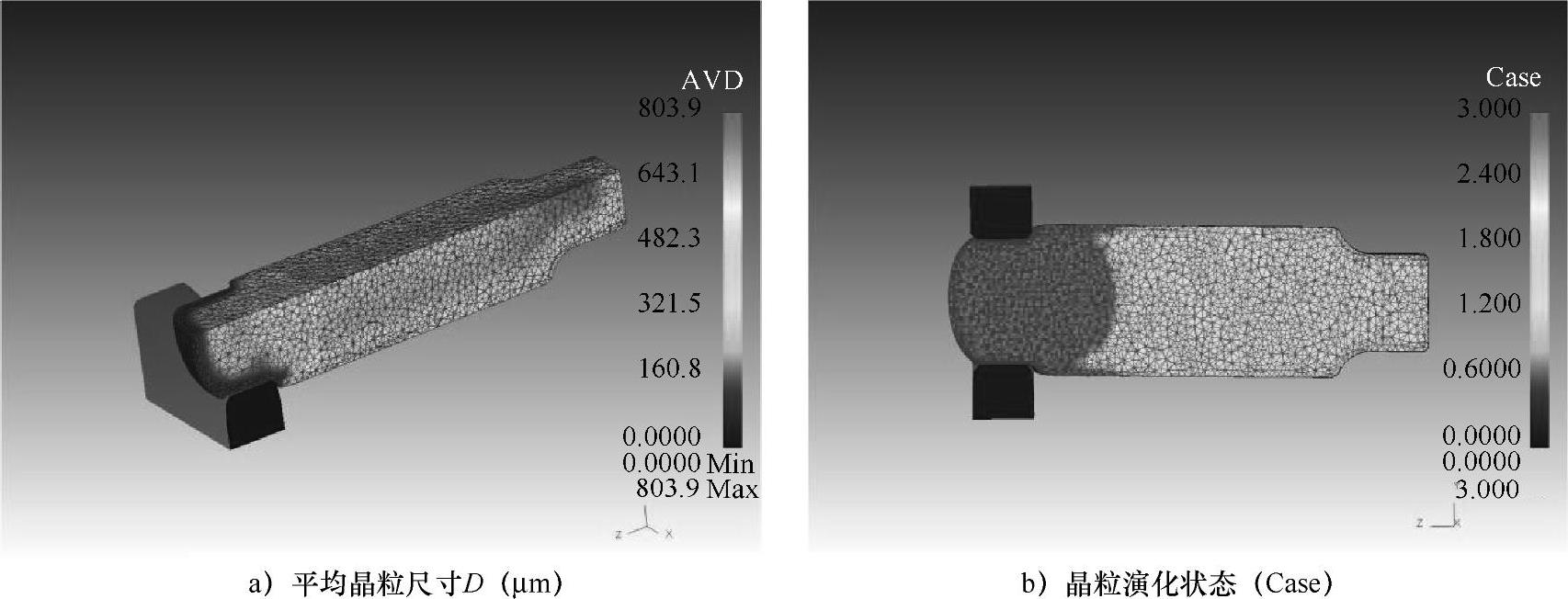
图4-67 锻打第一周结束后平均晶粒度D与晶粒演化3种状态

注：Case=1，静态长大；Case=2，动态长大；Case=3，动态再结晶。

（6）高强钢模锻件晶粒演化数值模拟。图4-68所示为一个成型后模锻件的平均晶粒尺寸和再结晶体积分数分布图。坯料炉内加热温度为1140℃，模具初始温度为400℃。坯料从炉内取出再放入凹模温度略降，开始锻造时模具温度已经不是均匀分布了。工件与模具温度都随时间变化，所以工艺模拟含热传导计算。工件模具之间摩擦系数=0.1。合模后工件平均晶粒最小值为20µm，中间部位最大值不超过80µm，多数区域平均晶粒度在30～40µm范围内。除了中间头部区域以外，锻件大部分区域的晶粒度比较均匀，最大晶粒度差为60µm以下。得到的结论是：过于复杂的坯料形状可能引起锻件不均匀变形，不均匀动态再结晶过程以及不均匀晶粒细化过程；坯料不同部位变形开始的时间有很大差别，造成了再结晶和晶粒细化过程的很大差别，甚至在变形初始时刻很大部分区域出现了晶粒长大，最早与最晚的再结晶过程相差350个时间步。

（7）避免晶粒异常长大和混晶缺陷的工艺措施^[124]。已经发现，大型汽轮机低压转子在传统锻造过程中钢锭心部温度始终大于1150℃，在成型火次锻件中段又处于无锻造比加热状态，持续高温造成了晶粒异常长大，转子钢的遗传性很强，锻造阶段形成的粗晶组织会给后续正火带来困难或引起混晶缺陷。根据低压转子锻造过程晶粒度演化的模拟，提出了改进工艺措施，基本思路是锻造过程中适当控制炉温和保温时间并进行合理空冷降温，确保锻件中心温度低于晶粒异常长大的临界温度，又不影响正常锻造变形。这一思想已授权发明专利（专利号ZL：200510114420.3），并进行了生产实验验证，新工艺可将原来的3次正火减少一次正火。专门针对1000MW核电低压转子的压实工艺和晶粒度控制的发明专利也有类似的原理（专利号：ZL 200610146679.X）。

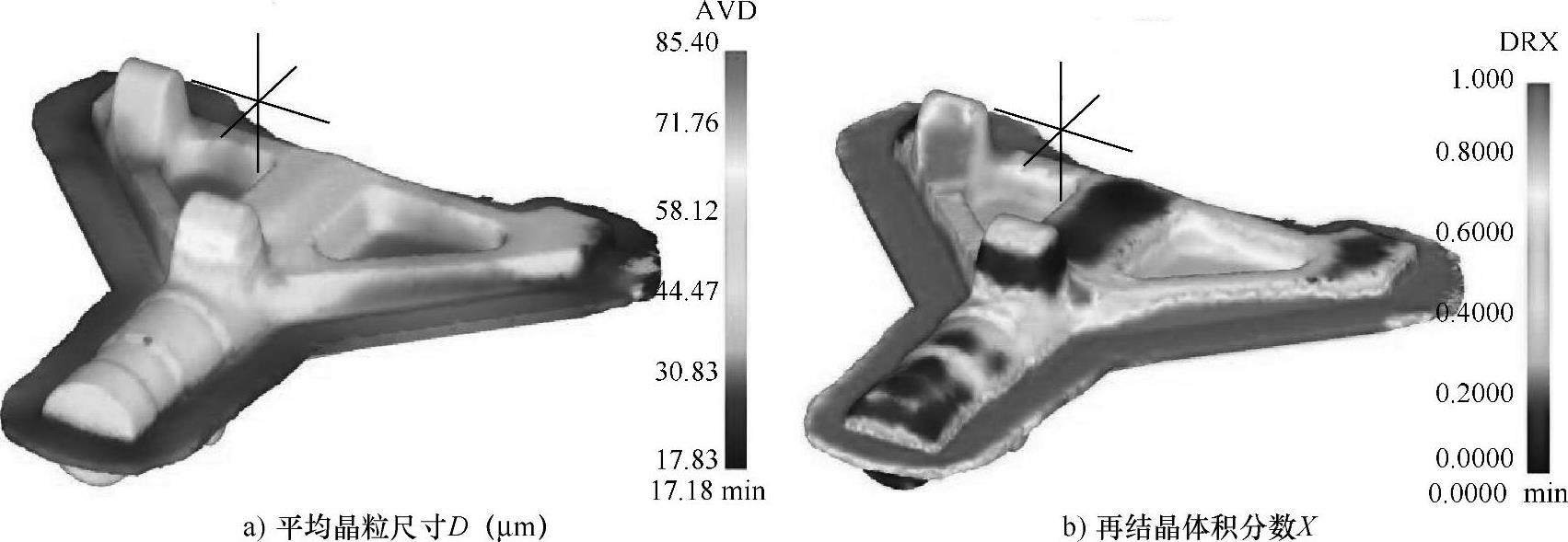
图4-68 某高强钢模锻件成型后平均晶粒尺寸和再结晶体积分数分布图

图4-69给出了1000MW核电低压转子第一道成型火次锻打第一周后新老工艺的锻件晶粒度分布。由于新工艺将锻件心部的温度控制在1150℃以下，最低值为1124℃，避免了晶粒异常长大，锻件心部晶粒度从未超过700µm。而老工艺锻件心部温度始终大于1200℃，最低值为1222℃，心部晶粒长大严重，晶粒度超过了2200µm。这就验证了所建议的锻造工艺措施可以预防1000MW汽轮机低压转子出现混晶缺陷。

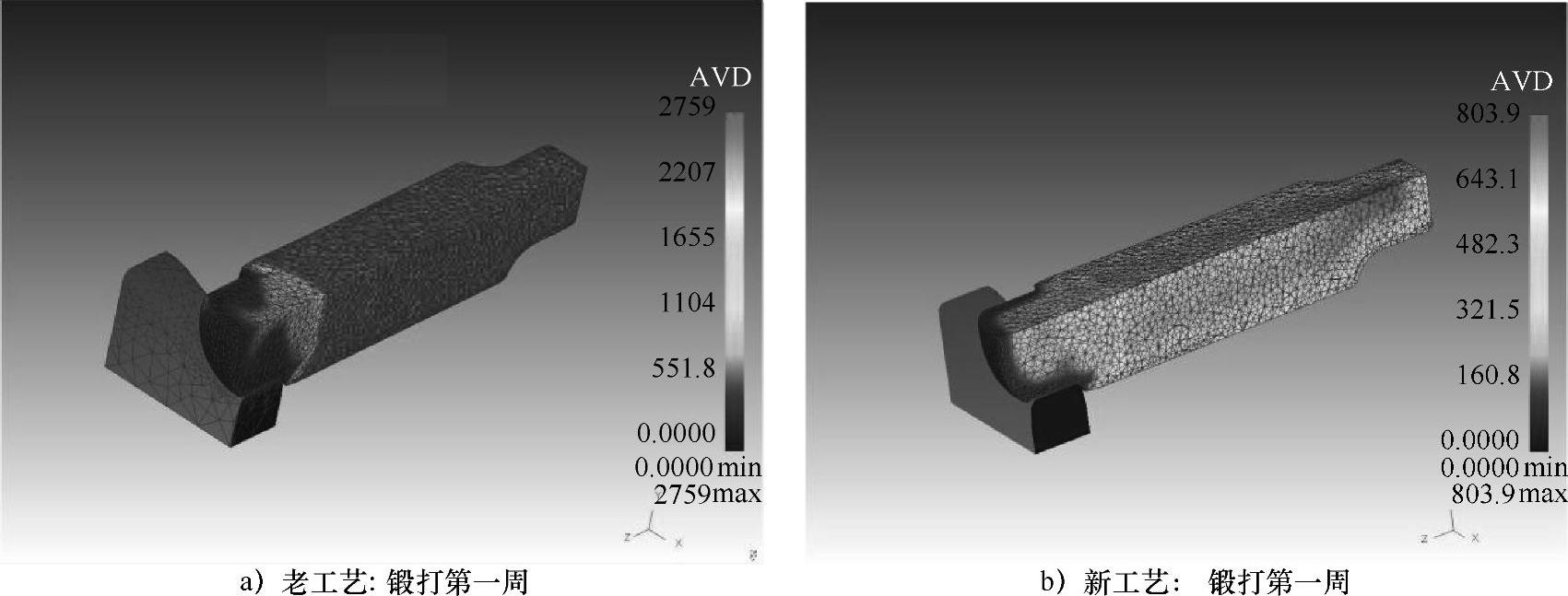
图4-69 锻打第一个台阶轴时锻件平均晶粒度分布

注：沿中心轴剖分，显示四分之一个锻件。