5.3.1 概述
这里所说的锻造工艺数值模拟指的是所有塑性体积成型的工艺模拟,它包括各类锻造、挤压、回转成型等。按照模拟软件是否需要传热计算,可以分为冷锻、热锻、等温锻等。传统的锻造工艺模拟只模拟工件的变形过程,不模拟成型过程中工件微观组织的变化。因此传统的锻造工艺模拟的理论基础是传统的弹塑性变形理论,其中热锻工艺模拟的理论基础是热—力耦合的热弹塑性变形理论和热传导理论。本节只考虑这种传统的冷、热锻造工艺模拟,那种考虑热锻过程微观组织演化的热锻过程数值模拟将在5.4节专门讨论。这种基于弹塑性力学的普通锻造工艺模拟起源于20世纪70~80年代,与大多数需要解决的实际工程问题相比,软件的理论、算法、应用三个方面的发展已经比较成熟,软件在制造业获得了广泛的应用。著名的专业商业软件有DEFORM、QFORM、MSC/MARC/AUTOFORG、MSC/SUPERFORGE、FORGE等。近年来这些商业软件功能都有了较大发展,例如DEFORM、FORGE增加了热锻过程动态再结晶预测功能和淬火热处理功能,虽然所用的材料模型还过于简单。在接触搜索、网格重化加密方面也有很大进步,例如MARC/AUTOFORGE开发的六面体网格加密和重划模块已经成功应用多年。现在大多成型模拟软件都可以对锻造工艺全过程的多道工序进行连续数值模拟。大多数模拟软件都具有疏松材料变形过程的数值模拟功能,这方便了粉末冶金坯料的锻造和大型钢锭疏松缺陷压实过程的模拟,没有考虑疏松缺陷压实后的扩散焊合过程是需要改进之处。
5.3.2 实体单元类型
锻造工艺模拟所用的是三维或二维实体单元。二维情况包括平面应变单元、平面应力单元和轴对称单元。常用的二维单元有3节点线性单元、4节点双线形单元。虽然有些软件也包括5节点、8节点、9节点单元,但是最常用的是4节点四边形等参单元,这种单元优点是计算量低、形状协调性好,双线性精度不太低。常用的三维实体单元包括4节点4面体常应变等参单元和8节点六面体双线性等参单元。大多数锻压模拟软件都采用4节点4面体单元,这是常应变单元,只有少数软件(MARC/AUTOFOGE)使用8节点六面体单元。这是因为4节点四面体单元网格加密的算法比较简单,而六面体单元网格细化加密具有太大技术难度,目前只有MARC/AUTOFOGE软件具有这类六面体网格重划和加密的模块。选择二维还是三维单元时要注意,所有要模拟的实际问题都是三维问题,只有所模拟的问题满足一定条件时才能简化为二维问题,例如平面应变与平面应力条件是完全不同的两种条件,使用时不要搞混弄错。
单元的插值形函数取决于单元的形状、节点类型、节点个数。C0型(Lagrange型)单元在边界上只要求位移函数连续,而C1型(Hermite型)单元在边界上则要求位移函数及其一阶导数连续。通常选择多项式幂函数作为单元插值形函数,C0单元内线性位移分布只需用角点位移表示。对于C1单元,节点参数需包括节点位移及其一阶导数。显然多项式幂阶越高单元位移函数精度越高,就可以获得更高级别的导数连续,但是为了确定其中的待定参数所需要的单元节点数也越多。低阶单元计算速度快,但是单元的位移函数最低应满足:包含刚体位移和常应变;单元边界位移连续。通常软件主要使用等参单元,即位移ui函数插值公式与位置坐标xi变换公式都用相同的形函数与节点参数进行插值:
图4-53所示为常用三种常用单元示意图,三种常用等参单元的插值形函数如下:
1)二维4节点四边形单元。
2)三维4节点四面体单元。
3)三维8节点六面体单元。
这三类单元都是线性单元,虽然有更高阶单元,因为单元节点数较多,精度提高需要付出增加计算量的代价,因此应用低阶单元、减小网格尺寸也可达到提高精度的目的。
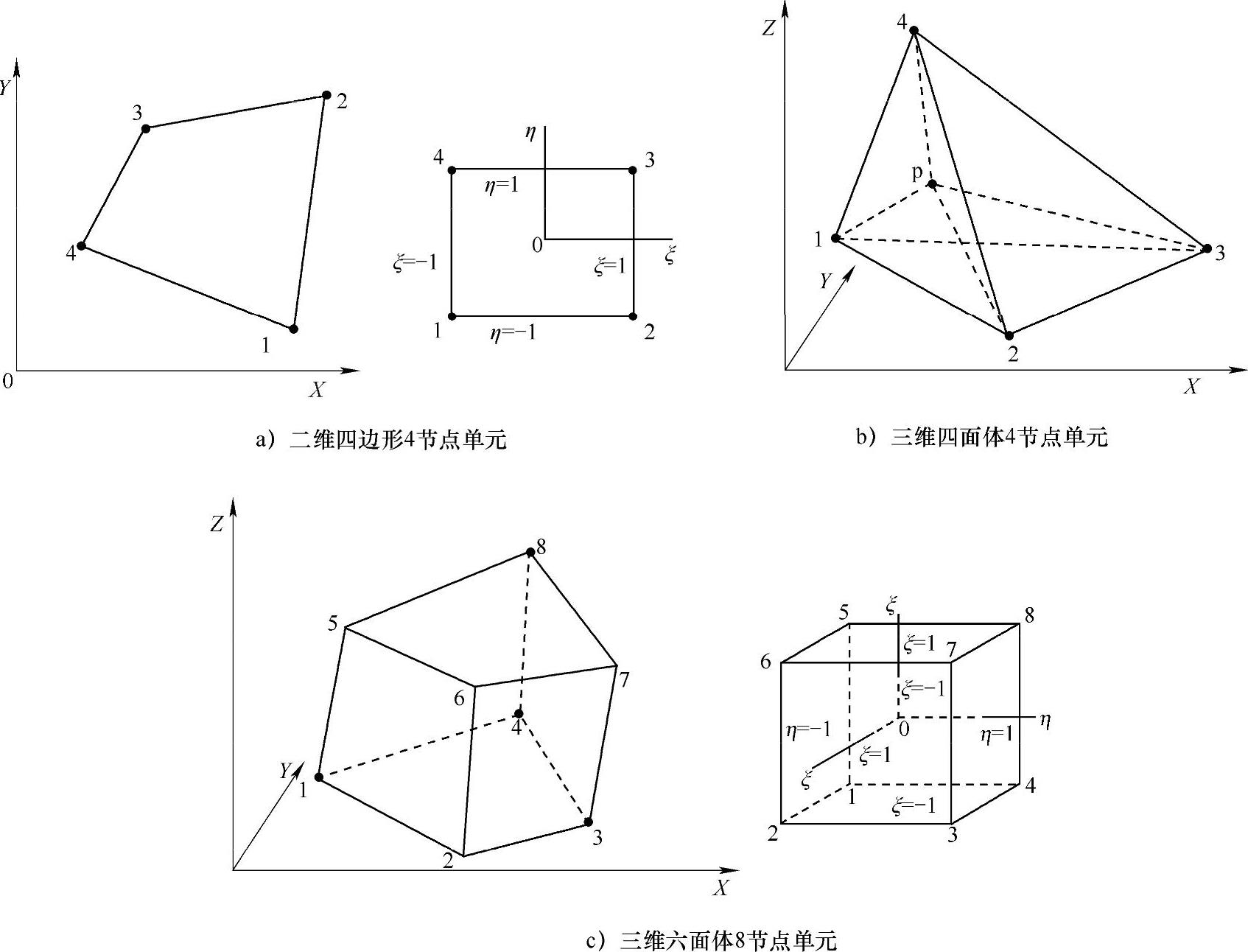
图4-53 三种常用的线性等参单元
5.3.3 材料本构关系与破裂准则
在冷热锻造工艺模拟软件中,用户将遇到多种材料塑性本构关系。不同的本构关系适合不同问题的模拟,正确选择本构关系对获得正确的模拟结果极为重要。
1.弹性本构关系与热弹性本构关系 在锻压工艺模拟中,弹性本构关系和热弹性本构关系只用于锻造过程中模具的应力分析,热弹性本构关系则用于热锻过程中热模具的应力分析。因为弹性变形是线性变形,来源于锻件变形抗力的模具载荷随模具位移增加而增加,因此模具应力分析可以只在锻压最后一步进行,或者在最大载荷时进行。因为是弹性分析,分析结果可以显示应力超过材料屈服强度,不会显示实际模具被压塌时所出现的大幅度塑性变形。热锻时需要连续模拟模具的温度场随时间的变化,并利用这些模具的温度数据进行模具应力分析。热弹性分析所需要的模具材料的弹性参数是温度的函数。因为加工前模具材料经过多次锻打,因此可以假设为各向同性材料,使用各向同性的本构关系。
2.弹塑性本构关系与热弹塑性本构关系 对于冷锻工艺模拟需要使用室温下弹塑性本构关系,在温锻和热锻中使用热弹塑性本构关系。在热状态下,总应变应等于弹性应变、塑性应变和热应变之和,后者是温度增加引起热膨胀变形。以一个大尺寸厚板模锻成型工艺为例,如图4-54所示,热成型出模以后厚板零件放在支架上,随着温度的降低,零件形状发生变化。造成这种形状变化的应变分量有:出模以后压力撤销造成的回弹、零件自身重力与支架支点反力产生的弹塑性变形、零件不均匀降温引起的热应变,为了预测这种工况的变形必须使用热弹塑性本构关系。
因为弹性变形和塑性变形加、卸载的应力、应变规律不同,有限元计算时需要区分弹性区、塑性区,需要确定弹塑性边界的变化,这需要多次迭代并耗费很大存储空间和很大计算量。因此计算一个弹塑性问题所耗费的时间相当于计算几百个、上千个弹性问题的时间,如果再加上温度场计算及其与变形的耦合,计算量就更大。注意到锻压过程中零件的塑性变形远远大于弹性变形,因此如果只考虑成型零件的形状尺寸,则可以忽略弹性变形,使用刚塑性本构关系。但是如果锻造工艺模拟的目的是关注锻件的残余应力、锻造载荷、锻件出模后的回弹影响,那么就必须要用弹塑性本构关系或热弹塑性本构关系。对于冷锻或温锻,需要确认由挤压棒材加工的坯料是否具有各向异型,如果各向异性明显就要使用各向异性弹塑性本构关系。对于普通的热锻、等温锻、超塑性锻造,弹性变形影响可以忽略不计,坯料的各向异性也可以忽略不计。大多数金属材料都具有应变硬化效应,通常有各向同性强化、运动学强化以及两者复合的混合强化三种模型来描述这种应变强化效应,其中运动学强化对应材料的包辛格效应。需要注意所选择的本构关系特征要和所使用的坯料性能相符合。当锻造使用粉末制坯时,由于坯料具有可压缩的特征,其强度和其他力学性能参数都随相对密度而变化,所以要用专用的疏松材料弹塑性本构关系。在这个本构关系中应力塑性屈服面与应力的第二不变量和第一不变量有关,也与材料的相对密度有关。而普通的实体材料弹塑性本构关系的塑性屈服面只与应力第二不变量有关。金属高温变形具有明显的黏性特征,即应力随变形速率增加而增加,所以高温锻造工艺模拟所使用的本构关系应包括黏性效应。需要注意的是,在实验测试本构方程中的材料参数时,所选的实验材料应与锻压工艺实际坯料以及材料的热处理状态完全相同。否则数值模拟结果会产生很大偏差,甚至根本就不可用。一个实体材料混合强化的弹塑性本构关系如下:
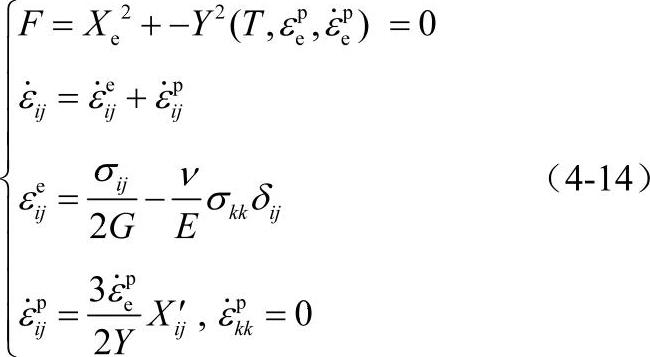
其中
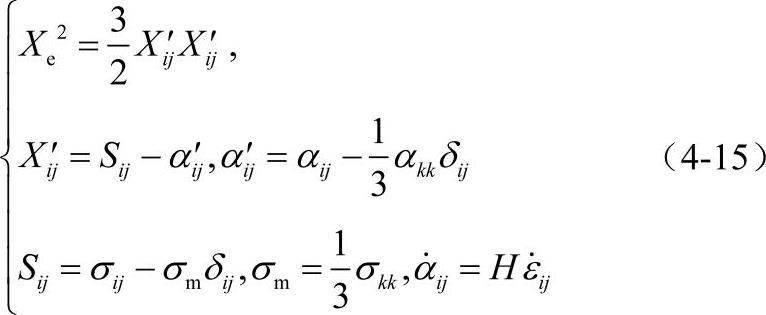

图4-54 某厚板零件热成型出模后的照片
3.刚塑性本构关系与刚黏塑性本构关系 使用刚塑性本构关系的条件是可以忽略弹性变形影响、残余应力影响和回弹影响。对于以锻件形状预测为目的的锻造工艺数值模拟是满足这些条件的。对于普通的热锻工艺模拟,因为金属高温变形表现出很强的黏性及应力对应变速率敏感,所以要使用热刚黏塑性本构关系。需要说明的是,刚塑性假设意味着忽略弹性变形,由于弹性应变与应力的线性关系以及刚性区零应变的假设,因此使用刚塑性本构关系进行工艺模拟、应力预测和载荷预测是不准确的,它只是一个上限解。使用刚塑性本构模型,通常温度变化引起的热应变也被忽略,因此所预测的应变只有塑性应变,当然回弹也就被忽略了。为了弥补刚塑性分析对应力分析的缺陷,很多软件增加了材料应力应变关系曲线输入的模块。在这种情况下流动应力作为温度、等效应变速率、等效应变的函数是由一组数据来表示的。计算时应用插值方法由温度、等效应变速率、等效应变计算出等效应力数值,将其代入应变增量的表达式,计算出应变增量。下面是一个考虑混合强化、允许疏松材料刚塑性本构关系,对于实体材料,式中的孔洞体积分数f=0,A=3,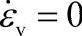 ,
,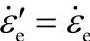 ,其中空洞体积分数f与相对密度
,其中空洞体积分数f与相对密度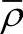 和体积应变率
和体积应变率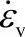 的关系为[97]
的关系为[97]
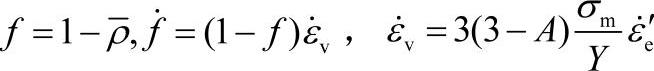
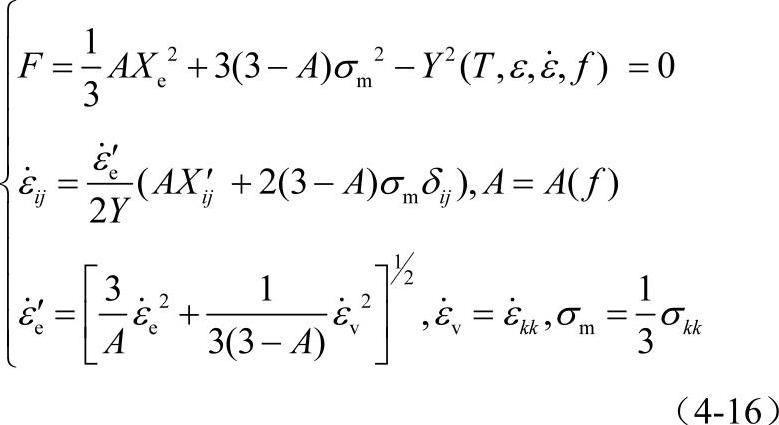
4.材料的破裂准则 预测锻造过程中的锻件开裂缺陷是锻造工艺数值模拟的重要目的之一,这就需要在软件中有一个根据温度、应力、应变状态判断锻件开裂与否的准则。材料抵抗开裂的能力是材料自身的物理特性,它与材料种类和材料微观组织密切相关。大量的实验显示,三向拉应力和降低温度将促进材料破裂,三向压应力将抵抗材料破裂。一个常用的表征材料破裂可能性的物理量称为损伤因子,当损伤因子达到一定临界值Df时,材料发生开裂,此临界值Df表示了材料的最大变形能力。损伤因子的定义为[98]

上式中包含最大拉应力σ*,等效应力σe,等效应变εe。通过拉伸试验和测试延伸率可以测试出损伤因子的临界值。这个破裂准则也可以应用到热锻中,只是在热锻情况下Df是温度和应变速率的函数,需要作不同温度、不同应变速率的拉伸试验。对于一维拉伸试验,以δ表示延伸率,则有σ*=σe,Df=δ。
5.3.4 有限元核心算法
锻造工艺有限元模拟软件全部采用静态隐式算法求解有限元代数方程,即式(4-2),因为忽略惯性项和黏性项,式(4-2)的静态形式为
KU=F (4-18)
因为非线性,系数矩阵K是位移U的函数,式(4-18)需要迭代求解。最常用的迭代方法是Newton-Raphson法或其修正法。N-R迭代的基本依据为切线刚度法,改写式(4-18)为φ(U)=KU-F=0,迭代公式为
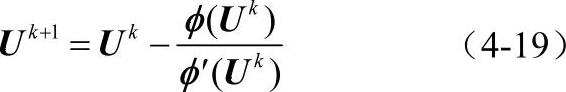
在锻造过程中,成型载荷是通过模具或砧子逐渐加上去的,因为非线性,工艺模拟也必须按时间步逐个进行,可以等步长也可变步长。在每个时间步长内进行方程迭代求解。在某一个时间步长内,物体有初始应变、初始应力,且工件内的单元可能是弹性或刚性状态,也可能是塑性状态。载荷增量或应变增量可能使单元的状态改变:弹性(刚性)单元或保持不变,或变成为塑性单元;塑性单元或保持塑性或卸载为弹性(刚性)单元。因此需要判断单元的状态变化,在组建刚度矩阵K时要根据单元的弹塑性状态使用相应的本构关系。以下分别对弹塑性本构关系、刚塑性本构关系简述迭代求解方程的有限元算法。
1.使用增量型弹塑性本构关系[95]
弹性状态:dεij=dεeij。
应力、应变关系:dσij=Dijekldεkl (4-20)
状态检查:
如果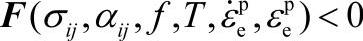 ,则保持弹性状态;
,则保持弹性状态;
如果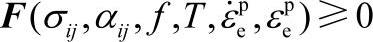 ,则进入塑性状态。塑性状态:
,则进入塑性状态。塑性状态: (https://www.xing528.com)
(https://www.xing528.com)
初始和后继屈服面:
正交流动法则:
状态检查:
如果F=0, ,则塑性加载状态;
,则塑性加载状态;
如果F=0,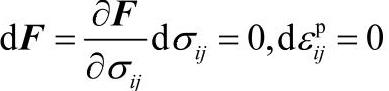 ,则塑性中性变载状态;
,则塑性中性变载状态;
如果F=0,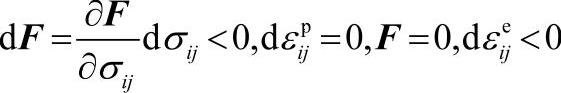 .则弹性卸载状态。
.则弹性卸载状态。
考虑成型过程的第n个时间步的求解过程。已知n时间步的位移、应变、应力分别为Un、εn、σn。设n+1时间步的位移、应变、应力分别为Un+1=Un+ΔUn+1、εn+1=εn+Δεn+1,、σn+1=σn+Δσn+1,采用N-R迭代法求解第n步到第n+1步的增量ΔUn+1。按式(4-19)得到第k迭代步增量ΔUk所满足的方程:
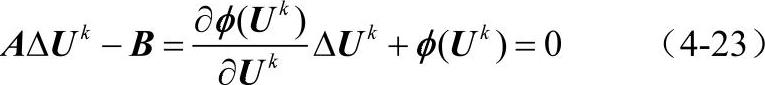
组合上述方程的总体刚度矩阵A和B矢量以后,通过迭代法求解AΔUk=B得到位移增量ΔUk,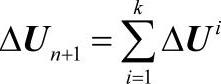 ,进一步求得Un+1,并据此进行收敛检查,如果收敛,则Un+1即下个时间步长的解。然后根据εn+1=εn+Δεn+1=εn+BΔUn+1求得n+1步的应变,根据σn+1=σn+Δσn+1=σ0+DepΔεn+1求得n+1步的应力。
,进一步求得Un+1,并据此进行收敛检查,如果收敛,则Un+1即下个时间步长的解。然后根据εn+1=εn+Δεn+1=εn+BΔUn+1求得n+1步的应变,根据σn+1=σn+Δσn+1=σ0+DepΔεn+1求得n+1步的应力。
2.使用刚塑性本构关系[97]刚塑性有限元法的理论基础是变分原理,它认为在所有动可容的速度场中,使泛函取得驻值的速度场是真实的速度场。因为这种方法忽略了弹性应变,但考虑了材料塑性变形体积不可压缩条件。与弹塑性有限元不同,对刚塑性变分原理离散后的方程在形式上虽然与式(4-18)相同,但是其未知量U不是节点位移而是节点速度。求解该方程需要给出非零的初始速度场。通过速度场可以计算出应变速率,通过速度、应变速率的时间积分可以得到节点位移和单元应变,利用流动法则可以获得偏应力,如果给出静水压力,还可以计算出应力场。这样刚塑性有限元避开了弹塑性有限元中由位移计算应变的几何非线性。
对于实体材料,刚塑性假设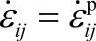 使得体积不可压缩
使得体积不可压缩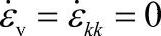 ,需要把这个约束条件加到变分方程中。对于疏松材料,塑性体积可压缩
,需要把这个约束条件加到变分方程中。对于疏松材料,塑性体积可压缩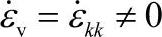 ,总变形能包括变形能和体积应变能:
,总变形能包括变形能和体积应变能: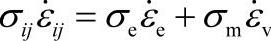 。对于实体材料,由于
。对于实体材料,由于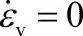 则相当于σm趋于无限大,这等效于用拉格朗日乘子法考虑塑性变形体积不可压缩约束,拉格朗日乘子λ=σm。如果假设静水压力σm单元内均匀,那么对于每个单元就多了一个未知量λ。当然这也就给出了不可压缩实体材料刚塑性处理时计算应力的一个方法。与弹塑性本构关系相比,在这种情况下的方程KU=F的未知量U添加了各单元的变量λ,刚度矩阵K和载荷向量F也添加了对应的项。将包括λ的方程KU=F改写为
则相当于σm趋于无限大,这等效于用拉格朗日乘子法考虑塑性变形体积不可压缩约束,拉格朗日乘子λ=σm。如果假设静水压力σm单元内均匀,那么对于每个单元就多了一个未知量λ。当然这也就给出了不可压缩实体材料刚塑性处理时计算应力的一个方法。与弹塑性本构关系相比,在这种情况下的方程KU=F的未知量U添加了各单元的变量λ,刚度矩阵K和载荷向量F也添加了对应的项。将包括λ的方程KU=F改写为
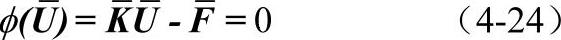
考虑成型过程的第n个时间步,已知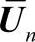 ,记
,记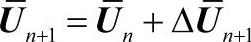 ,采用N-R迭代法求解第n步到第n+1步的增量
,采用N-R迭代法求解第n步到第n+1步的增量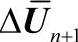 。按式(4-19)得到第k迭代步增量
。按式(4-19)得到第k迭代步增量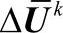 所满足的方程:
所满足的方程:
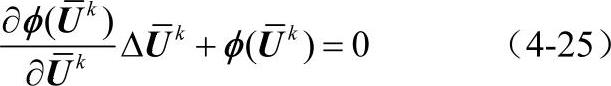
求解上述方程,得到第k+1步未知量值为: ,
,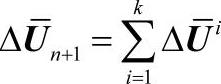 ,进一步求得
,进一步求得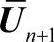 。据此进行收敛检查,如果收敛则
。据此进行收敛检查,如果收敛则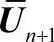 为下个时间步长的解,这就解出了n+1时间步的各节点速度和各单元的静水压力。根据节点速度可以计算出单元应变速率,利用时间积分,可以计算出节点位移、坐标和单元应变。根据应变速率,应变计算出单元偏应力,应用单元静水压力可计算出单元应力张量。如果用输入的应力、应变实验曲线替代等效应力与温度、应变速率、等效应变的函数表达式,那么可以通过对实验数据插值方法由温度、等效应变速率、等效应变计算出等效应力。
为下个时间步长的解,这就解出了n+1时间步的各节点速度和各单元的静水压力。根据节点速度可以计算出单元应变速率,利用时间积分,可以计算出节点位移、坐标和单元应变。根据应变速率,应变计算出单元偏应力,应用单元静水压力可计算出单元应力张量。如果用输入的应力、应变实验曲线替代等效应力与温度、应变速率、等效应变的函数表达式,那么可以通过对实验数据插值方法由温度、等效应变速率、等效应变计算出等效应力。
在有刚塑性限元分析中,通常设定了一个临界的应变速率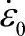 。其含义是:如果单元的
。其含义是:如果单元的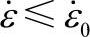 ,则
,则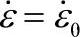 。实际上这是刚性区的判定标准。需要根据实际问题特征设置这个参数。设置过大或过小都会对计算结果有影响。例如进行超塑性成型分析时,如果该数值设置大于0.0001/s,那么几乎所有的超塑性单元都变成了刚性单元,从而使超塑成型分析失去了意义。
。实际上这是刚性区的判定标准。需要根据实际问题特征设置这个参数。设置过大或过小都会对计算结果有影响。例如进行超塑性成型分析时,如果该数值设置大于0.0001/s,那么几乎所有的超塑性单元都变成了刚性单元,从而使超塑成型分析失去了意义。
5.3.5 锻造工艺模拟中的热传导计算
1.变形与传热的双重迭代计算方法 因为塑性变形与热传导有耦合作用,目前的锻造工艺模拟软件对变形计算与传热计算采用两个迭代层次进行交叉耦合计算(见图4-55)。具体传热计算采用有限元空间离散和中心插值时间离散。在空间有限元离散方面塑性变形计算与传热计算采用相同的单元网格,在时间维方面两者采用相同的时间步长。变形计算按时间步长逐步加载,传热计算对时间维离散,分步计算温度变化速率。在锻造过程的第n个时间步长内,变形与传热耦合的每一个迭代步中,都是首先进行变形迭代计算,获得一个参考速度场以后,以此为基础进行n+1步的温度和温度变化率计算,按此温度返回变形计算修改刚度矩阵重新计算速度场,按新的速度场修改变形生热内容,再次计算温度和温度变化率,如此反复直到变形和温度迭代都收敛,获得n+1步的速度场和温度场。
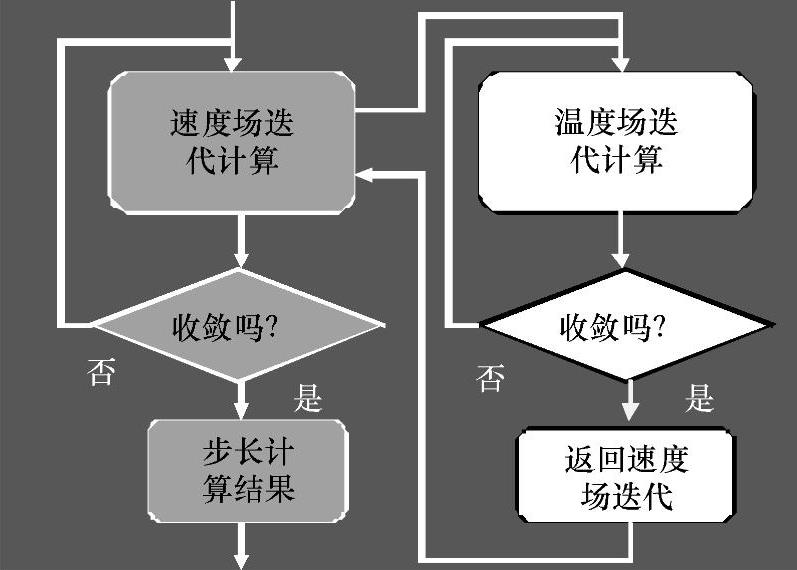
图4-55 速度场与温度场双重迭代算法
2.有限元空间离散与时间差分相结合的传热计算[99]对热传导方程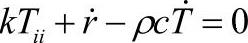 及其边值问题进行空间和时间离散,式中ρ是材料密度,c是材料比热容,k是材料的导热系数;r是物体内热源密度变化率。在热锻过程中,工件与模具接触传热,锻件自由表面与空气对流换热和热辐射,对称边界不传热。利用变分原理可以推导出热传导方程泛函表达式,对其进行空间离散。用T、
及其边值问题进行空间和时间离散,式中ρ是材料密度,c是材料比热容,k是材料的导热系数;r是物体内热源密度变化率。在热锻过程中,工件与模具接触传热,锻件自由表面与空气对流换热和热辐射,对称边界不传热。利用变分原理可以推导出热传导方程泛函表达式,对其进行空间离散。用T、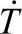 分别表示整个物体全部节点的温度向量和温度变化率向量,则热传导边值问题有限元离散化后的矩阵方程为
分别表示整个物体全部节点的温度向量和温度变化率向量,则热传导边值问题有限元离散化后的矩阵方程为

式中 K——整体热传导矩阵;
C——整体热容矩阵。
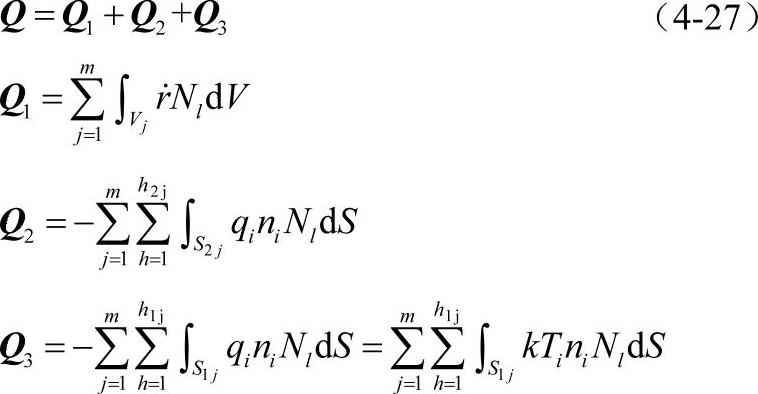
Q1+Q2为整个物体通过体积热源、外边界与外界进行的热交换向量,Q3是在物体内边界上出现的热流矢量[99],对于简单的C0型单元,边界温度导数在边界不连续并使Q3≠0,这与实际情况不符,会造成预测的温度振荡,通常使用集中热容矩阵防止这种情况[99]。如果使用C1型单元可保证温度导数在单元边界上连续,使Q3=0。
5.3.6 算例
(1)GH4133B涡轮盘模锻工艺。图4-56所示是一个GH4133B涡轮盘模锻工艺的数值模拟算例,使用二维轴对称模块,图中所示的只是模拟结果的局部放大。图4-56a显示模具设计不当出现工件折叠的缺陷;图4-56b显示修改了模具形状以后避免了折叠缺陷;图4-56c显示坯料过大引起了锻件飞边附近的温升太快出现了过烧缺陷;图4-56d显示减小坯料体积后高温过烧缺陷消失[100]。
(2)大型钢锭JTS压实连砧工艺数值模拟[125]。图4-57所示为某大钢锭4趟JTS连砧压实翻转过程静水压力与空洞闭合的模拟结果,翻转顺序为0°、180°、90°、180°。轴向中心孔直径为330mm,为钢锭外径的10%。可以看出,每一趟压实都对空洞闭合起正面促进作用。它们的共同特点是靠近水口端中心盲孔的闭合率总是高于钳口端,这是因为每趟锻打顺序都是由钳口向水口。前面锻打会对后面的空洞闭合有贡献,这说明连砧锻打的方向影响空洞闭合率。另外,锻打时工件上表面出现拉应力,即静水压力>0。
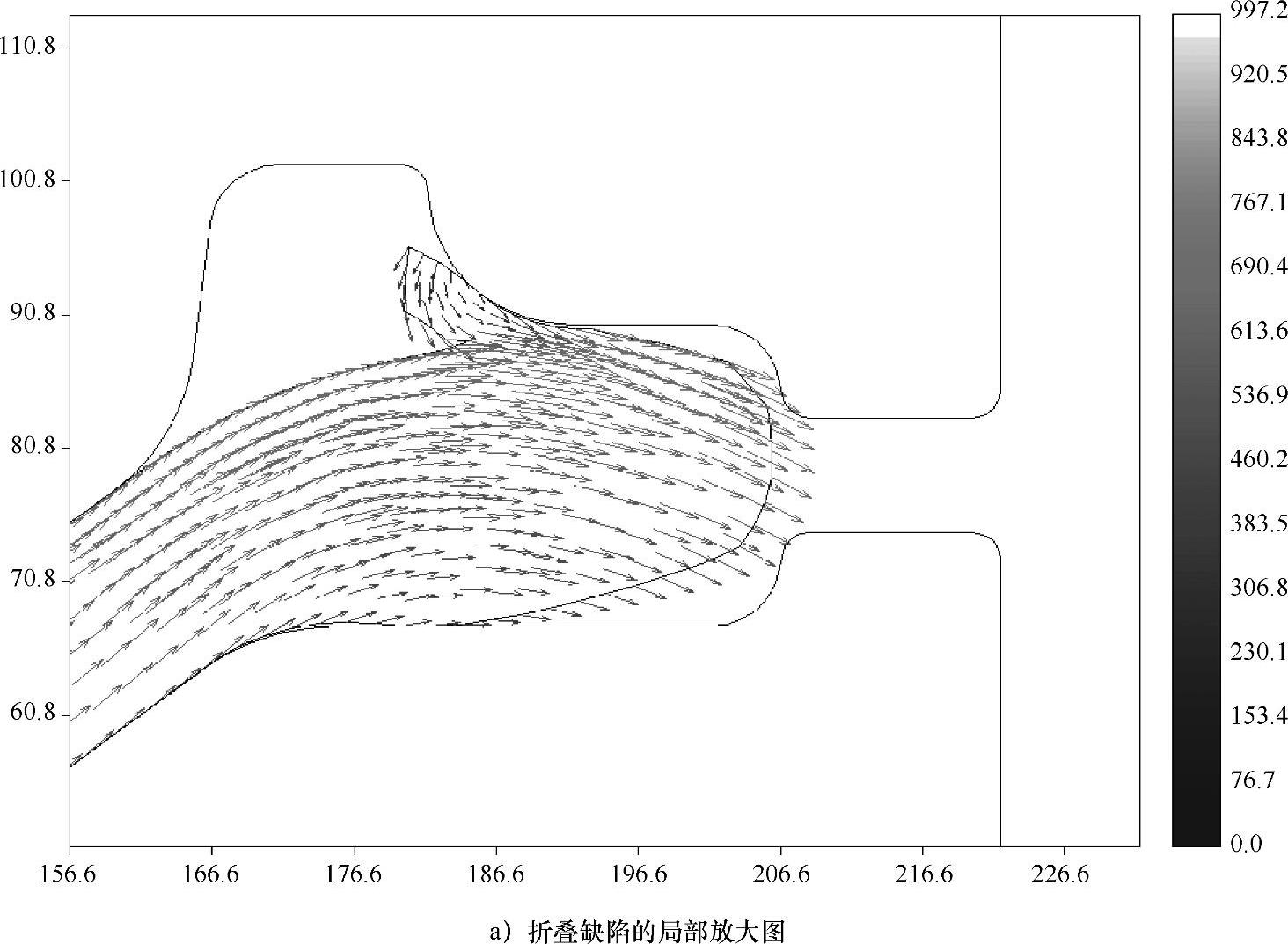
图4-56 涡轮盘模锻数值模拟结果局部图[100]
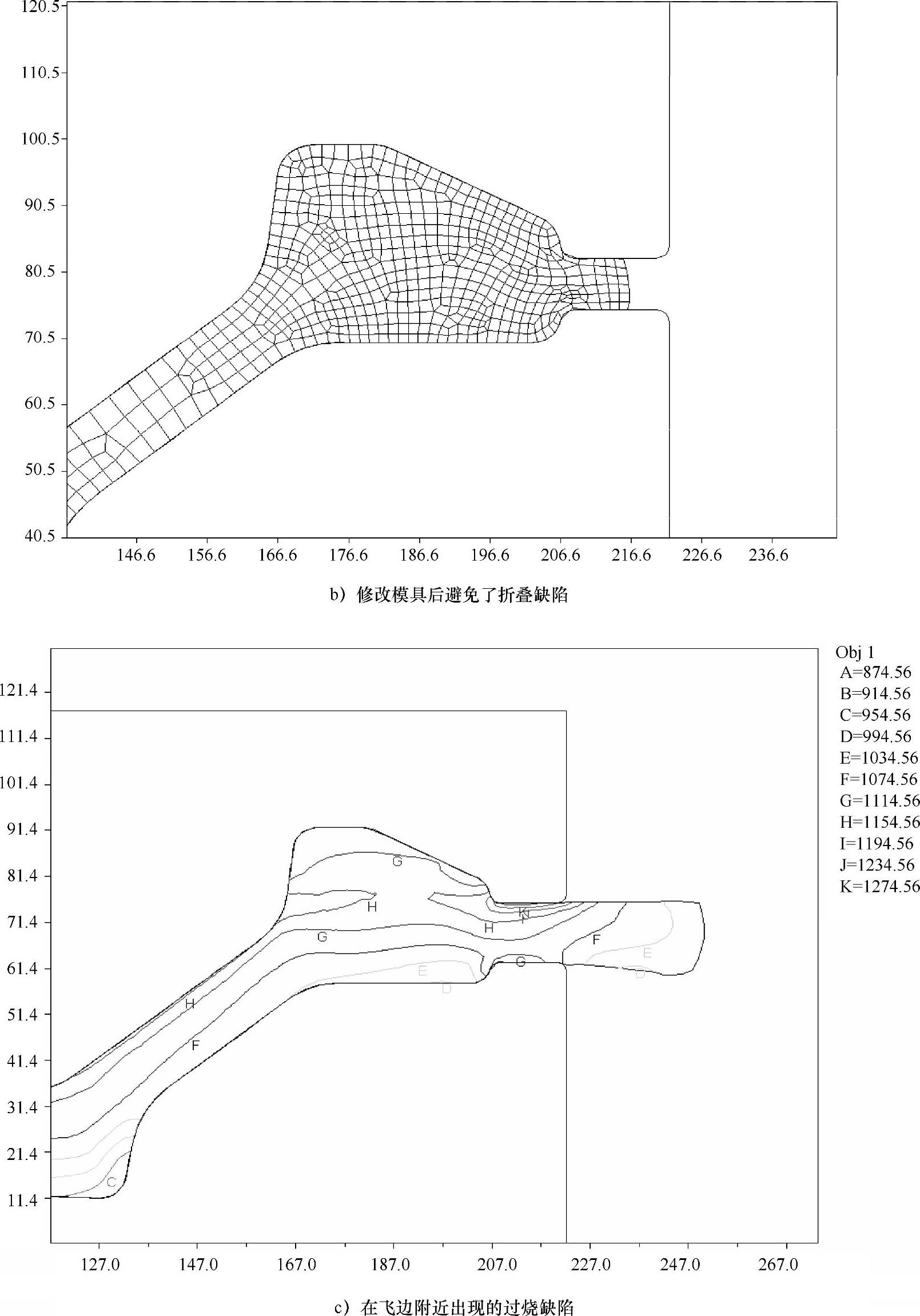
图4-56 涡轮盘模锻数值模拟结果局部图[100](续)

图4-56 轮盘模锻数值模拟结果局部图[100](续)
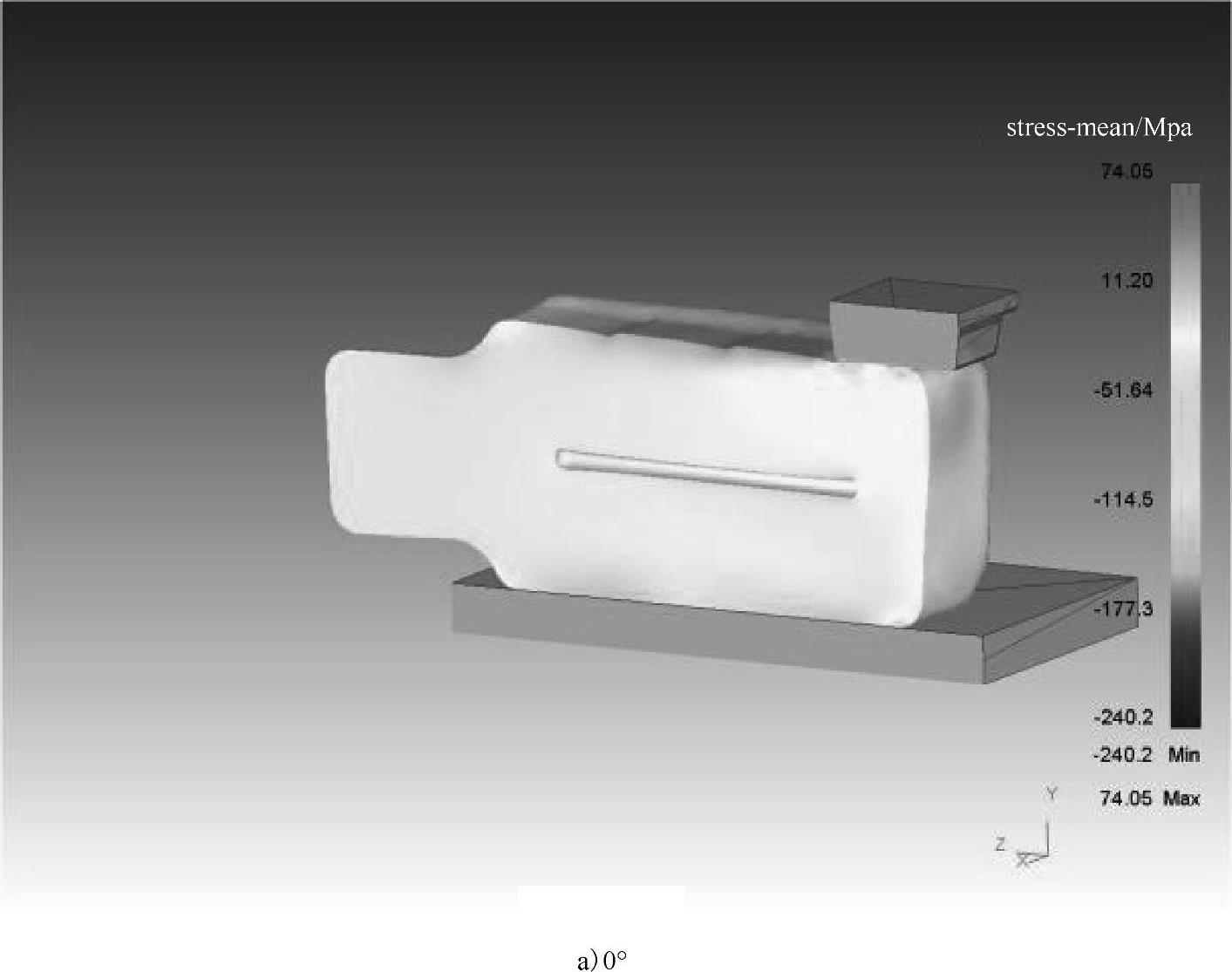
图4-57 某大钢锭4趟J TS连砧压实翻转过程静水压力与空洞闭合的模拟结果[125]
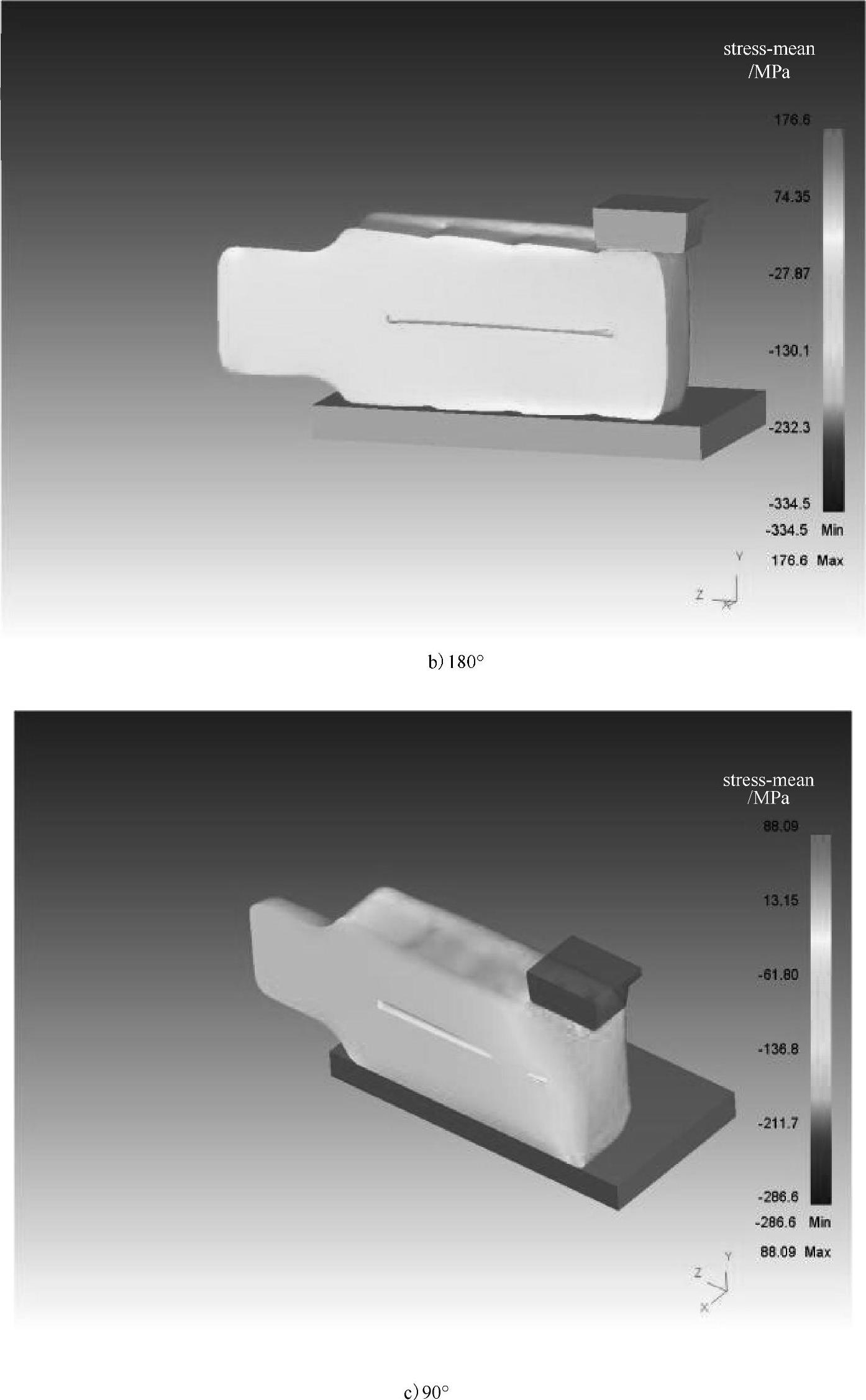
图4-57 某大钢锭4趟J TS连砧压实翻转过程静水压力与空洞闭合的模拟结果[125](续)
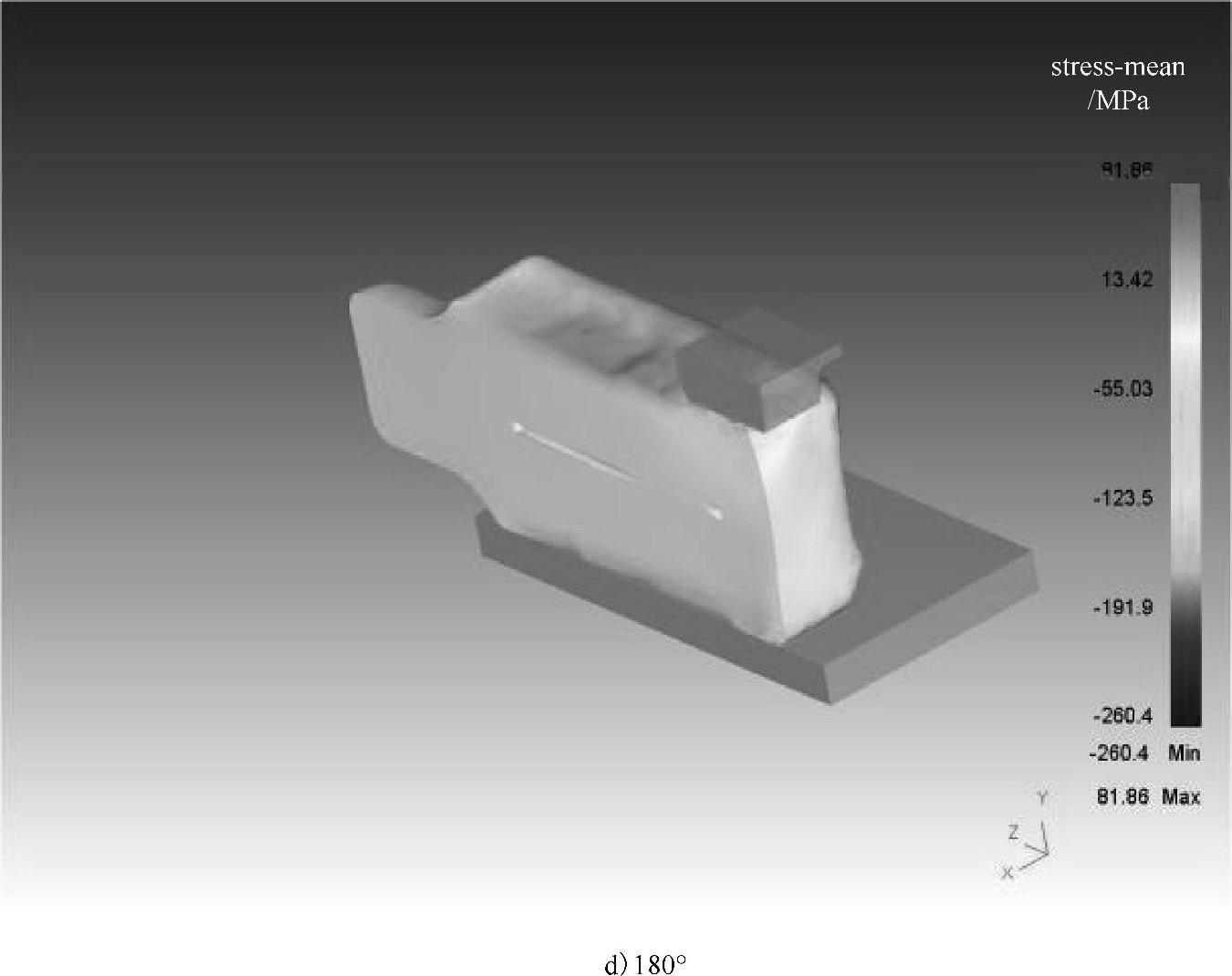
图4-57 某大钢锭4趟J TS连砧压实翻转过程静水压力与空洞闭合的模拟结果[125](续)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




