揭秘新古典增长模型：技术进步对经济稳态的影响

生产函数在本质上是从静态的角度分析经济增长的直接原因，但由于不同时期的经济增长会呈现出不同的特征，故需要对经济增长进行动态分析。20世纪50年代后期的新古典增长理论是较为有影响力的理论之一，该理论将注意力集中在资本积累以及它与储蓄决策的联系等方面。

1.基本假定

新古典增长模型，又称索洛增长模型，是建立在一个新古典生产方程体系之上，强调了在一个封闭的没有政府部门的经济中储蓄、人口增长及技术进步对经济增长的作用，它关注的焦点是资本积累以及它与储蓄决策等的联系方面。新古典增长模型的基本假定是：

（1）经济由一个部门组成，该部门生产一种既可用于投资也可用于消费的商品；

（2）该经济为不存在国际贸易的封闭经济，且政府部门被忽略；

（3）生产的规模报酬不变；

（4）该经济的技术进步、人口增长及资本折旧的速度都由外生因素决定；

（5）社会储蓄函数为S=sY，s为储蓄率。

2.没有技术进步下的新古典增长模型

首先我们来考虑没有技术进步下的新古典增长模型。在增长核算中，我们已经推导出了公式（16.3），由于没有技术进步，故得：

用y表示人均产量，即y=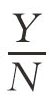，k表示人均资本，即k=，可知y取决于k，则生产函数可表示为下述人均形式：

一般来说，资本积累受到投资与折旧的影响。假定折旧率是一个固定值δ（0＜δ＜1），人口增长率为n，且储蓄能有效地转化为投资，则有：

上式两边同除以N，可得：

此外，由k=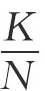，对该式关于时间变量求导，利用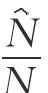=n经运算可得：

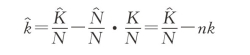
进而有：

将上式带入（16.7）式中，整理可得：

公式（16.8）是新古典增长模型的基本方程。这一关系式表明人均资本变化等于人均储蓄减去（n+δ）k项。表达式（n+δ）k可以理解为必要的投资，它是保持人均资本k不变的必要投资。为了阻止人均资本k下降，需要用一部分投资来抵消折旧，这部分投资就是δk。同样还需要一些投资，因为劳动数量以n的速率在增长，这部分投资就是nk项。因此资本存量必须以（n+δ）的速度增长，以维持k不变。总计为（n+δ）k的储蓄（或投资）被称为资本的广化。当人均储蓄大于临界投资所必要的数量时，k将上升，这时经济社会经历着资本深化^[1]。根据以上解释，新古典增长模型的基本方程可表述为：

资本深化=人均储蓄（投资）-资本广化

3.具有技术进步的新古典增长模型

首先，我们构建具有技术进步的新古典增长模型，为此把经济的生产函数写为：

在式中，AN被称为有效劳动，在这种情况下，新古典增长理论对生产函数的假定就变为，产出Y是资本K和有效劳动AN的一次齐次函数。

记，称其为按有效劳动平均的产量，称其为按有效劳动平均的资本，则公式（16.9）可写为：

新古典经济增长模型的一个重要基本假定是，技术进步是外生给定的，即假定变量A以一个固定比例α增长，即有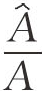=a。(www.xing528.com)

通过对方程关于时间变量t求导数可得：

进一步地，利用和式（16.10）、（16.11）可得：

式（16.12）便是具有技术进步的新古典增长模型的基本方程。这一方程表明，每单位有效劳动的资本存量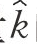的变化取决于以下两个方面：等式右边第一项sf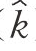（）表示每单位有效劳动的实际投资量；第二项（n+δ+a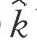）可以理解为投资平衡水平，表示投资量必须恰好使每单位有效劳动的投资保持在现有水平。

4.稳态及其条件

在有关增长文献中，稳态是指包括资本存量和产出在内的有关内生变量将不会随时间的推移而变化的一种状态。根据上述说明，在新古典增长模型中，经济达到稳态的条件是k=0。对没有技术进步的新古典增长模型来说，该模型稳态的条件是：

对具有技术进步的新古典增长模型来说，该模型稳态的条件是：

如果用图形表示，我们以没有技术进步的新古典增长模型为例进行说明，如图16-2所示。

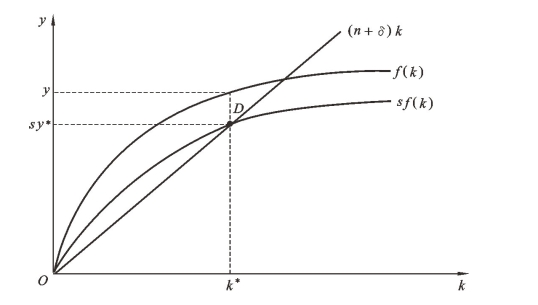
图16-2　新古典增长模型的稳态

根据上述稳态的定义，在图16-2中，当经济在D点上运行时，对应的人均资本存量为k*。当k为k*时，sf（k）曲线正好与（n+δ）k相交，这意味着两者相等。而由方程（16-8）可知，此时有k=0，即这时的人均资本量将不随着时间的推移而变化。所以图中D点所对应的状态即为该模型的稳态。

5.稳态时的增长率

当经济达到稳态时，新古典增长模型中的相关内生变量的增长率有何变化呢？我们首先来考虑没有技术进步的新古典增长模型。

根据图16-2，我们知道经济的稳态出现在D点，对于D点，求得人均资本k、人均产量y和人均储蓄（投资）的稳态值分别为k*、y*和sy*。

由于k*和y*都为常数，可知它们的增长率均为零，即

gk=gy=0

上式说明了新古典增长模型中的一个非常重要的结论，即人均资本和人均产出的稳态增长率均为零。出于这个原因，可以说在没有技术进步的情况下，新古典增长模型并没有对长期人均增长的决定因素做出解释。

进一步地，由于和，以及人口增长率为n，我们可以得出

gK=gY=n

我们将上述结论归纳得出表16-2。

表16-2　无技术进步下的稳态增长率

对于具有技术进步的新古典增长模型的稳态增长率（见表16-3），我们直接给出结论，有兴趣的同学可以参考上文进行推导。

表16-3　在技术进步下的稳态增长率

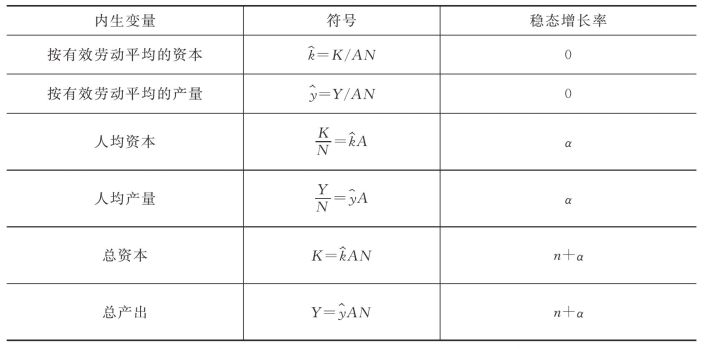
在加入技术进步因素后，新古典增长模型可以解释本章前面所展示的生活水平的持续提高。也就是说，技术进步会导致人均产出的持续增长。一旦经济达到稳态，人均产出的增长率就只取决于技术进步的速率。

综上所述，新古典增长理论的主要贡献是什么？它改变了我们关于增长过程和公共政策的思维方式。如果技术水平不同是导致各国生活水平差异的主要原因，且假定技术是一个可以生产出来的要素，那么关于经济增长的政策就应该着重关注国家怎样才能提高技术水平。

在投入既定的条件下，技术变革能够使产出增加，因而它是国民经济增长的关键因素。新增长理论试图揭示产生技术变革的过程。这种理论强调技术变革是一种容易引起严重的市场不灵的产出。因为技术是一种公共品，它的生产成本昂贵但复制成本却很低廉。政府正在不断地加大力度来保护那些开发新技术的人或企业的知识产权。