需求弹性：影响价格的关键因素

需求方面的弹性主要包括需求的价格弹性、需求的交叉价格弹性和需求的收入弹性。其中，需求的价格弹性又被简称为需求弹性。下面将重点考察需求的价格弹性。

1.什么是需求价格弹性？

需求的价格弹性表示在一定时期内一种商品的需求量变动对该商品的价格变动的反应程度。或者说，它表示在一定时期内一种商品的价格变化百分之一时所引起的该商品的需求量变化的百分比。其公式为：

2.什么是弧弹性？什么是点弹性？

需求的价格弹性分为弧弹性和点弹性。

需求的价格弧弹性表示某商品需求曲线上两点之间的需求量的变动对价格的变动的反应程度。简单地说，它表示需求曲线上两点之间的弹性。

假定需求函数为Q=f（P），ΔQ和ΔP分别表示需求量的变动量和价格的变动量，以ed表示需求的价格弹性系数，则需求的价格弧弹性公式为：

在通常情况下，由于商品的需求量和价格是呈反方向变动的，即ΔQ/ΔP为负值，所以，为了便于比较，就在式（2.3）和式（2.4）中均加了一个负号，以使需求的价格弹性系数取正值。当需求曲线上两点之间的变化量趋于无穷小时，需求的价格弹性要用点弹性来表示。也就是说，它表示需求曲线上某一点的需求量变动对价格变动的反应程度。在式（2.4）的基础上，需求的价格点弹性的公式为：

比较式（2.4）和式（2.5）可见，需求的价格弧弹性和点弹性的本质是相同的。它们的区别仅在于：前者表示需求曲线上两点之间价格变动时的弹性，而后者表示在需求曲线的某一点上价格变动量无穷小时的弹性。

1）如何计算弧弹性？

图2-14为需求函数的几何图形。

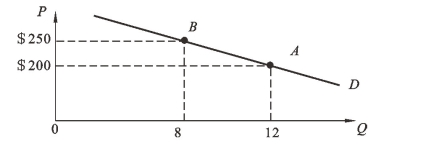
图2-14　需求函数的几何图形

图中需求曲线上A、B两点的价格分别为200美元和250美元，相应的需求量分别为12和8。当商品的价格由200美元上升为250美元时，或者当商品的价格由250美元下降为200美元时，应该如何计算相应的弧弹性值呢？根据（2.4）式，相应的弧弹性分别计算如下。

从A到B：价格上升（250-200）/200=25%；数量下降（8-12）/12=-33%

弹性=-（-33%）/25%=1.33

从B到A：价格下降20%，数量上升50%，弹性=50%/20%=2.50

显然，由A点到B点和由B点到A点的弧弹性系数值是不相同的。其原因在于：尽管在上面两个计算中，ΔQ和ΔP的绝对值都相等，但由于P和Q所取的基数值不相同，所以，两种计算结果便不相同。这样一来，在需求曲线的同一条弧上，涨价和降价产生的需求的价格弹性系数值便不相等。所以，要根据涨价和降价的具体情况，来求得不同的ed值。但是，如果仅仅是一般地计算需求曲线上某一段的需求价格弧弹性，而不是具体地强调这种需求的价格弧弹性是作为涨价还是降价的结果，一般采用中点法来计算。

根据中点公式（2.7），上例中A、B两点间的需求的价格弧弹性为：

由此可见，需求的价格弧弹性的计算可以有三种情况，它们分别是涨价时计算的ed、降价时计算的ed，以及按中点公式计算的ed。至于到底应该采用哪一种计算方法，需要视具体情况和需要而定。

2）弧弹性有哪些类型？

我们已经知道，需求的价格弹性是告诉我们，当商品的价格变动1%时，需求量的变动究竟有多大的百分比。于是，我们完全可以设想：在商品的价格变化1%的前提下，需求量的变化率可能大于1%，这时有ed＞1；需求量的变化率也可能小于1%，这时有ed＜1；需求量的变化率也可能恰好等于1%，这时有ed=1。进一步讲，由于ed＞1表示需求量的变动率大于价格的变动率，即需求量对于价格变动的反应是比较敏感的，所以，ed＞1被称为富有弹性。由于ed＜1表示需求量的变动率小于价格的变动率，即需求量对于价格变动的反应欠敏感，所以，ed＜1被称为缺乏弹性。ed=1是一种巧合的情况，它表示需求量和价格的变动率刚好相等，ed=1被称为单一弹性或单位弹性。以上这三种类型的需求的价格弧弹性分别如图2-15（a）、图2-15（b）和图2-15（c）所示。

比较图2-15（a）和图2-15（b）可以看出，就需求的价格弧弹性而言，富有弹性的需求曲线相对比较平坦，缺乏弹性的需求曲线相对比较陡峭。但是，特别需要引起注意的是，尽管在经济学中，把富有弹性的需求绘制成一条相对平坦的曲线和把缺乏弹性的需求绘制成一条相对陡峭的曲线已成为一种习惯，但是，在有些场合，这种绘制方法便会成为一种不好的甚至错误的方法。譬如，在图2-15（a）中，横轴上每0.5厘米的刻度由10、20、30、40、50改为11、12、13、14、15以后，平坦的需求曲线就是缺乏弹性的了。所以在使用这种绘制方法时必须十分小心。关于这一点，在以后分析需求曲线的斜率和需求的价格点弹性的关系时，会得到进一步的说明。

再看图2-15（d）和图2-15（e）。图2-15（d）中需求曲线为一条水平线。水平的需求曲线表示在既定的价格水平（如图中的P=3），需求量是无限的。从需求的价格弹性的角度看，对于水平的需求曲线来说，只要价格有一个微小的上升，就会使无穷大的需求量一下子减少为零。也就是说，相对于无穷小的价格变化率，需求量的变化率是无穷大的，即有ed=∞，这种情况被称为完全弹性。

图2-15（e）中的需求曲线是一条垂直线。垂直的需求曲线表示相对于任何价格水平需求量都是固定不变的（如图中总是有Q=30）。从需求的价格弹性的角度看，对于垂直的需求曲线来说，无论价格如何变化，需求量的变化量总是为零，即有ed=0，这种情况被称为完全无弹性。(www.xing528.com)

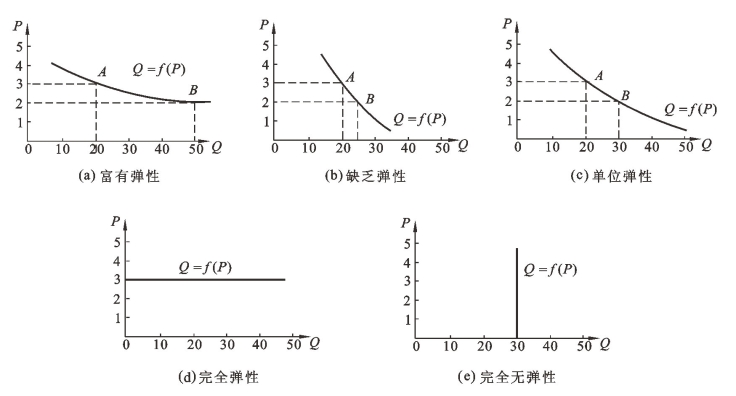
图2-15　需求的价格弧弹性的五种类型

利用图2-15以弧弹性为例分析的需求弹性的五种情况，是区分需求弹性大小的五种基本类型。在需求的价格点弹性的事例中，这五种基本类型也同样存在，下面的分析会说明这一点。最后需要指出，这五种基本类型也适用于其他任何一个具体的弹性概念。

3）什么是点弹性？

需求的价格点弹性的计算可以利用需求的价格点弹性的定义公式即（2.5）式，来计算给定的需求曲线上某一点的弹性。以需求函数Qd=2400-400P来说明这一计算方法。根据（2.5）式，由需求函数Qd=2400-400P可得：

ed=-dQ/dP·P/Q=-（-400）·P/Q=400·P/Q

在图2-16需求曲线上的a点，当P=5时，由需求函数可得Qd=2400-400×5=400，即相应的价格-需求量组合为（5，400）。将其代入上式，便可得ed=400·P/Q=400×（5/400）=5，即图2-16需求曲线上a点的需求的价格弹性值为5。

同样地，在图2-16需求曲线上的b点，当P=4时，由需求函数可得Qd=2400-400×4=800，即相应的价格-需求量组合为（4，800），于是有：ed=400·P/Q=400×（4/800）=2，即图2-16中需求曲线上b点的需求的价格弹性值为2。

图2-16　需求函数Qd=2400-400P的几何图形

注意区分需求曲线的斜率和需求价格弹性两个概念，二者紧密相联但又不同。

需求曲线某一点的斜率为dP/dQ，而需求的价格点弹性不仅取决于该点的斜率的倒数值dQ/dP，还取决于相应的价格与需求量的比值P/Q。线性需求曲线上每点的斜率都相等，但每点的点弹性值都不相等。一般地，需求价格弹性越大，曲线的斜率就越平坦；需求价格弹性越小，曲线的斜率就越陡峭。由此可见，直接把需求曲线的斜率和需求的价格弹性等同起来是错误的。严格区分这两个概念，不仅对于线性需求曲线的点弹性来说，而且对于任何形状的需求曲线的弧弹性和点弹性来说，都是必要的。

3.影响需求价格弹性的因素有哪些？

影响需求的价格弹性的因素有很多，其中主要有以下几个。

第一，商品的可替代性。一般说来，一种商品的可替代品越多，相近程度越高，则该商品的需求的价格弹性往往就越大；相反，该商品的需求的价格弹性往往就越小。例如，在苹果市场，当国光苹果的价格上升时，消费者就会减少对国光苹果的需求量，增加对相近的替代品如香蕉苹果的购买。这样，国光苹果的需求弹性就比较大。又如，对于食盐来说，没有很好的可替代品，加之食盐又是生活必需品，所以，食盐价格的变化所引起的需求量的变化几乎等于零，它的需求的价格弹性是极其微小的。对一种商品所下的定义越明确、越狭窄，这种商品的相近的替代品往往就越多，需求的价格弹性也就越大。譬如，某种特定商标的豆沙馅面包的需求要比一般的甜馅面包的需求更有弹性，甜馅面包的需求又比一般的面包的需求更有弹性，而面包的需求的价格弹性比一般的面粉制品的需求的价格弹性又要大得多。

第二，商品用途的广泛性。一般说来，一种商品的用途越广泛，它的需求的价格弹性就可能越大；相反，用途越是狭窄，它的需求的价格弹性就可能越小。这是因为，如果一种商品具有多种用途，当它的价格较高时，消费者只购买较少的数量用于最重要的用途上；当它的价格逐步下降时，消费者的购买量就会逐渐增加，将商品越来越多地用于其他的各种用途上。

第三，商品对消费者生活的重要程度。一般说来，生活必需品的需求的价格弹性较小，非必需品的需求的价格弹性较大。例如，面粉的需求的价格弹性较小，电影票的需求的价格弹性较大。

第四，商品的消费支出在消费者预算总支出中所占的比重。消费者在某商品上的消费支出在预算总支出中所占的比重越大，该商品的需求的价格弹性可能就越大；反之，则越小。例如，火柴、盐、铅笔、肥皂等商品的需求的价格弹性就是比较小的。这是因为，消费者每月在这些商品上的支出是很小的，消费者往往不太重视这类商品价格的变化。

第五，所考察的消费者调节需求量的时间。一般说来，所考察的调节时间越长，则需求的价格弹性可能就越大。这是因为，在消费者决定减少或停止对价格上升的某种商品的购买之前，他一般需要花费时间去寻找和了解该商品的替代品。例如，当石油价格上升时，消费者在短期内通常不会较大幅度地减少石油需求量。但设想在长期内，消费者可能找到替代品，于是，石油价格上升会导致石油的需求量较大幅度地下降。

需要指出，一种商品需求的价格弹性的大小是各种影响因素综合作用的结果，所以在分析一种商品的需求的价格弹性的大小时，要根据具体情况进行全面的综合分析。

4.需求的价格弹性和厂商的销售收入

在实际的经济生活中会发生这样一些现象：有的厂商提高自己的产品价格，能使自己的销售收入得到提高，而有的厂商提高自己的产品价格，却反而使自己的销售收入降低了。这意味着，以降价促销来增加销售收入的做法，对有的产品适用，对有的产品却不适用。如何解释这些现象呢？这便涉及商品的需求的价格弹性的大小和厂商的销售收入两者之间的相互关系。

我们知道，厂商的销售收入等于商品的价格乘以商品的销售量。在此假定厂商的商品销售量等于市场上对其商品的需求量。这样，厂商的销售收入就又可以表示为商品的价格乘以商品的需求量，即厂商销售收入=P·Q，其中，P表示商品的价格，Q表示商品的销售量即需求量。前面已经讲过，商品的需求的价格弹性表示商品需求量的变化率对商品价格的变化率的反应程度。这意味着，当一种商品的价格P发生变化时，这种商品需求量Q的变化情况，进而提供这种商品的厂商的销售收入P·Q的变化情况，将必然取决于该商品的需求的价格弹性的大小。所以，在商品的需求价格弹性和提供该商品的厂商的销售收入之间存在着密切的关系，这种关系可归纳为以下三种情况（见图2-17）。

第一种情况：对于ed＞1的富有弹性的商品，降低价格会增加厂商的销售收入；相反，提高价格会减少厂商的销售收入，即厂商的销售收入与商品的价格呈反方向变动。这是因为，当ed＞1时，厂商降价所引起的需求量的增加率大于价格的下降率，这意味着价格下降所造成的销售收入的减少量必定小于需求量增加所带来的销售收入的增加量，所以，降价最终带来的销售收入P·Q值是增加的。相反，在厂商提价时，最终带来的销售收入P·Q值是减少的。这种情况如图2-17（a）所示。

图2-17　需求弹性与销售收入

图2-17（a）中需求曲线上a、b两点之间的需求是富有弹性的，两点之间的价格变动率引起一个较大的需求量的变动率。具体地看，当价格为P1，需求量为Q1时，销售收入P1·Q2相当于矩形OP1aQ1的面积；当价格为P2，需求量为Q2时，销售收入P2·Q2相当于矩形OP2bQ2的面积。显然，前者面积小于后者面积。这就是说，若厂商从a点运动到b点，则降价会使销售收入增加；若从b点运动到a点，则提价会使销售收入减少。可以具体举例说明这种情况。假设某商品的ed=2。开始时，商品的价格为10元，需求量是100，厂商的销售收入=10×100=1000（元）。当商品的价格上升1%，即价格为10.10元时，由于ed=2，所以，相应的需求量的下降率为2%，即需求量下降为98，厂商的销售收入=10.10×98=989.80元。显然，厂商提价后的销售收入反而下降了。

第二种情况：对于ed＜1的缺乏弹性的商品，降低价格会使厂商的销售收入减少；相反，提高价格会使厂商的销售收入增加，即销售收入与商品的价格呈同方向变动。其原因在于：当ed＜1时，厂商降价所引起的需求量的增加率小于价格的下降率。这意味着需求量增加所带来的销售收入的增加量并不能全部抵消价格下降所造成的销售收入的减少量。所以，降价最终使销售收入P·Q值减少。相反，在厂商提价时，最终带来的销售收入P·Q值增加。用图2-17（b）来说明这种情况。图中需求曲线上a、b两点之间的需求是缺乏弹性的，两点之间的价格变动率引起一个较小的需求量的变动率。价格分别为P1和P2时，销售收入分别为矩形OP1aQ1的面积和矩形OP2bQ2的面积，且前者面积大于后者面积。这就是说，当厂商降价，即由a点运动到b点时，销售收入是减少的；相反，当厂商提价，即由b点运动到a点时，销售收入是增加的。

第三种情况：对于ed=1的具有单位弹性的商品，降低价格或提高价格对厂商的销售收入都没有影响。这是因为，当ed=1时，厂商变动价格所引起的需求量的变动率和价格的变动率是相等的。这样一来，由价格变动所造成的销售收入的增加量或减少量刚好等于由需求量变动所带来的销售收入的减少量或增加量，所以，无论厂商是降价还是提价，销售收入P·Q值都是固定不变的，如图2-17（c）所示。图中需求曲线上a、b两点之间的需求弹性为单位弹性。价格为P1时的销售收入即矩形OP1aQ1的面积等于价格为P2时的销售收入即矩形OP2bQ2的面积。显然，不管厂商是因降价由a点运动到b点，还是因提价由b点运动到a点，其销售收入量都是不变的。读者可以自己举出具体数字例子，分别说明第二种和第三种情况。以上三种情况都是以需求的弧弹性为例进行分析的。

与以上三种情况相对应，在西方经济学中，也可以根据商品的价格变化所引起的厂商的销售收入的变化，来判断商品的需求的价格弹性的大小。如果某商品价格变化引起厂商销售收入反方向变化，则该商品是富有弹性的；如果某商品价格变化引起厂商销售收入同方向变化，则该商品是缺乏弹性的；如果厂商的销售收入不随商品价格的变化而变化，则该商品具有单位弹性。