层次分析法：构建问题层次结构图的细节分析及一致性检验

层次分析法（analytic hierarchy process，AHP 法）是美国运筹学家沙旦（T.L.Saaty）于20 世纪70 年代提出的，是一种定性与定量分析相结合的多目标决策分析方法。特别是将决策者的经验判断给予量化，对目标（因素）结构复杂且缺乏必要的数据情况下更为实用，所以，近几年来此法在我国的实际应用中发展较快。

1.AHP 法原理

例如，某工厂在扩大企业自主权后，有一笔企业留成的利润，这时厂领导要合理使用这笔资金。根据各方面的反映和意见，提出可供领导决策的方案有：（1）作为奖金发给职工；（2）扩建职工食堂、托儿所；（3）开办职工业余技术学校和培训班；（4）建立图书馆；（5）引进新技术扩大生产规模等。领导在决策时，要考虑到调动职工的劳动生产积极性，提高职工的文化技术水平，改善职工的物质文化生活状况等方面，故需对这些方案的优劣性进行评价，排队后，才能做出决策。

面对这类复杂的决策问题，处理的方法是：先对问题所涉及的因素进行分类，然后构造一个各因素之间相互联结的层次结构模型。因素分类为：一为目标类，如合理使用今年企业留利××万元，以促进企业发展；二为准则类，这是衡量目标能否实现的标准，如调动职工的劳动积极性，提高企业的生产技术水平；三为措施类，是指实现目标的方案、方法、手段等，如发奖金、扩建集体福利设施、引进新技术，等等。按目标到措施的自上而下地将各类因素之间的直接影响关系排列于不同层次，构成一层次结构图，如图11-15 所示。

图11-15　层次结构图

构造好各类问题的层次结构图是一项细致的分析工作，要有一定的经验。根据层次结构图确定每一层的各因素的相对重要性的权数，直至计算出措施层中各方案的相对权数。这就给出了各方案的优劣次序，以便供领导决策。此方法的原理是这样的。

设有n 件物体 A1，A2，…，An，它们的质量分别为w1，w2，…，wn，若将其质量两两比较，其比值可构成n×n 矩阵A：

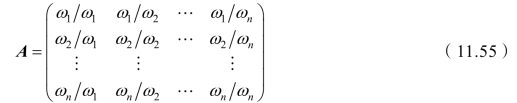
A 矩阵具有如下性质：

若用质量向量

右乘A 矩阵，可得到如下矩阵：

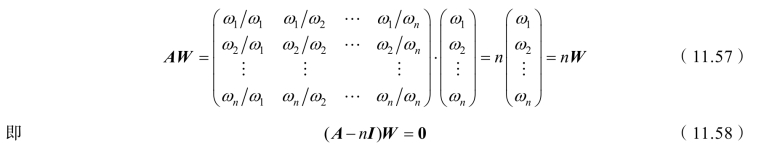
由矩阵理论可知，W 为特征向量，n 为特征值。若W 未知时，可根据决策者对物体之间的两两相比的关系，从主观上做出比值的判断，或用Delphi 法来确定这些比值，使A 矩阵为已知，并将判断矩阵记作

根据正矩阵的理论，可以证明：若A 矩阵有以下特点（设aij＝wi/wj）：

则该矩阵具有唯一非零的最大特征值λmax，且λmax＝n。

若给出的判断矩阵具有上述特征，则该矩阵具有完全一致性。然而人们对复杂事物的各因素，采用两两比较时，不可能做到判断的完全一致性，而存在估计误差，这必然导致特征值及特征向量也有偏差。这时问题由AW＝nW 变成这里λmax是矩阵的最大特征值，W ′是带有偏差的相对权重向量。这就是由判断不相容而引起的误差。为了避免误差太大，要衡量矩阵的一致性，当A 矩阵完全一致时，因aii＝1，则

即存在唯一的非零λ＝λmax＝n。而当矩阵存在判别不一致时，一般是λmax≥n，这时

则以其平均值作为检验判断矩阵的一致性指标（CI）：

因此，当λmax＝n，CI＝0 时，为完全一致；CI值越大，判断矩阵的完全一致性越差。一般只要CI≤0.1，即可认为判断矩阵的一致性可以接受，否则重新进行两两比较判断。

判断矩阵的维数n 越大，判断的一致性将越差，故应放宽对高维判断矩阵一致性的要求。于是引入修正值RI，如表11-24 所示，并取更为合理的CR 为衡量判断矩阵一致性的指标：

表11-24

2.标度

为了使各因素之间进行两两比较得到量化的判断矩阵，引入1～9的标度。根据心理学家的研究提出：人们区分信息等级的极限能力为7±2，特制订表11-25。因为自己与自己比是同等重要的，因此对角线上元素不用做判断比较，只需给出矩阵对角线上三角形中的元素。可见，n×n 矩阵中，只需要给出个判断数值。

表11-25

除表11-25的标度方法以外，还可以用其他标度方法。(www.xing528.com)

3.层次模型

根据具体问题，一般分为目标层、准则层和措施层（见图11-16），复杂的问题可分为总目标层、子目标层、准则层（或制约因素层）、方案措施层，或分为层次更多的结构（见图11-17）。下面举若干例子加以说明。

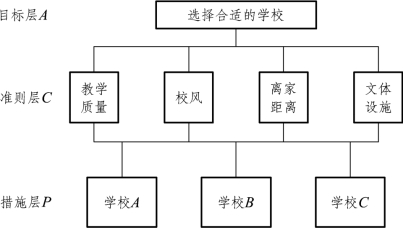
图11-16

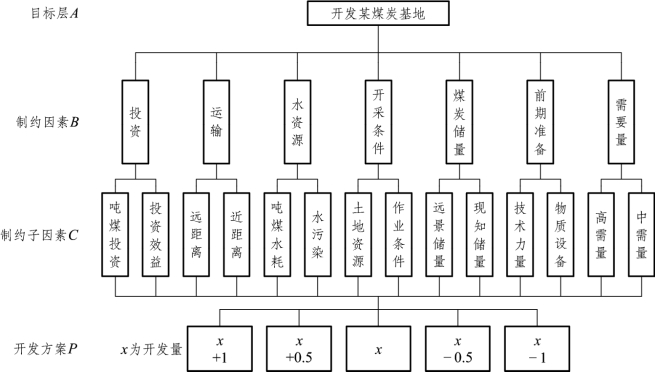
图11-17

按给出的层次结构模型，设为目标层A、准则层C（有k 个准则因素）、措施层P（有n个方案）。由决策者用其他方法给出各层因素之间的两两比较得出A-C 判断矩阵为：

然后分别给出Ci-P的判断矩阵（i＝1，2，…，k）。

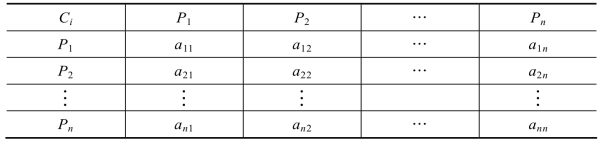
用近似法计算各判断矩阵的最大特征值和特征向量。

4.计算方法

一般来讲，在AHP 法中计算判断矩阵的最大特征值与特征向量，并不需要很高的精度，故用近似法计算即可。最简单的方法是求和法及其改进的方法，但方根法更好，这里只介绍方根法。

（1）方根法。

这是一种近似计算法，其计算步骤为：

① 计算判断矩阵每行所有元素的几何平均值：

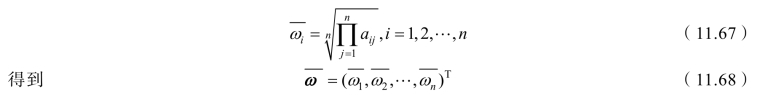
② 将归一化，即计算：

得到即所求特征向量的近似值，这也是各因素的相对权重。

③ 计算判断矩阵的最大特征值λmax：

其中为向量Aω的第i 个元素。

④ 计算判断矩阵的一致性指标，检验其一致性。

当各层次的诸因素的相对权重都得到后，进行措施层的组合权重计算。

（2）组合权重计算。

设有目标层A、准则层C、方案层P 构成的层次模型（当层次更多的模型，计算相同），目标层A 对准则层C的相对权重为：

准则层的各准则Ci，对方案层Pn个方案的相对权重为：

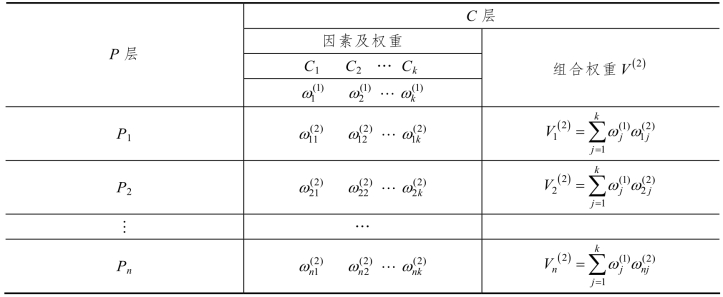
因此，各方案对目标而言，其相对权重是通过权重组合而得到的，其计算可采用表格式进行（见表11-26）。这时得到的为P 层各方案的相对权重。

表11-26　P 层各方案的相对权重