由定理4 可知,求矩阵对策解(x*,y*)的问题等价于求解不等式组(10.18)和(10.19);又由定理5 和定理6 可知,如果最优策略中的![]() 均不为零,则可将上述两不等式组的求解问题转化为下面的两个方程组的求解问题。
均不为零,则可将上述两不等式组的求解问题转化为下面的两个方程组的求解问题。
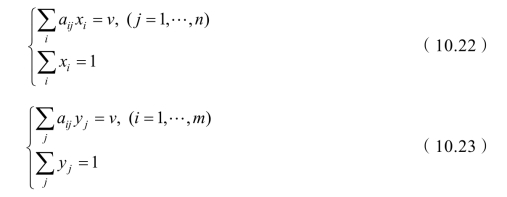
如果方程组(10.22)和(10.23)存在非负解x*和y*,便求得了对策的一个解。如果这两个方程组不存在非负解,则可视具体情况,将式(10.22)和式(10.23)中的某些等式改成不等式,继续试求解,直至求得对策的解。这种方法由于事先假定![]() 均不为零,故当最优策略的某些分量实际为零时,式(10.22)和式(10.23)可能无解,因此,这种方法在实际应用中有一定的局限性。但对于2×2的矩阵,当局中人Ⅰ的赢得矩阵
均不为零,故当最优策略的某些分量实际为零时,式(10.22)和式(10.23)可能无解,因此,这种方法在实际应用中有一定的局限性。但对于2×2的矩阵,当局中人Ⅰ的赢得矩阵
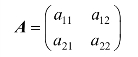
不存在鞍点时,容易证明,各局中人的最优混合策略![]() 均大于零。于是,由定理6,方程组
均大于零。于是,由定理6,方程组
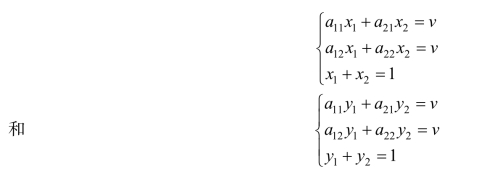
一定有严格的非负解(也就是两个局中人的最优策略):
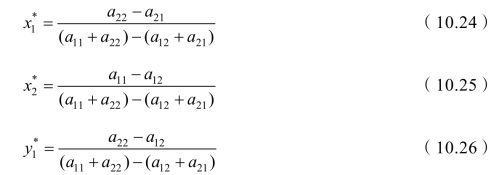
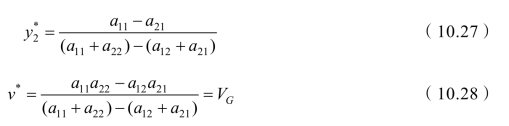
例10-13 求解矩阵对策G={S1,S2; A},其中A 为
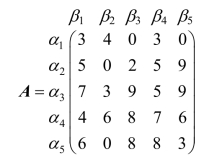
解 首先可利用矩阵对策的优超原则对矩阵A 进行化简。为此,应用优超原则依次简化得到A1,A2和A3:
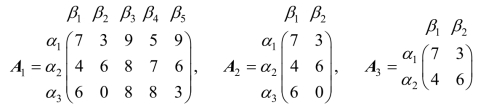
易知 A3没有鞍点。由定理6,可以求出方程组
 (https://www.xing528.com)
(https://www.xing528.com)
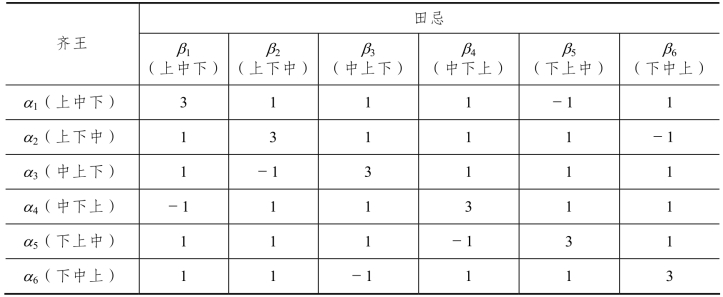
例10-14 求解矩阵对策“齐王赛马”。
战国时期,齐国国王有一天提出要与大将军田忌赛马。田忌答应后,双方约定:
(1)每人从上、中、下三个等级中各出一匹马,共出三匹;
(2)一共比赛三次,每一次比赛各出一匹马;
(3)每匹被选中的马都要参加比赛,而且只能参加一次;
(4)每次比赛后输者要付给胜者一千金。
当时在三个不同等级中,齐王的马都比田忌的马强些,看来,田忌要输三千金了,但由于田忌采用了谋士的意见,最终反败为胜。谋士的主意是:
(1)每次比赛前先让齐王说出他要出哪匹马;
(2)让田忌用其下马对齐王的上马;
(3)让田忌用其中马对齐王的下马;
(4)让田忌用其上马对齐王的中马。
解 根据上述对“齐王赛马”的描述和比赛规则,令齐王的赢得矩阵为A,并设齐王和田忌的最优混合策略分别为![]() 从而列出求解方程组,并求解得到
从而列出求解方程组,并求解得到
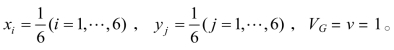 即双方都以
即双方都以![]() 的概率选取每个纯策略,或者说在六个纯策略中随机地选取一个为最优策略。总的结局应该是:齐王赢的机会为
的概率选取每个纯策略,或者说在六个纯策略中随机地选取一个为最优策略。总的结局应该是:齐王赢的机会为![]() 赢得的期望值是1 千金。但是,如果齐王在每出一匹马前将自己的选择告诉对方,即公开了自己的策略,如齐王的出马次序是(上,中,下),并且这个次序让田忌知道了,则田忌就可用(下,上,中)的出马次序对付之,结果是田忌反而赢得1 千金。因此,当矩阵对策不存在鞍点时,竞争的双方均应对每局对抗中自己将选取的策略加以保密,否则,策略被公开的一方是要吃亏的。
赢得的期望值是1 千金。但是,如果齐王在每出一匹马前将自己的选择告诉对方,即公开了自己的策略,如齐王的出马次序是(上,中,下),并且这个次序让田忌知道了,则田忌就可用(下,上,中)的出马次序对付之,结果是田忌反而赢得1 千金。因此,当矩阵对策不存在鞍点时,竞争的双方均应对每局对抗中自己将选取的策略加以保密,否则,策略被公开的一方是要吃亏的。
表10-3 “齐王赛马”时齐王在各局势的赢得表 单位:千金
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




