连续检查的（r，Q）存储模型：订货量与再订货点

（r，Q）存储模型是指在能够连续检查库存水平的前提下，当检查到库存量降低到r 时就订货，订货数量为Q。假设L 时间内的需求量x 为随机变量，其密度函数为f（x），单位时间需求量的期望值为D，订货提前时间 L（L＞0）为常数。若L 时间内的实际需求量超过r，则发生缺货现象，当到货后再满足这部分缺货。其中r 表示再订货点（reordering point），Q 表示订货量，因此，（r，Q）存储模型也称为订货量-再订货点模型。图9-7 描述了需求概率已知情况下的（r，Q）存储模型。可以看出，当Q 单位的产品到达时，库存会有一个大幅度的上涨；随后库存量以一个变动的速度下降，当降至再订货点r 时，会发出新的订单。

图9-7　模型七的存储示意图

由于单位时间需求量的期望值为D，每次的订货量为Q，则单位时间的订货次数期望值为所以单位时间订货费用为

从图9-7 可以看出，缺货情况可能出现在生产时间L 内，而这段时间开始有存货r，实际需求量为x，则有：当x≤r时，缺货量为零；当x＞r时，缺货量为（x-r）。因此，在任一周期内出现缺货的期望值为单位时间内周期数的期望值为则缺货费用的期望值为

同前面的模型分析一致，假设库存系统的输出是均匀变化的，L 时间内需求量的期望值为LD，剩余存储量为r-LD，则周期内的平均存储量为因此单位时间内存储费用的期望值为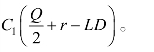

因此，单位时间内总费用的期望值为

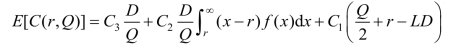
将上式分别对r 和Q 求偏导，并令其等于零，可得

显然，直接通过上述两式求解很困难，可以采取主次迭代法求解，这里不做深入讨论。(www.xing528.com)

例9-10　M 汽车销售公司是M 牌汽车销售代理商，每次的订货提前期L 为常数。有关资料如下：

每辆汽车一年的持有成本（存储费、保养费、利息等）是2000 元。

每次订货准备成本（订货手续费、运费等）是500 元。

缺货时顾客愿意延期提货的占80%，这时公司给予价格优惠，利润损失为1000 元；缺货时顾客放弃购买的占20%，公司利润损失为6000 元。

已知年销售量是[0，1200]上的均匀分布，提前期为常数10 天，求（r，Q）策略。

解　由题意可知

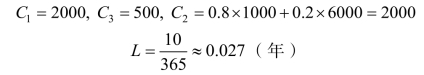
又由题意可知，年销售量是[0，1200]上的均匀分布，故年平均需求量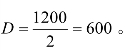从而提前期内的平均需求量为DL=600×0.027=16.2≈16；需求量的概率密度函数为

将 r（1）=31.47迭代，依次得到

Q（2）=17.7768，r（2）=31.45；Q（3）=17.8007，r（3）=31.44；…，Q（5）=17.802，r（5）=31.44可以认为Q≈18，s≈31。则安全库存为r=s-D（L）=31-16=15。故（r，Q）策略为（15，18）。