随机需求下的离散报童问题，最优解Q*=4台

1.报童问题分析方法Ⅰ

例9-4（报童问题） 某报童每天需要销售一定数量的报纸，其售报数量是一个随机变量。报童每售出一份报纸可赚k 元，若报纸未售出，每份赔h 元。每日售出报纸份数r的概率 P（r）是已知的，问该报童每日最好准备多少份报纸可使利润最大？

解　设某报纸的日需求量为r，报童的订货量为Q，先计算报童的利润期望值。

当需求量不超过订货量，即r≤Q时，报童只能售出r 份，滞销（Q-r）份，因此利润为

由于需求量r 是随机变量，因此，利润期望值为

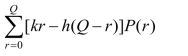
当需求量大于订货量，即r＞Q时，报童只有Q 份可供销售，因此利润为kQ，其期望值是

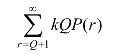
因此，总的利润期望值是

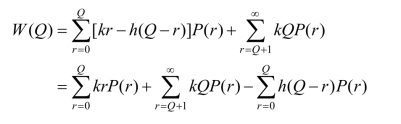
由于这是离散的变量，无法通过求导数得到最优订货量，可通过边际分析法来求解。设最大利润期望的订货量为Q*，应满足如下两个条件：

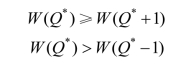
由第一个条件可得

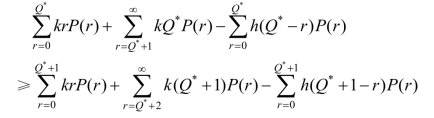
经简化后得

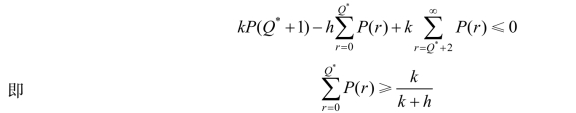
同理从第二个条件可得

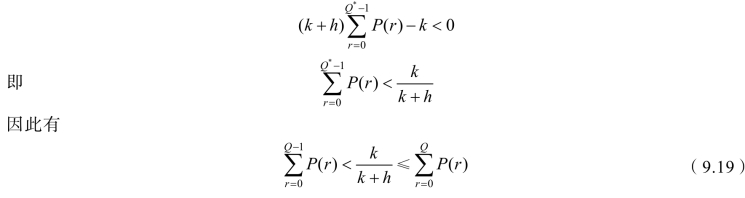
故模型六的最佳订货量 Q*可由式（9.19）确定。

例9-5　某报亭营业主每天销售的报纸数量是随机的，每千张报纸可获利7 元，如果当天卖不出去，则每千张报纸赔4 元。根据报亭营业主以前的销售经验，每天售出报纸数量r的概率如表9-2 所示，问每天应进多少张报纸？

表9-2　每天售出报纸数量r的概率

解　由题意可知k=7，h=4，则

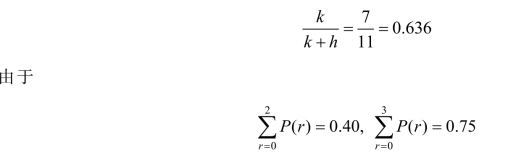
所以，Q*=3千张时利润期望值最大。

报童问题是离散型随机需求存储问题的典型问题，前面已根据最大利润期望值法获得了最优解条件。除此之外，也可以用最小损失期望值法得到相同的最优解条件。

设单位进货过量的单位损失是r，进货不足造成的单位损失为h（一般为售出一份的利润），那么：

当r≤Q时的滞销期望损失是

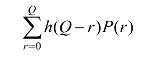
当r＞Q时的缺货期望损失是

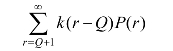
因此，总的期望损失为

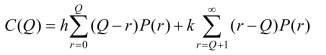
根据边际分析不等式(www.xing528.com)

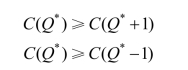
再用最大利润期望值法相同的分析可得如下的最优解条件：

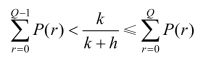
可见，与由最大利润期望值法得到的最优解条件相同。事实上，不难得到：

例9-6　某超市拟销售某进口奶制品，该奶制品的进价为50 元/件，售价为70 元；由于奶制品的保质期较短，若当天售不完，则第二天必须减价为40 元才能售出。已知售货量r 服从泊松分布其中λ=6是平均售货数，问该店应订购该商品多少？

解　由题意知k=20，h=10。首先计算

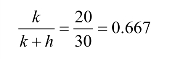
因为λ=6，令

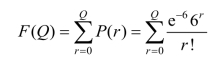
查表得 F（6）=0.606，F（7）=0.744。由于所以最佳订货量应为7 件，此时的期望损失值最小。

例9-7　某汽车厂商拟在一展销会上出售一批汽车。每出售一台可盈利8 万元。若展销会结束时未售出的汽车必须降价处理，且每台亏损1 万元，问该汽车厂应准备多少台汽车？已知汽车在展销会上售出的概率如表9-3 所示。

表9-3　汽车销售量及概率

解　这是一个需求为离散变量的单周期随机存储问题，由

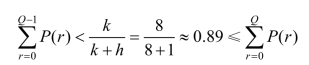
计算得到 Q*=4台，即该厂应准备4 台汽车参展。

2.报童模型的分析方法Ⅱ

报童订货时，若订得太多，因卖不掉会受到亏损；但若订得太少，由于不够卖也会因缺货而损失可得的利润。因此，当订货量逐渐增多，且增加到n 件时，由于

故这个点称为边际平衡点（point of marginal equilibrium）。平衡点所对应的量则为总利润最高时的订货量。

假设k 为若第n 件被卖掉，此时所得的利润；h 为若第n 件卖不掉，此时的损失，当需求量随机时，可用概率表示平衡点的条件：

其中P 是第n 件被卖掉的概率，1-P是第n 件卖不掉的概率。解上式可得

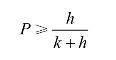
可由此确定最佳订货量n。

例9-8　A 产品每件销售价为100 元/件，每件成本70 元；如果卖不掉还有残值30 元。在这一时期需求量在35～40（件），即35 件以下全部可以卖掉，超过40 件则卖不掉。需求概率以及与此关联的可销售出的概率如表9-4 所示。

表9-4　需求概率以及与此关联的可销售出的概率

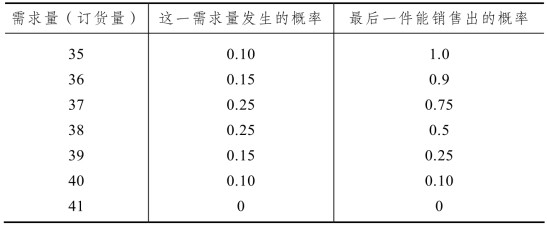
解　根据题意，最后一件销售出去的概率为1-P（需求 ＜ n）。当需求在35 件或以下，备货35 件时，最后一件卖掉的概率一定是1；当备货量是36 件时，最后一件卖掉的概率是除去需求为35的概率0.1，即0.9。以此类推。

本例中，每销售一件，可得利润k=100-70=30元；否则积压一件，其损失为h=70-30=40元。于是根据以上公式有

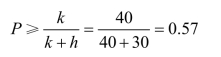
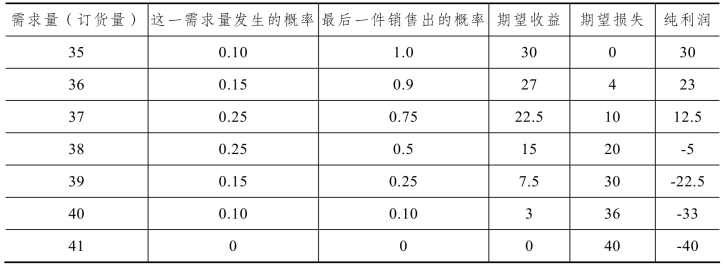
查表9-4 可得：当n=37件时，其最后一件销售出的概率P=0.75＞0.57。故进货37 件为最佳。由表9-5 不难看出，不同进货量下的盈亏状况。因此，可以确定37 件进货量是盈亏平衡点。

表9-5　期望盈利/亏损表