【摘要】：图9-4模型二的存储示意图其中，最大存储量＝最大订购量，即Q；订货周期为t；边订货边销售期为T，存储期为t-T。事实上，在该模型中，变量并没有增加，独立变量只有一个。因此，可以说模型一是模型二的特例，模型二是模型一的扩展。例9-2某汽车公司每月汽车底盘的需求量为100 件，每月的生产量为500 个，每批装配费为5 元，每月每辆汽车底盘的存储费为0.4 元。
假设需求是连续均匀，需求速度R 是常数，库存的补货需要时间，补货速度（或生产速度）为P，同时为了使讨论有意义，应有P＞R。此时的存储状态如图9-4 所示。
图9-4 模型二的存储示意图
其中，最大存储量＝最大订购量，即Q；订货周期为t；边订货边销售期为T，存储期为t-T。则有
T 与t的关系由（P-R）T=R（t-T）知
这意味着在T 时间内订货的产品要足够满足在t 时间内的消耗。事实上，在该模型中，变量并没有增加，独立变量只有一个。
t 时间内的平均费用＝存储费+调整费，即 C（t）为
(www.xing528.com)
对t 求导数得最佳订货周期：
每次最佳订货批量：
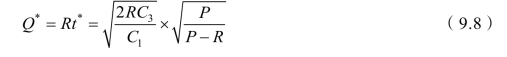
与模型一相比，模型二的t*和 Q*仅差一个系数
而当P →∞时，此系数等于1，即两模型的结果完全相同。因此，可以说模型一是模型二的特例，模型二是模型一的扩展。
例9-2 某汽车公司每月汽车底盘的需求量为100 件，每月的生产量为500 个，每批装配费为5 元，每月每辆汽车底盘的存储费为0.4 元。问：应如何安排生产才能使总费用最少？
解 依题意可知，C3=5，C1=0.4，P=500，R=100，根据式（9.5），最佳生产量为
最佳的生产周期为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
