不允许缺货，备货时间很短的基本EOQ模型解析

在研究、建立模型时，需要做一些假设，目的是使模型简单、易于理解、便于计算。为此做如下假设：

（1）缺货费用无穷大；

（2）当存储降至零时，可以立即得到补充（即备货时间或拖后时间很短，可以近似地看作零）；

（3）需求是连续的、均匀的，设需求速度R（单位时间的需求量）为常数，则t 时间的需求量为Rt ；

（4）每次订货量不变，订购费不变（每次备货量不变，装配费不变）；

（5）单位存储费不变。

因此，在T 时间内的存储模式可用图9-2 表示。

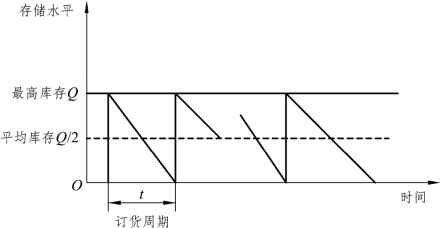
图9-2　基本EOQ 模型的存储示意图

为方便分析，假设单位货物存储费为C1，单位货物缺货损失为C2，每次的订货费用为C3，货物单价为K，订货周期为t，每次补货量为Q。Q 需要满足t 时间的市场需求，因此Q=Rt。t 时间内的平均存储量为

t 时间内的平均订货费为

由图9-2 可知，在订货周期t 内的存储量为一个三角形的面积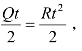因此，t 时间内的平均存储量为t 时间内的平均存储费为

t 时间内的平均总费用 C（t）等于平均存储费和平均订货费之和，即有(www.xing528.com)

其中，第一项是存储费用，时间越长，该项费用越大，因此，从存储费用看，每次应当尽量少购一点；第二项是订货费，它与订货量无关，因此，订货量越大（可用时间越长），单位货物费用越少，从这一点上说应当每次尽量多购一些。

在平均总费用 C（t）中，由于KR 为常数，与最优的订货策略无关，所以一般在分析中常不考虑这一项费用。因此，求解的目标函数变为

最优的存储策略是选择最优订货周期和最优订货量以使平均总费用最少。存储费用、缺货费用和采购费用之间的关系可用图9-3 表示。

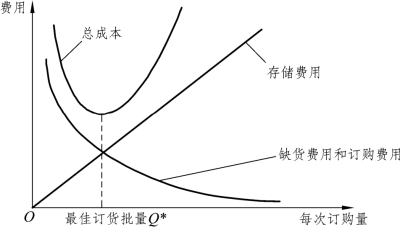
图9-3　存储费用、缺货费用和采购费用之间的关系

根据微积分求极值的方法，我们将 C（t）对t 求一阶导数，并令其为零，即有

这便是存储论中著名的经济订货批量公式，简称经济批量公式或EOQ 公式。这样得到的最少平均费用（不包括KR）为

例9-1　某医院药房平均每年需购入某种药1600 瓶，每瓶药品的订货费为5 元，每次药品到达后先存入仓库，每瓶药品的每月保管费为0.1 元。试求医院对改药品的最佳订货批量。

解　已知R=1600，C1=0.1，C3=5，由式（9.5）得最佳订货批量：

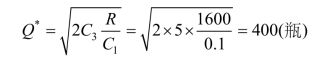
故医院每次应订货400 瓶最为经济合理。