时间-费用优化：增加费用缩短工期，节省总费用1600元！

绘制网络计划图时，要研究如何使完成项目的工期尽可能地缩短，费用尽可能地减少；或在保证既定项目完成时间条件下，所需要的费用最少；或在费用限制条件下，项目完工的时间最短。这就是时间-费用优化要解决的问题。完成一项目的费用可以分为两大类：

（1）直接费用。直接与项目的规模有关的费用，包括材料费用、直接生产工人工资等。为了缩短工作的持续时间和工期，需要增加投入，即增加直接费用。

（2）间接费用。间接费用包括管理费等。一般按项目工期长度进行分摊，工期愈短，分摊的间接费用愈少。

一般项目的总费用与直接费用、间接费用、项目工期之间存在一定的关系，可以用图7-10表示，图中：T1为最短工期，项目总费用最高；T2为最佳工期；T3为正常工期。当总费用最少工期短于要求工期时，就是最佳工期。

图7-10　工期与总费用的关系曲线

进行时间-费用优化时，首先要计算出不同工期下的最低直接费用率，然后考虑相应的间接费用。费用优化的步骤如下：

（1）计算工作费用增加率（简称费用率）。

费用增加率是指缩短工作持续时间每一单位时间（如一天）所需要增加的费用。

按工作的正常持续时间计算各关键工作的费用率，通常可表示为

其中ΔCi-j为工作i-j的费用率；CCi-j为将工作i-j持续时间缩短为最短持续时间后，完成该工作所需要的直接费用；CNi-j为在正常条件下完成工作i-j所需要的直接费用；DNi-j为工作i-j正常持续时间；DCi-j为工作i-j最短持续时间。

（2）在网络计划图中找出费用率最低的一项关键工作或一组关键工作作为缩短持续时间的对象。其缩短后的值不能小于最短持续时间，不能称为非关键工作。(www.xing528.com)

（3）在计算相应增加的总费用的同时，考虑由于工期缩短致使间接费用的变化，并在此基础上计算项目的总费用。

重复以上步骤，直到获得满意的方案为止。

下面通过例子来说明。已知项目的每天间接费用为400 元，利用表7-6中的已知资料，按图7-7 安排进度，项目正常工期为170 天，对应的项目直接费用为68900 元，间接费用为170×400＝68000 元，项目总费用为136900 元。这是在正常条件下进行的方案，称为170 天方案。若要缩短此方案的工期，首先缩短关键路线上直接费用率最小的工作的持续时间，在170 天方案中，关键工作K，G的直接费用率最低，从表中可见这两项工作的持续时间都只能缩短10 天。由此总工期可以缩短到170-10-10＝150 天。按150 天工期计算，这时总直接费用增加到68900+（290×10+350×10）＝75300 元。由于缩短工期，可以减少间接费用400×20＝8000 元，故工期为150 天方案的总费用为75300+60000＝135300 元。与工期170 天方案相比，可以节省总费用1600 元。

但在150 天方案中已有两个关键路线，即

如果再缩短工期，工作的直接费用将大幅度增加。例如，在150 天方案的基础上再缩短工期10 天，称为140 天方案。这时应选择工作D，缩短10 天；工作H 缩短5 天（只能缩短5 天），工作E 缩短5 天。这时，直接费用变为75300+400×10+400×5+500×5＝83800 元，间接费用为140×400＝56000 元，总费用为139800 元。显然，140 天方案的总费用比150 天方案和170天方案的总费用都高。综合考虑，150 天方案为最佳方案，计算结果汇总在表7-7中。

表7-6

续表

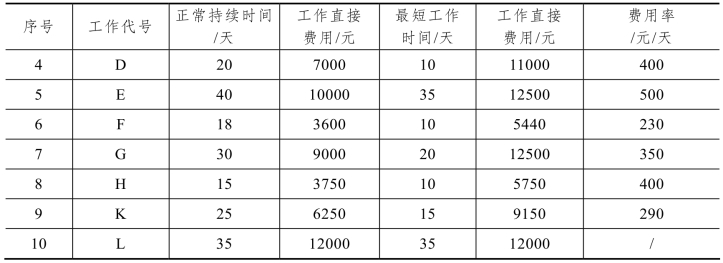
表7-7