计算关系式并应用于网络计划图中的时间参数计算与填写

这些时间参数的关系以及工作的关系状态可以用图7-6 表示。手工计算可在网络图上进行，计算步骤为：

（1）计算各路线的持续时间（见表7-2）。

（2）按网络图的箭线方向，从起始工作开始，计算各工作的ES，EF。

（3）从网络图的终点节点开始，按逆箭线的方向，推算出各工作的LS，LF。

（4）确定关键路线（CP）。

（5）计算TF 和EF。

（6）平衡资源。

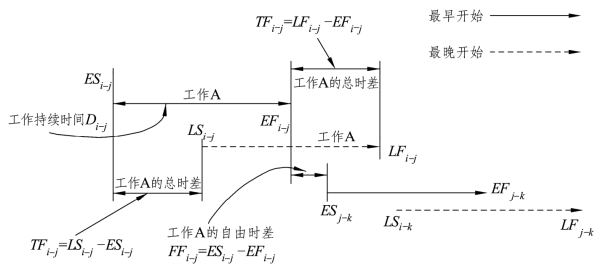
图7-6

例7-2　计算各工作的时间参数，并将计算结果记入网络计划图的相应工作的格子中，如图7-7 所示。

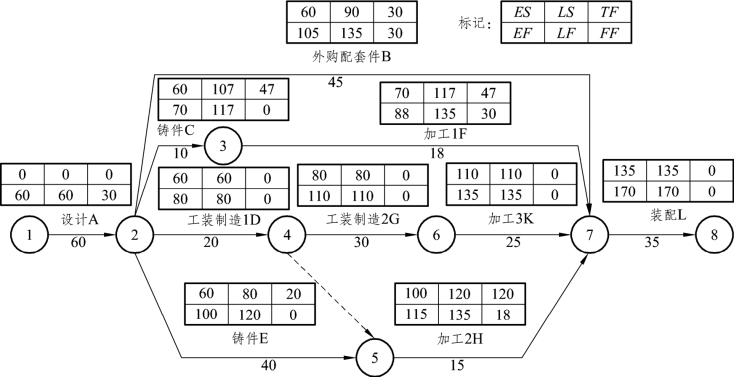
图7-7

（1）工作最早开始时间ES 和工作最早完成时间EF的计算。

利用网络计划图，从网络计划图的起始点开始，沿箭线方向依次逐项计算。第一项工作的最早开始时间为0，记作ESi-j=0（起始点i=1）；第一项工作的最早完成时间EF1-j=ES1-j+D1-j。第一项工作完成后，其紧后工作才能开始，故其工作的最早完成时间EF就是其紧后工作的最早开始时间ES。本工作的持续时间为D 表示为：

计算工作的ES 时，在有多项紧前工作情况下，只能在这些紧前工作都完成后才能开始。因此，本工作的最早开始时间是：

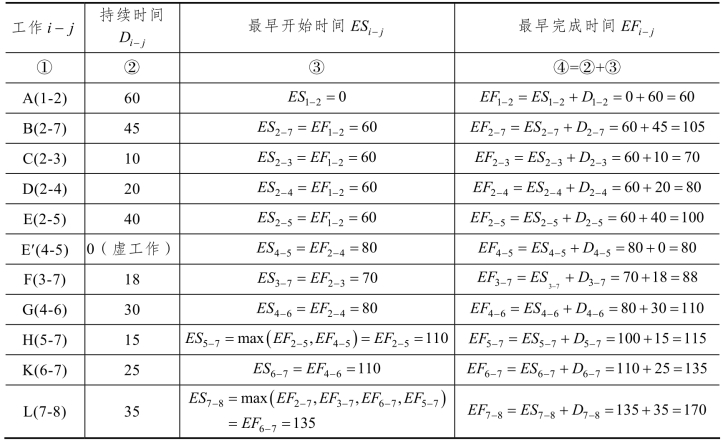
例7-1的ES，EF的计算值在表7-3的③，④列中。

表7-3

(www.xing528.com)

利用双代号的特征，很容易在表中确定某工作的紧前工作和紧后工作。凡是后续工作的箭尾代号与某工作的箭头代号相同者，都是它的紧后工作；凡是现行工作的箭头代号与某工作的箭尾代号相同者，都是它的紧前工作。在表7-3中首先填入①，②两列数据，然后由上往下计算ES 与EF。若某工作（i-j）的先行工作中存在几个（h-i），从中选择最大的EFh-i来计算ESi-j=maxh[EFh-i]，即计算EFi-j。例如，计算ES7-8时，可从表7-3的④列已有的EF6-7，EF5-7，EF3-7中找到最大的EF6-7=135，将它填入表7-3的③列，对应的L（7-8）行即可。

（2）工作最迟开始时间LS 与工作最迟完成时间LF 。

利用网络计划图，从网络图的终点节点开始，采用逆序法逐项计算。即按逆箭线方向，依次计算各工作的最迟完成时间LF 和最迟开始时间LS，直到第一项工作位置。网络图中最后一项工作（i-n）（j=n）的最迟完成时间应由工程的计划工期确定；在未给定时，可令其等于其最早完成时间，即LFi-n=EFi-n。EFi-n由表7-3中的计算结果得知，并且应当小于或等于计划工期规定的时间 Tr。

其他工作的最迟开始时间LSi-j=LFi-j-Di-j；当有多个紧后工作时，最迟完成时间

其计算可在表7-4中进行。计算时从下到上进行，即从工作（7-8）开始，令表7-4的⑤列最后一行LF7-8=EF7-8=170。

表7-4

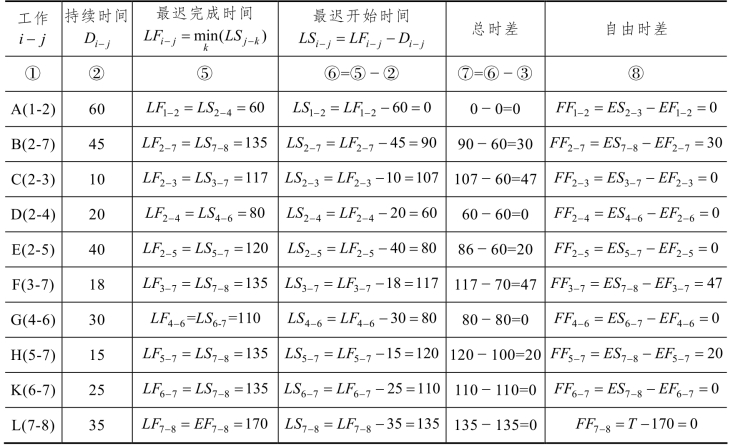
于是可计算出EF7-8=LF7-8-D7-8=135。工作L（7-8）的紧前工作的箭尾代号与工作L（7-8）的箭头代号是相同的，这里有K（6-7），H（5-7），F（3-7），B（2-7）；它们只有唯一的紧后工作L（7-8），所以LF6-7，LF5-7，LF3-7，LF2-7都等于LF7-8=135。填入表7-4⑤列的相应行即可。当具有多个紧后工作时，如要计算LF1-2时，先查A（1-2）的紧后工作有几个，从代号可以看到是B（2-7），C（2-3），D（2-4），E（2-5），对应的有LS2-7=90，LS2-3=107，LS2-4=60，LS2-5=80。其中最小的是60，即LF1-2=LS2-4=60。

（3）工作时差。

工作时差是指工作有机动时间，常有两种时差，即工作总时差和工作自由时差。

① 工作总时差TFi-j。

TFi-j是指在不影响工期的前提下，工作所具有的机动时间，按工作计算法计算。在表7-4中参见⑦=⑥-③的数据。即

② 工作自由时差FF。

工作自由时差是指，在不影响其紧后工作最早开始的前提下，工作所具有的机动时间。

计算结果见表7-4⑧和图7-7。工作自由时差是某项工作单独拥有的机动时间，其大小不受其他工作机动时间的影响。

下面介绍关键路线的特征：在线路上从起点到终点都由关键工作组成。在确定型网络计划中是指线路中工作总持续时间最长的线路；在关键线路上无机动时间，工作总时差为零。在非确定型网络计划中是指估计工期完成可能性最小的线路。