解决BMZ公司的最大流问题：从斯特加特工厂到洛杉矶配送中心的配件流

1.背景

BMZ 公司是欧洲一家生产豪华汽车的制造商，它生产的汽车虽然在发达国家的销量不错，但对于这家公司来说，出口到美国显得尤其重要。

BMZ 公司因为提供优质的服务而获得良好的声誉。它能够保持这个声誉的一个很重要的秘诀就是它有着充裕的汽车配件供应，从而能够随时给公司众多的经销商和授权维修店供货。这些配件主要存放在公司的配送中心里，一旦有需求就可以立即送货。卡尔·斯密特（供应链经理）需要优先考虑的是避免这些配送中心发生短缺状况。

该公司在美国有几个配送中心，但是，离洛杉矶中心最近的一个配送中心却坐落在离洛杉矶1000 多英里的西雅图。由于BMZ 公司的汽车在加利福尼亚越来越受欢迎，所以保证洛杉矶中心良好的供应就显得尤为重要了，然而，现在洛杉矶的供应量不断减少的现状却成为该公司高层管理者真正关心的问题，正如现在卡尔深切体会到的那样。

该公司的大部分汽车配件是在该公司坐落于德国斯图加特的总厂和新车一起生产的，也正是这家工厂向洛杉矶中心供应汽车配件。由于其中的一些配件体积很大，而且有些配件的需求量很大，这就使得汽车配件供应的总量非常庞大，每月要运送超过30 万立方英尺的配件，而下个月需要更多的配件以补充正在减少的库存。

2.问题

卡尔需要尽快地制订一个方案，使得下个月从总厂运送到洛杉矶配送中心的供应件尽可能地多。他已经认识到这是个最大流问题，即使得从总厂运送到洛杉矶配送中心的配件流最大的问题。由于总厂生产的配件量远远大于能够运送到配送中心的量，所以可以运送配件数量的上限就是该公司配送网络的容量。

这个配送网络如图6-44 所示。在图中，标有ST 和LA的节点分别代表斯图加特的工厂和洛杉矶的配送中心。由于工厂所在地有一个铁路转运点，所以首先要通过铁路运输把配件运送到欧洲的三个港口：鹿特丹（节点RO）、波尔多（节点BO）和里斯本（节点LI）；然后通过船运把它们送到美国的港口纽约（节点NY）或新奥尔良（节点NO）；最后用卡车把它们从港口运送到洛杉矶的配送中心。

然而经营这些铁路、船舶和卡车的组织是独立的公司，这些公司又为很多的公司运输货物，加上对这些老主顾原先的承诺，所以这些公司不可以在短时间内为任何一个客户大量增加运输空间配额。因此，BMZ 公司只能够保证获得下个月每条运输航线有限的运输空间。图6-44 已经给出可以获得的空间数量，以100 立方米为1 个单位（100 立方米约为3500 立方英尺，因此需要运送的货物体积很大）。

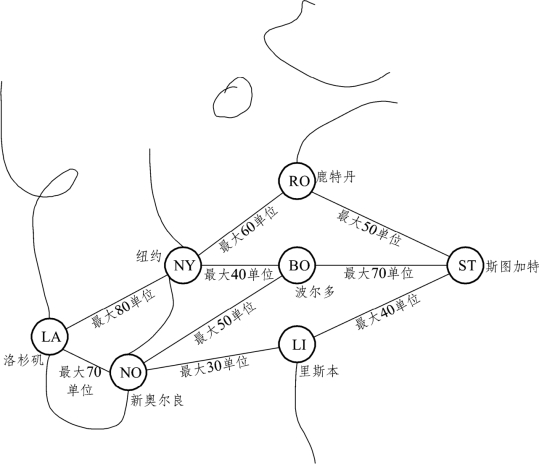
图6-44　BMZ 公司从德国斯特加特的工厂到杉矶的配送中心的配送网络

3.模型描述

图6-45 是这个最大流问题的网络模型。这个网络没有显示该配送网络具体的地理分布，而是简单地把各节点（代表不同的城市）均匀地排成几列。节点间的弧代表运输路线，每条弧的容量（弧下方括号内的数字）代表在这条运输路线上所能得到的运输空间的数量。这个问题的目标是确定通过每一条弧发送多少流量（即通过每条运输路线可以运送多少单元的货物），使得从斯阁加特工厂到洛杉矶配送中心的运输单位总量最大。

(www.xing528.com)

图6-45

图6-46 给出了该问题的电子表格模型。其中，目标单元格MaxFlow（D14）中的数据是从斯图加特到洛杉矶总流量的单位数。图的下方给出的公式包括D14=I14，其中I4 给出了从斯图加特到洛杉矶的净流量。NetFlow（I4：I10）的公式同样使用了两个SUMIF 函数的差来计算每个节点产生的净流量。因为目标是使MaxFlow（D14）的值最大化，所以在Solver对话框指出这个目标单元格的数据要达到最大。点击Solve 按钮，在可变单元格Ship（D4：D12）中就得到了BMZ 公司通过各条线路应该运输多少数量的最优解。

图6-46

但是，卡尔对这个解还不是十分满意。在柏林，即斯图加特的工厂的北面，公司有一家较小一点的工厂也生产汽车配件。虽然这家工厂通常用来给北欧、加拿大和美国北部地区的配送中心（包括西雅图的一个）协助供货，但是它也同样可以运输配件到洛杉矶的配送中心去。而且，当洛杉矶配送中心出现库存短缺时，西雅图的配送中心有能力供应配件给洛杉矶配送中心的客户。

受到这一点的启发，卡尔为解决当前洛杉矶存货短缺的问题开发了一个更好的方案，即与其仅仅使从斯图加特的工厂到洛杉矶配送中心的运瑜量最大，不如使得两个工厂到洛杉矶和西雅图这两个配送中心的运输量最大。

图6-47 显示的网络模型代表扩展后的配送网络，这个经过扩展的网络包括两个工厂和两个配送中心。除了图6-44 和图6-45的节点以外，节点BE 代表位于柏林的较小的工厂，节点HA 和节点BN 分别代表为这家工厂提供服务的汉堡和波士顿的另外两个港口。和以前一样，弧代表运输路线，每一条弧下方括号里的数字代表该弧的容量，即下个月可以通过这条运输路线的最大运输单位数。

图6-47

对应的电子表格模型如图6-48 所示，所用的格式和图6-46 是一样的。但是，现在目标单元格 MaxFlow（D21）得到的数据是从斯图加特和柏林这两个工厂运出的总流量，所以D21=I4+I5。图6-48中的可变单元格Ship（D4：D19）中显示的是下个月通过各条运输路线运送数量的最优解。把这个解和在图6-46中得到的解相比较，我们可以看到卡尔扩展配送网络（使其包含第二个工厂和西雅图配送中心）所产生的影响。正如在两张图中的I 列所显示的那样，运送到洛杉矶的单位数由150 增长到了160，再加上60 单位运到西雅图作为洛杉矶库短缺的备份，这个方案不但解决了洛杉矶的危机，而且也使卡尔赢得了高层管理者的称赞。

图6-48

BMZ 公司问题扩展后作为最大流问题变形的电子表格模型。